nLab singular cohesion

Idea

What is called singular cohesion in SaSc 2020, following observations in Rezk 2014, is a form of cohesion on $\infty$-toposes which enhances any base notion of “smooth” cohesive geometry to a “singular-smooth” cohesive geometry which reflects the possible presence of orbi-singularities.

For example, where smooth manifolds are faithfully embedded into the cohesive $\infty$-topos of smooth $\infty$-groupoids, so their orbifolds are faithfully embedded among singular-smooth $\infty$-groupoids such that, for global quotient orbifolds, their cohesive shape is the homotopy type of the underlying G-spaces in proper equivariant homotopy theory.

For the base $\infty$-topos $Grpd_\infty$, embodying plain homotopy theory, its singular-cohesive enhancement is global equivariant homotopy theory and hence every singular-cohesive $\infty$-topos is cohesive over (in particular) global equivariant homotopy theory, hence may be thought of as embodying a “globally equivariant and cohesive” homotopy theory.

In fact, every slice of a singular-cohesive $\infty$-topos over the canonical $G$-orbi-singularity $\boxed{\prec}\mathbf{B}G$ is cohesive over the $G$-equivariant homotopy theory over the given smooth cohesive base, with the inverse image of the cohesive geometric morphism being the embedding of cohesive $G$-orbispaces.

Globally equivariant geometric homotopy theory

Consider the full sub-$\infty$-category of $Grp_\infty$ on the connected, 1-truncated $\pi$-finite homotopy types

(1)$$\array{ Singularities &\coloneqq& Grpd^{fin}_{1, \geq 1} &\xhookrightarrow{\;}& Grp_\infty \\ \boxed{\prec}\mathbf{B}G & \mapsto & B G }$$

(sometimes called the “global orbit category”), hence the full sub (2,1)-category of groupoids on the delooping groupoids of finite groups $G$.

Then for $\mathbf{H}_{\subset}$ any base $\infty$-topos, the $\infty$-category of $\infty$-presheaves over $Singularities$ (1)

$$\mathbf{H} \,\coloneqq\, Glo \mathbf{H}_{\subset} \;\coloneqq\; PSh_\infty \big( Singularities \,, \mathbf{H}_{\subset} \big) \,,$$

which may be called the globally equivariant homotopy theory over the geometric homotopy theory $\mathbf{H}_{\subset}$, is cohesive over $\mathbf{H}_{\subset}$ (as is any $\infty$-presheaf $\infty$-topos over an $\infty$-site with a terminal object, see e.g. at adjoint quadruple the section Cohesion).

In fact, for any $\boxed{\prec}\mathbf{B}G \,\in\, Singularities$, the slice $\infty$-topos $Glo(\mathbf{H}_{\subset})_{/\boxed{\prec}\mathbf{B}G}$ is cohesive over the $G$-equivariant homotopy theory, hence over the $\infty$-topos of $\infty$-presheaves over the actual orbit category of $G$:

$$G \mathbf{H}_{\subset} \;\coloneqq\; Psh_\infty \big( G Orbits ,\, \mathbf{H}_{\subset} \big) \,.$$

For the discrete equivariance groups considered here, this follows on general abstract grounds (see at Adjoint quadruple – Cohesion) from the full sub (2,1)-category inclusion

$$\Singularities_{/\boxed{\prec}\mathbf{B}G} \underoverset {\hookleftarrow} {\overset{\tau_0}{\longrightarrow}} {\;\;\; \bot \;\;\;} G Orbits \,,$$

as discussed at cohesion of global- over G-equivariant homotopy theory (highlighted in Rezk 2014, Sec. 7).

Globally equivariant cohesive homotopy theory

This means that if $\mathbf{H}_{\subset}$ is itself cohesive over $Grpd_\infty$ then $\mathbf{H} = Glo(\mathbf{H}_{\subset})$ carries the following system of adjoint quadruples:

From SaSc 21

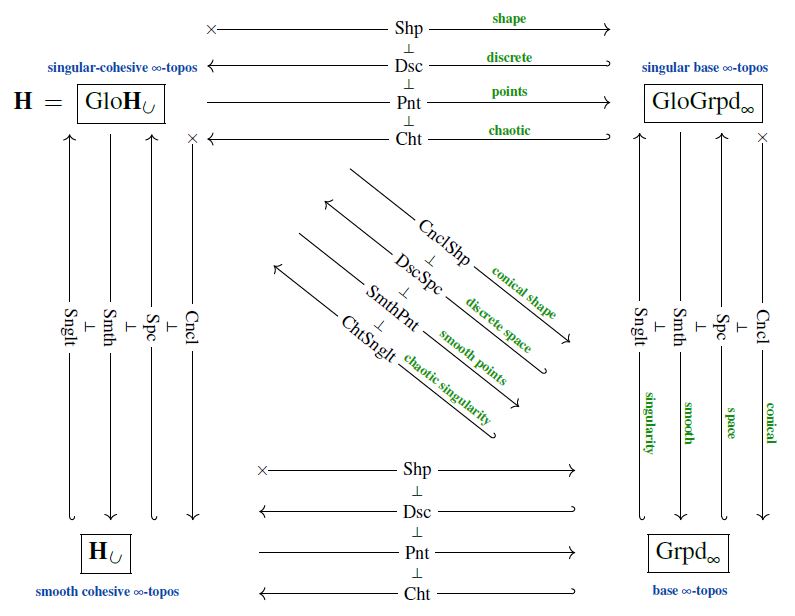
Singular cohesion

From this is obtained, in particular, a pair of adjoint triples of adjoint modalities on $\mathbf{H} \,\coloneqq\, Glo(\mathbf{H}_{\subset})$ which jointly reflect that its objects are geometric homotopy types whose geometric nature is “cohesive with orbi-singularities”:

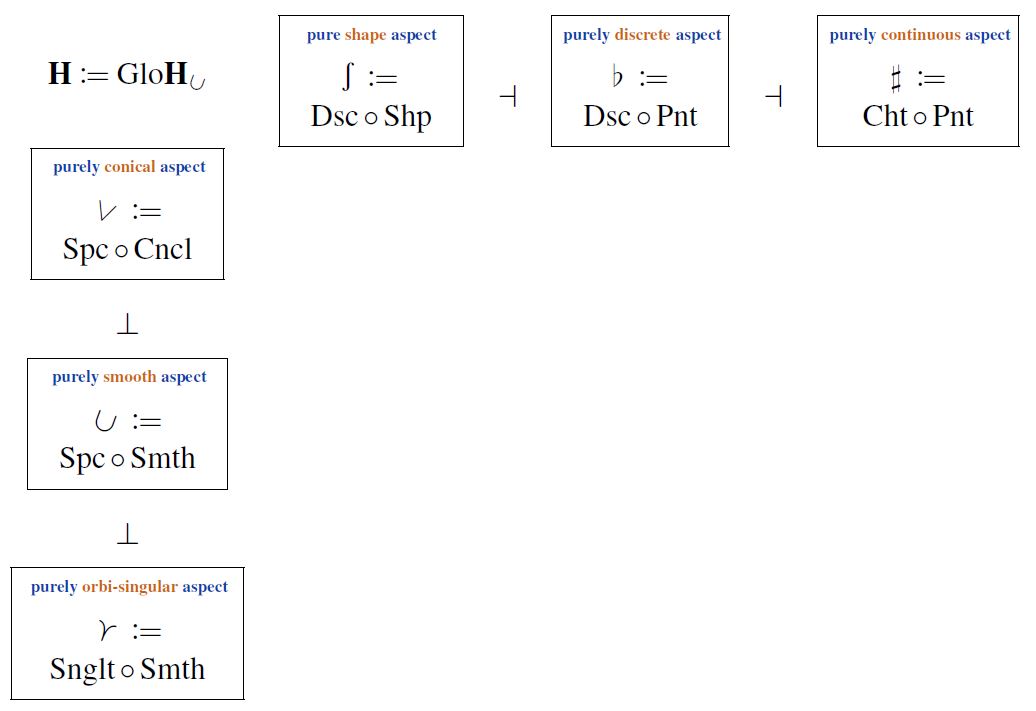
Orbifolds among singular-smooth $\infty$-groupoids

For example, when $\mathbf{H}_{\subset} \,=\,$ $SmthGrpd_\infty$, containing diffeological spaces as the full sub-$\infty$-category of 0-truncated concrete objects

$$DiffSpc \xhookrightarrow{ i_{\tau_0, \sharp_1} } SmthGrpd_\infty \,,$$

then the singular-cohesive $\infty$-topos $\mathbf{H} \,\coloneqq\, Glo(SmthGrpd_\infty)$ of singular-smooth $\infty$-groupoids contains diffeological orbifolds as a full sub (2,1)-category of orbi-singular-, hence of $\boxed{\prec}$-modal objects

$$\array{ DiffOrbfld &\xhookrightarrow{\;}& LieGrpd &\xhookrightarrow{ \;}& Glo(SmthGrpd_\infty) \\ && X \sslash G &\mapsto& \boxed{\prec}(X \sslash G) \mathrlap{\,,} }$$

and in such a way that their shape

$$\esh \, \prec \, (X \!\sslash\! G) \;\;\in\;\; G Grpd_\infty \xhookrightarrow{ Dsc } (G SmthGrpd_\infty)_{/\boxed{\prec}\mathbf{B}G} \xhookrightarrow{ G Spc } \mathbf{H}_{/\boxed{\prec}\mathbf{B}G}$$

is the incarnation of the D-topological space underlying $X$ as a G-space in $G$-equivariant homotopy theory (via Elmendorf's theorem).

Related concepts

• orbifold cohomology

• equivariant homotopy theory

  • globally equivariant homotopy theory

  • cohesion of global- over G-equivariant homotopy theory

References

The cohesion of global- over G-equivariant homotopy theory was first observed in

• Charles Rezk, Global Homotopy Theory and Cohesion, 2014 (pdf, pdf)

with emphasis on characterization of the full image under $G Spc$ of orbispaces in sliced global homotopy theory.

The above combination with smooth cohesion to singular cohesion was considered in

• Hisham Sati, Urs Schreiber, Proper Orbifold Cohomology (arXiv:2008.01101)

in discussion of orbifold cohomology, where the above notation is taken from, and in

• Hisham Sati, Urs Schreiber, Equivariant principal $\infty$-bundles

in discussion of equivariant principal $\infty$-bundles, where the above diagrams are taken from.