nLab finite rotation group

Idea

By a finite rotation group one means a finite subgroup of a group of rotations, hence of a special orthogonal group $SO(n)$ or spin group $Spin(n)$ or similar.

The finite subgroups of SO(3) and SU(2) follow an ADE classification (theorem below).

Classifications

Finite subgroups of $O(3)$, $SO(3)$ and $Spin(3)$

Theorem

(ADE classification of finite subgroups of SO(3) and Spin(3)$\simeq$ SU(2))

The finite subgroups of the special orthogonal group $SO(3)$ as well as the finite subgroups of the special unitary group SU(2) are, up to conjugation, given by the following classification:

ADE classification and McKay correspondence

Dynkin diagram/ Dynkin quiver	dihedron, Platonic solid	finite subgroups of SO(3)	finite subgroups of SU(2)	simple Lie group
$A_{n \geq 1}$		cyclic group $\mathbb{Z}_{n+1}$	cyclic group $\mathbb{Z}_{n+1}$	special unitary group $SU(n+1)$
A1		cyclic group of order 2 $\mathbb{Z}_2$	cyclic group of order 2 $\mathbb{Z}_2$	SU(2)
A2		cyclic group of order 3 $\mathbb{Z}_3$	cyclic group of order 3 $\mathbb{Z}_3$	SU(3)
A3 = D3		cyclic group of order 4 $\mathbb{Z}_4$	cyclic group of order 4 $2 D_2 \simeq \mathbb{Z}_4$	SU(4) $\simeq$ Spin(6)
D4	dihedron on bigon	Klein four-group $D_4 \simeq \mathbb{Z}_2 \times \mathbb{Z}_2$	quaternion group $2 D_4 \simeq$ Q8	SO(8), Spin(8)
D5	dihedron on triangle	dihedral group of order 6 $D_6$	binary dihedral group of order 12 $2 D_6$	SO(10), Spin(10)
D6	dihedron on square	dihedral group of order 8 $D_8$	binary dihedral group of order 16 $2 D_{8}$	SO(12), Spin(12)
$D_{n \geq 4}$	dihedron, hosohedron	dihedral group $D_{2(n-2)}$	binary dihedral group $2 D_{2(n-2)}$	special orthogonal group, spin group $SO(2n)$, $Spin(2n)$
$E_6$	tetrahedron	tetrahedral group $T$	binary tetrahedral group $2T$	E6
$E_7$	cube, octahedron	octahedral group $O$	binary octahedral group $2O$	E7
$E_8$	dodecahedron, icosahedron	icosahedral group $I$	binary icosahedral group $2I$	E8

Here under the double cover projection (using the exceptional isomorphism $SU(2) \simeq Spin(3)$)

$$SU(2) \simeq Spin(3) \overset{\pi}{\longrightarrow} SO(3)$$

all the finite subgroups of $SU(2)$ except the odd-order cyclic groups are the preimages of the corresponding finite subgroups of $SO(3)$, in that we have pullback diagrams

$$\array{ \left\langle \exp \left( \pi \mathrm{i} \tfrac{1}{n} \right) \right\rangle & = & \mathbb{Z}/(2n) &\overset{\phantom{AA}}{\hookrightarrow}& Spin(2) &\overset{\phantom{AA}}{\hookrightarrow}& Spin(3) \\ && \big\downarrow &{}^{(pb)}& \big\downarrow &{}^{(pb)}& \big\downarrow^{ \mathrlap{\pi} } \\ \left\langle Ad_{ \exp \left( \pi \mathrm{i} \tfrac{1}{n} \right) } \right\rangle & = & \mathbb{Z}/n &\overset{\phantom{AA}}{\hookrightarrow}& SO(2) &\overset{\phantom{AA}}{\hookrightarrow}& SO(3) }$$

exhibiting the even order cyclic groups as subgroups of Spin(2), including the minimal case of the group of order 2

$$\array{ \left\langle \exp \left( \pi \mathrm{i} \right) = -1 \right\rangle & = & \mathbb{Z}/2 &\overset{\phantom{AA}}{\hookrightarrow}& Spin(2) &\overset{\phantom{AA}}{\hookrightarrow}& Spin(3) \\ && \big\downarrow &{}^{(pb)}& \big\downarrow &{}^{(pb)}& \big\downarrow^{ \mathrlap{\pi} } \\ \left\langle Ad_{ \exp \left( \pi \mathrm{i} \right) } = e \right\rangle & = & 1 &\overset{\phantom{AA}}{\hookrightarrow}& SO(2) &\overset{\phantom{AA}}{\hookrightarrow}& SO(3) }$$

as well as

$$\array{ \left\langle \exp\left( \pi \mathrm{i} \tfrac{1}{n} \right), \, \mathrm{j} \right\rangle &=& 2 D_{2n} &\overset{\phantom{AA}}{\hookrightarrow}& Pin_-(2) &\overset{\phantom{AA}}{\hookrightarrow}& Spin(3) \\ && \big\downarrow &{}^{(pb)}& \big\downarrow &{}^{(pb)}& \big\downarrow^{ \mathrlap{\pi} } \\ \left\langle Ad_{\exp\left( \pi \mathrm{i} \tfrac{1}{n} \right) }, \, Ad_{\mathrm{j}} \right\rangle && D_{2n} &\overset{\phantom{AA}}{\hookrightarrow}& O(2) &\overset{\phantom{AA}}{\hookrightarrow}& SO(3) }$$

exhibiting the binary dihedral groups as sitting inside the Pin(2)-subgroup of Spin(3),

but only commuting diagrams

$$\array{ \left\langle \exp \left( 2 \pi \mathrm{i} \tfrac{1}{{2n+1}} \right) \right\rangle & = & \mathbb{Z}/(2n+1) &&\overset{\phantom{AA}}{\hookrightarrow}&& Spin(3) \\ && \big\downarrow && && \big\downarrow^{ \mathrlap{\pi} } \\ \left\langle Ad_{ \exp \left( 2 \pi \mathrm{i} \tfrac{1}{2n+1} \right) } \right\rangle & = & \mathbb{Z}/(2n+1) &\overset{\phantom{AA}}{\hookrightarrow}& SO(2) &\overset{\phantom{AA}}{\hookrightarrow}& SO(3) }$$

for the odd order cyclic subgroups.

This goes back to (Klein 1884, chapter I). Full proof for $SO(3)$ is spelled out for instance in (Rees 05, theorem 11, De Visscher 11). The proof for the case of $SL(2,\mathbb{C})$ is spelled out in (Miller-Blichfeldt-Dickson 16) reviewed in (Serrano 14, section 2). The proof of the case for $SU(2)$ given the result for $SO(3)$ is spelled out in Keenan 03, theorem 4.

Finite subgroups of $O(4)$, SO(4) and Spin(4)

For classification of the finite subgroups of $O(4)$ see (duVal 65, Conway-Smith 03)

For finite subgroups of Spin(4): MFF 12, appendix B.

In this classification, the symmetry group of the 120-cell and hence that of the 600-cell is the quotient group $(2 I \times 2 I)/\mathbb{Z}_2$ by the cyclic group of order 2 of the direct product group of two copies of the binary icosahedral group (SadocMosseri 89, p. 172, see MFF 12, table 16).

Finite subgroups of $O(5)$

For classification of the finite subgroups of $O(5)$ see Mecchia-Zimmermann 10

Properties

Subgroup lattice

The subgroup lattice of SU(2) under the three exceptional finite subgroups 2T, 2O, 2I (from Theorem ) looks as follows:

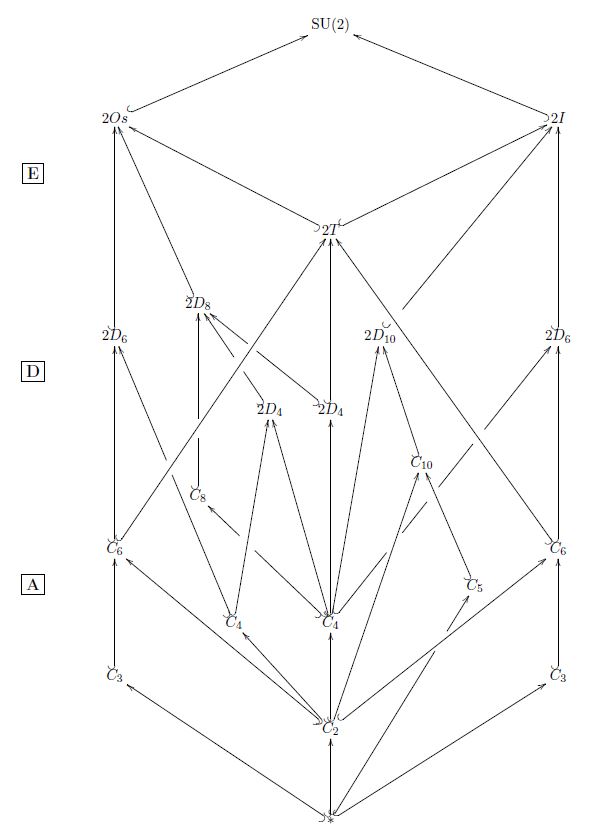
This is obtained from the subgroup lattice as shown on GroupNames for $2I \simeq$ SL(2,5) and $2O \simeq$ CSU(2,3)

See also Goncalves-Guaschi 11, appendix.

Group cohomology

Proposition

(group cohomology of finite subgroups of SU(2))

Let $G_{ADE} \xhookrightarrow{i} SU(2)$ be a finite subgroup of SU(2). Then its group cohomology with integer coefficients is as follows:

(1)$$H^n_{grp}(G_{ADE}, \mathbb{Z}) \;\simeq\; \left\{ \array{ \mathbb{Z} &\vert& n = 0 \\ G_{ADE}^{ab} &\vert& n = 2 \, mod \, 4 \\ \mathbb{Z}/{\vert G_{ADE}\vert} &\vert& n \, \text{positive multiple of} \, 4 \\ 0 &\vert& \text{otherwise} } \right.$$

Here $G_{ADE}^{ab}$ denotes the abelianization of $G_{ADE}$ and $\vert G_{ADE}\vert$ its cardinality, hence $\mathbb{Z}/{\vert G_{ADE}\vert}$ is the cyclic group whose order is the cardinality of $G_{ADE}$.

The group homology with integer coefficients is

(2)$$H_n^{grp}(G_{ADE}, \mathbb{Z}) \;\simeq\; \left\{ \array{ \mathbb{Z} &\vert& n = 0 \\ G^{ab}_{ADE} &\vert& n = 1 \, mod \, 4 \\ \mathbb{Z}/{\vert G_{ADE}\vert} &\vert& n = 3 \,mod\, 4 \\ 0 &\vert& \text{otherwise} } \right.$$

This general statement is summarized in Epa & Ganter 16, p. 12. A detailed proof for the case of cyclic groups is spelled out in BSST 07, Lem. 4.51. The three exceptional cases are worked out in explicit detail in Tomoda & Zvengrowski 08, Section 4. The vanishing of $H^3(G_{ADE},\mathbb{Z}) = H^2(G_{ADE}, \mathbb{C}^\times)$ is also FHHP 01, Cor. 3.1.

Remark

(C-field discrete torsion)

In discussion of 11-dimensional supergravity on spacetimes with ADE-singularities, the special case

$$\underset{ \simeq H^3( \mathbb{C}^4 \sslash G_{ADE}, U(1)) }{ \underbrace{ H^4_{grp}(G_{ADE}, \mathbb{Z}) }} \;\simeq\; \mathbb{Z}/{\vert G_{ADE} \vert }$$

of Prop. , regarded as expressing orbifold cohomology of an ADE singularity, as shown under the brace, witnesses the possible torsion supergravity C-field flux of M5-branes wrapped on torsion homology 3-cycles (“discrete torsion”, see Aharony-Bergman-Jafferis 08, p. 8 and BDHKMMS 01, section 4.6.2).

See also at Platonic 2-group – Relation to String 2-group.

Proposition

For $G_{ADE} \xhookrightarrow{i} Spin(3)$ a finite subgroup of SU(2), the pullback in cohomology along the induced map $B G_{ADE} \xrightarrow{B i} B SU(2)$ of classifying spaces sends

• the generator $c_2 \,\in\,H^4(B SU(2), \mathbb{Z}) \simeq \mathbb{Z}$ (the universal second Chern class)

to

• a generator of $H^4(B G_{ADE}, \mathbb{Z}) \simeq \mathbb{Z}/\left\vert G_{ADE}\right\vert$ (1)

in that the pullback in cohomology is identified with the quotient coprojection from the integers to the cyclic group of order that of $G_{ADE}$:

(3)$$\array{ H^4_{grp}(SU(2), \mathbb{Z}) &=& H^4(B SU(2), \mathbb{Z}) &\simeq& \mathbb{Z} \\ {}^{\mathllap{i^\ast}}\big\downarrow && {}^{\mathllap{B i^\ast}}\big\downarrow && \big\downarrow {}^{\mathrlap{ {quotient} \atop {coprojection} }} \\ H^4_{grp}(G_{ADE}, \mathbb{Z}) &=& H^4(B G_{ADE}, \mathbb{Z}) &\simeq& \mathbb{Z}/\left\vert G_{ADE}\right\vert \mathrlap{\,.} }$$

This is equivalently the statement of Epa & Ganter 16, Prop. 4.1, whose proof is analogous to that of Lemma 3.1 there, where the analogue of (3) is the top left square of the commuting diagram on p. 11.

Related concepts

• regular polytope, regular polyhedron

• ADE singularity

• McKay correspondence

• Platonic 2-group

• wallpaper group

References

Finite subgroups of $SO(3)$ and $Spin(3)$

The classification in Theorem goes back to

• Felix Klein, chapter I of Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünften Grade, 1884, translated as Lectures on the Icosahedron and the Resolution of Equations of Degree Five by George Morrice 1888, online version

Expository review of the argument in Klein 1884:

• Marjorie Senechal, Finding the Finite Groups of Symmetries of the Sphere, The American Mathematical Monthly 97 4 (1990) 329-335 (jstor:2324519)

Textbook accounts:

• G. A. Miller, H. F. Blichfeldt, Leonard E. Dickson, Theory and applications of finite groups, Dover, New York, 1916 (ark:/13960/t0ht2kb4x)

• Klaus Lamotke, Regular Solids and Isolated Singularities, Vieweg 1986 (doi:10.1007/978-3-322-91767-6)

• Mark A. Armstrong, chapter 19 of: Groups and Symmetry, Undergraduate Texts in Mathematics, Springer (1988) [doi:10.1007/978-1-4757-4034-9, pdf]

• Elmer Rees, Notes on Geometry, Springer 2005

see also

• Javier Carrasco Serrano, Finite subgroups of $SL(2,\mathbb{C})$ and $SL(3,\mathbb{C})$, Warwick 2014 (pdf)

Complete proof of the classification of the finite subgroups of $SO(3)$ is also spelled out in

• Maud De Visscher, Groups and Symmetry lecture notes handout: Classification of finite rotation groups (pdf)

Based on the classification of the finite subgroups of $SO(3)$, full proof of that of the finite subgroups of $SU(2)$ is spelled out in

• Adam Keenan, Which finite groups act freely on spheres?, 2003 (pdf)

See also

• Groupprops, Classification of finite subgroups of SO(3,R)

Discussion of the lattice of subgroups of the three exceptional subgroups:

• Daciberg Lima Gonçalves, John Guaschi: The Subgroups of the Binary Polyhedral Groups, Appendix of: The classification of the virtually cyclic subgroups of the sphere braid groups, Briefs in Mathematics, Springer (2013) [arXiv:1110.6628, doi:10.1007/978-3-319-00257-6, pdf]

Discussion of the group cohomology:

• Satoshi Tomoda, Peter Zvengrowski, Remarks on the cohomology of finite fundamental groups of 3-manifolds, Geom. Topol. Monogr. 14 (2008) 519-556 (arXiv:0904.1876)

see also

• Bo Feng, Amihay Hanany, Yang-Hui He, Nikolaos Prezas, Cor. 3.1 in: Discrete Torsion, Non-Abelian Orbifolds and the Schur Multiplier, JHEP 0101:033, 2001 (arXiv:hep-th/0010023)

The universal higher central extension of finite subgroups of $SU(2)$ (“Platonic 2-groups”) are discussed in

• Narthana Epa, Nora Ganter, Platonic and alternating 2-groups, Higher Structures 1(1):122-146, 2017 (arXiv:1605.09192)

Finite subgroups of $O(4)$

• Patrick du Val, Homographies, Quaternions and Rotations, Oxford Mathematical Monographs, Clarendon Press (1964)

  also(?): Journal of the London Mathematical Society, Volume s1-40, Issue 1 (1965) (doi:10.1112/jlms/s1-40.1.569b)

• John Conway, D. A. Smith, On quaternions and octonions: their geometry, arithmetic and symmetry, A K Peters Ltd., Natick, MA, 2003

• Paul de Medeiros, José Figueroa-O'Farrill, appendix B of Half-BPS M2-brane orbifolds, Adv. Theor. Math. Phys. Volume 16, Number 5 (2012), 1349-1408. (arXiv:1007.4761, Euclid)

• J. F. Sadoc, R. Mosseri, Icosahedral order, curved space and quasicrystals, in Jaric, Gratias (eds.) Extended icosahedral structures, 1989 (GoogleBooks)

Finite subgroups of $O(5)$

• Mattia Mecchia, Bruno Zimmermann, On finite groups acting on homology 4-spheres and finite subgroups of $SO(5)$, Topology and its Applications 158.6 (2011): 741-747 (arXiv:1001.3976)