nLab Lie 2-algebra
Context
-Lie theory
∞-Lie theory (higher geometry)
Background
Smooth structure
Higher groupoids
Lie theory
∞-Lie groupoids
∞-Lie algebroids
Formal Lie groupoids
Cohomology
Homotopy
Related topics
Examples
-Lie groupoids
-Lie groups
-Lie algebroids
-Lie algebras
Lie -algebras
Idea
A Lie 2-algebra is to a Lie 2-group as a Lie algebra is to a Lie group. Thus, it is a vertical categorification of a Lie algebra.
Definition
Semistrict case
A (“semistrict”) Lie 2-algebra is an L-∞-algebra with generators concentrated in the lowest two degrees.
This means that it is
-
a pair of vector spaces
-
equipped with linear functions as follows:
a unary bracket encoding a differential
and a binary bracket , whose component on elements in degree 0 is a Lie bracket
and whose component on elements in degree 0 and degree 1 is a weak action
and a trinary bracket
called the Jacobiator;
-
such that
-
and are skew-symmetric in their arguments, as indicated;
-
the differential respects the brackets: for all and we have
hence
-
the Jacobi identity of holds up to the image under of the Jacobiator : for all we have
-
as does the action property:
-
the Jacobiator is coherent:
-
The Jacobiator identity equivalently expresses the commutativity of the following diagram in the given 2-vector space (analogous to the pentagon identity)
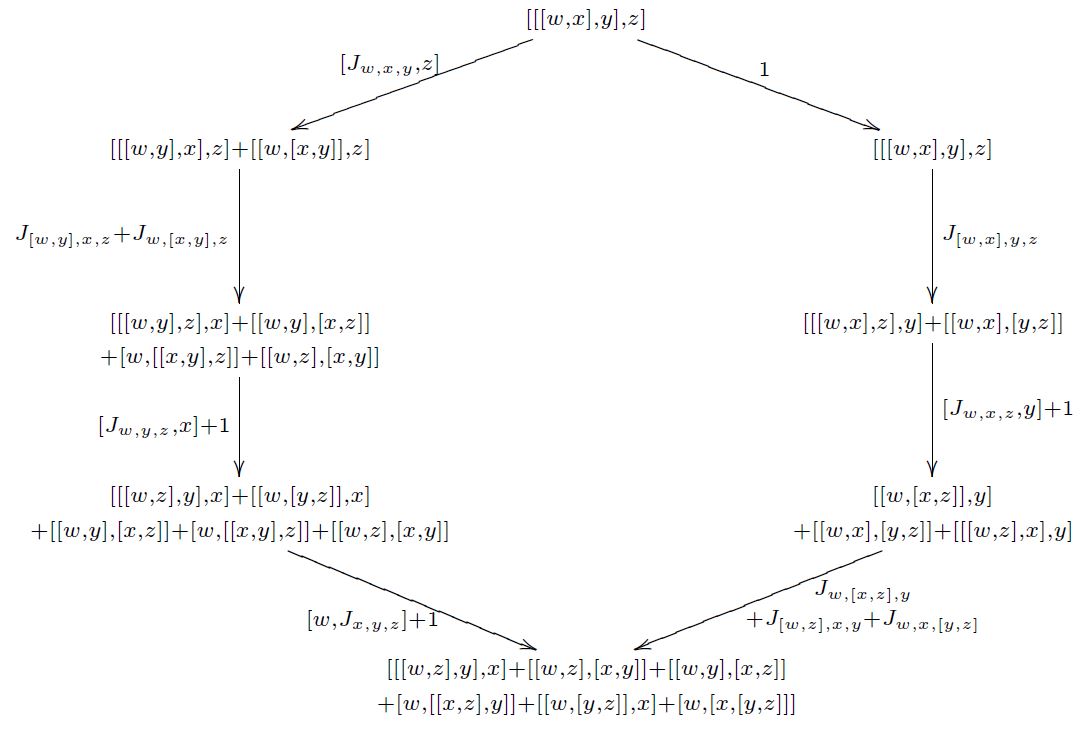
(graphics grabbed from Baez-Crans 04, p. 19)
Strict case
If the trinary bracket in a Lie 2-algebra is trivial, one speaks of a strict Lie 2-algebra. Strict Lie 2-algebras are equivalently differential crossed modules (see there for details).
Examples
Related concepts
-
Lie 2-algebra, Lie 2-group
References
-
John Baez, Alissa Crans, Higher-Dimensional Algebra VI: Lie 2-Algebras Theory and Applications of Categories, Vol. 12, (2004) No. 15, pp 492-528. (TAC:12-15)
-
Daniel Berwick-Evans, Eugene Lerman, Lie 2-algebras of vector fields, arxiv/1609.03944
- Dmitry Roytenberg, On weak Lie 2-algebras, AIP Conference Proceedings 956, 180 (2007) (arXiv:0712.3461, doi:10.1063/1.2820967)
Last revised on July 17, 2022 at 16:07:28. See the history of this page for a list of all contributions to it.