nLab
moduli space of monopoles

Idea

By the Nahm transform, the moduli space of $x^4$-translation invariant self-dual Yang-Mills theory solitons on 4d Euclidean space $\mathbb{R}^{4}$ is equivalently the space of solutions to the Bogomolny equations on 3d Euclidean space, which in turn may be thought of as magnetic monopoles in 3d Euclidean Yang-Mills theory coupled to a charged scalar field (a “Higgs field”). Therefore this moduli space is traditionally referred to simply as the moduli space of magnetic monopoles (e.g. Atiyah-Hitchin 88) or just the moduli space of monopoles.

Definition

The moduli space

(1)$$\mathcal{M}_k \;\coloneqq\; \cdots$$

of $k$ monopoles is … (Atiyah-Hitchin 88, p. 15-16).

Properties

Scattering amplitudes of monopoles

Write

(2)$$Maps_{cplx\,rtnl}^{\ast/}\big( \mathbb{C}P^1, \mathbb{C}P^1 \big)_k \;\subset\; Maps_{cplx\,rtnl}^{\ast/}\big( \mathbb{C}P^1, \mathbb{C}P^1 \big) \;\subset\; Maps^{\ast/}\big( S^2, S^2 \big)$$

for the space of pointed rational functions from the Riemann sphere to itself, of degree $k \in \mathbb{N}$, inside the full Cohomotopy cocycle space. The homotopy type of this mapping space is discussed in Segal 79, see homotopy of rational maps.

To each configuration $c \in \mathcal{M}_k$ of $k \in \mathbb{N}$ magnetic monopoles is associated a scattering amplitude

(3)$$S(c) \in Maps_{cplx\,rtnl}^{\ast/}\big( \mathbb{C}P^1, \mathbb{C}P^1 \big)_k$$

(Atiyah-Hitchin 88 (2.8))

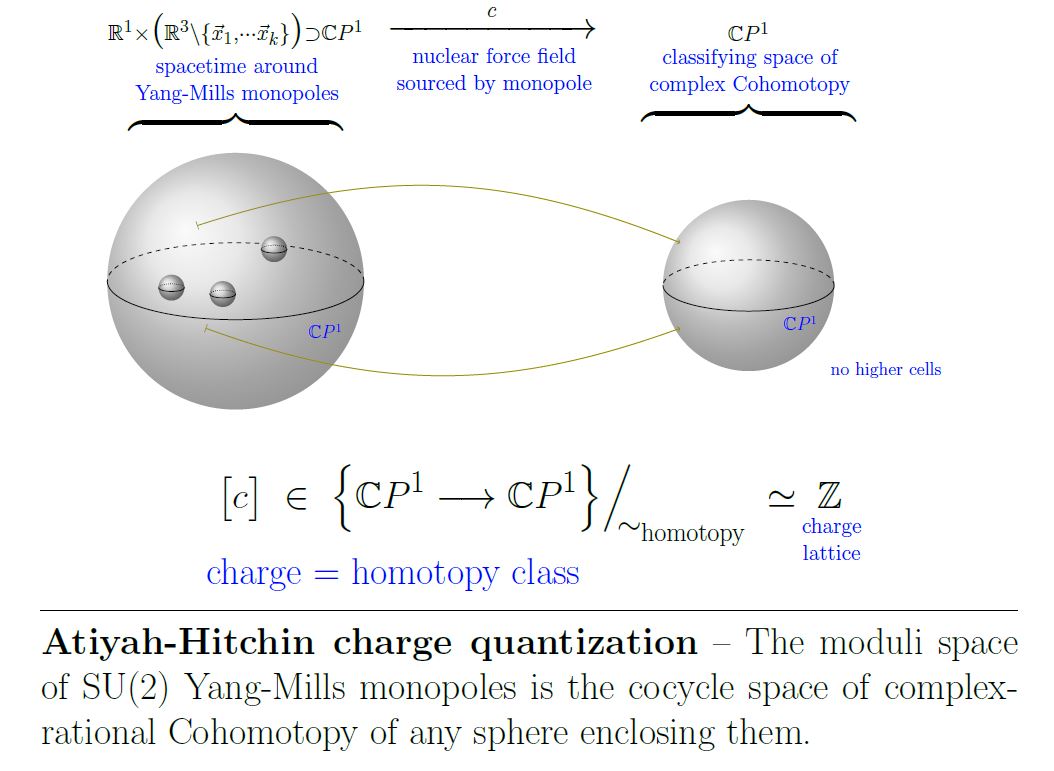
Charge quantization in Cohomotopy

Proposition

(moduli space of k monopoles is space of degree $k$ complex-rational functions from Riemann sphere to itself)

The assignment (3) is a diffeomorphism identifying the moduli space (1) of $k$ magnetic monopoles with the space (2) of complex-rational functions from the Riemann sphere to itself, of degree $k$ (hence the cocycle space of complex-rational 2-Cohomotopy)

$$\mathcal{M}_k \; \underoverset{ \simeq_{diff} }{ S }{ \;\;\longrightarrow\;\; } \; Maps_{cplx\,rtnl}^{\ast/} \big( \mathbb{C}P^1, \mathbb{C}P^1 \big)_k$$

(due to Donaldson 84, see also Atiyah-Hitchin 88, Theorem 2.10).

Proposition

(space of degree $k$ complex-rational functions from Riemann sphere to itself is k-equivalent to Cohomotopy cocycle space in degree $k$)

The inclusion of the complex rational self-maps maps of degree $k$ into the full based space of maps of degree $k$ (hence the $k$-component of the second iterated loop space of the 2-sphere, and hence the plain Cohomotopy cocycle space) induces an isomorphism of homotopy groups in degrees $\leq k$ (in particular a k-equivalence):

$$Maps_{cplx\,rtnl}^{\ast/} \big( \mathbb{C}P^1, \mathbb{C}P^1 \big)_k \; \underset{ \simeq_{\leq k} }{ \;\;\hookrightarrow\;\; } \; Maps^{\ast/}\big( S^2, S^2 \big)_k$$

(Segal 79, Prop. 1.1, see at homotopy of rational maps)

Hence, Prop. and Prop. together say that the moduli space of $k$-monopoles is $k$-equivalent to the Cohomotopy cocycle space $\mathbf{\pi}^2\big( S^2 \big)_k$.

$$\mathcal{M}_k \; \underoverset{ \simeq_{diff} }{ S }{ \;\;\longrightarrow\;\; } \; Maps_{cplx\,rtnl}^{\ast/} \big( \mathbb{C}P^1, \mathbb{C}P^1 \big)_k \; \underset{ \simeq_{\leq k} }{ \;\;\hookrightarrow\;\; } \; Maps^{\ast/}\big( S^2, S^2 \big)_k$$

This is a non-abelian analog of the Dirac charge quantization of the electromagnetic field, with ordinary cohomology replaced by Cohomotopy cohomology theory:

$\,$

Relation to braid groups

Proposition

(moduli space of monopoles is stably weak homotopy equivalent to classifying space of braid group)

For $k \in \mathbb{N}$ there is a stable weak homotopy equivalence between the moduli space of k monopoles (?) and the classifying space of the braid group $Braids_{2k}$ on $2 k$ strands:

$$\Sigma^\infty \mathcal{M}_k \;\simeq\; \Sigma^\infty Braids_{2k}$$

(Cohen-Cohen-Mann-Milgram 91)

Geometric engineering by D$p$-D$(p+2)$-brane intersections

Generally Dp-D(p+2)-brane intersections geometrically engineer Yang-Mills monopoles in the worldvolume of the higher dimensional D$(p+2)$-branes.

Specifically for $p = 6$, i.e. for D6-D8-brane intersections, this fits with the Witten-Sakai-Sugimoto model geometrically engineering quantum chromodynamics, and then gives a geometric engineering of the Yang-Mills monopoles in actual QCD (HLPY 08, p. 16).

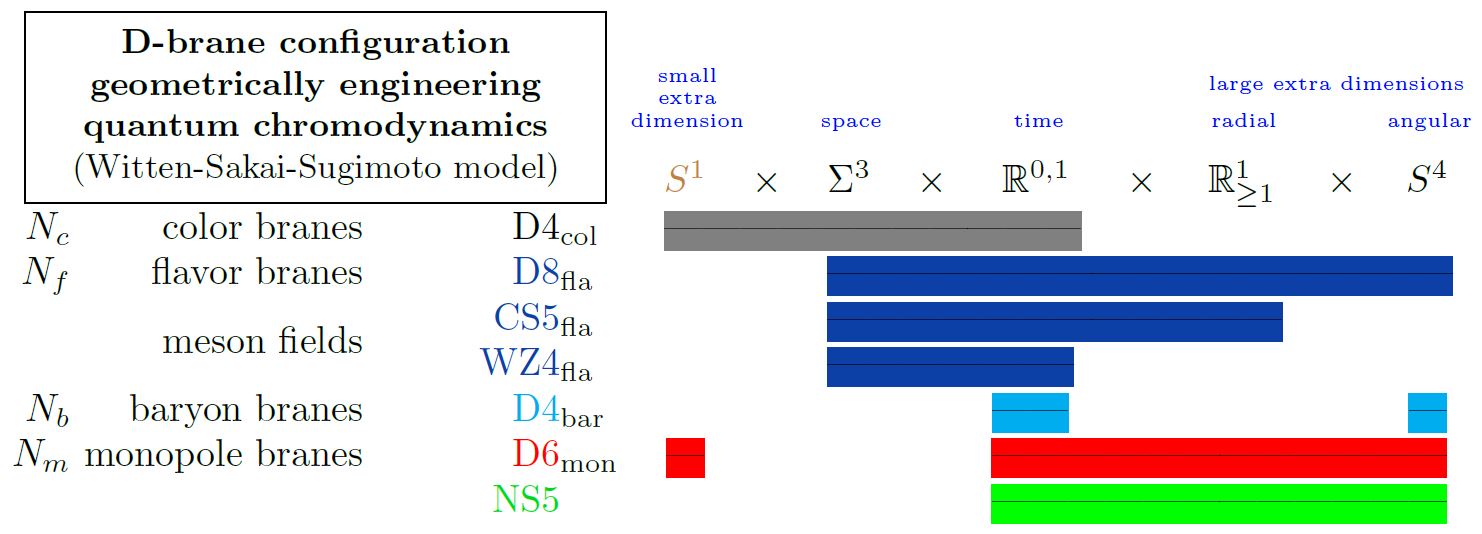
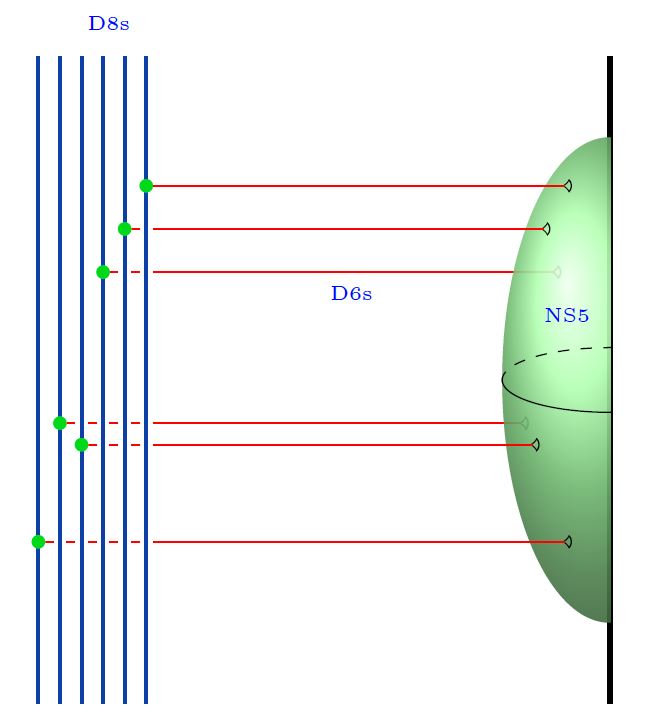
graphics from Sati-Schreiber 19c

Here we are showing

1. the color D4-branes;

2. the flavor D8-branes;

   with

   1. the 5d Chern-Simons theory on their worldvolume

   2. the corresponding 4d WZW model on the boundary

   both exhibiting the meson fields

3. the baryon D4-branes

   (see below at WSS – Baryons)

4. the Yang-Mills monopole D6-branes

   (see at D6-D8-brane bound state)

5. the NS5-branes.

Related concepts

• Nahm transform, Bogomolny equation

moduli spaces

• moduli space of complex structures

• moduli space of conformal structures

• moduli space of curves

• moduli space of Riemannian metrics

• moduli stack of elliptic curves

• moduli space of Calabi-Yau spaces

• moduli stack of tori

• moduli stack of formal groups

• moduli space of connections, moduli space of flat connections

• moduli space of monopoles

• moduli space of framed manifolds

• moduli space of bundles

• moduli space of (higher) line bundles

• quiver variety

References

General

• Michael Atiyah, Nigel Hitchin, J. T. Stuart and M. Tabor, Low-Energy Scattering of Non-Abelian Magnetic Monopoles, Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences Vol. 315, No. 1533, New Developments in the Theory and Application of Solitons (Aug. 13, 1985), pp. 459-469 (jstor:37546)

• Gary Gibbons, Nicholas Manton, Classical and Quantum Dynamics of BPS Monopoles, Nucl. Phys. B274 (1986) 183-224 (spire:18322, doi:10.1016/0550-3213(86)90624-3)

• Michael Atiyah, Nigel Hitchin, The geometry and dynamics of magnetic monopoles, M. B. Porter Lectures. Princeton University Press, Princeton, NJ, 1988 (jstor:j.ctt7zv206)

• Paul Sutcliffe, BPS Monopoles, Int. J. Mod. Phys. A12:4663-4706 (1997) (arXiv:hep-th/9707009, doi:10.1142/S0217751X97002504)

• Yakov Shnir, Part II of: Magnetic Monopoles, Springer 2005 (ISBN:978-3-540-29082-7)

See also:

• Wikipedia, Monopole moduli space

On the ordinary cohomology of the moduli space of YM-monopoles:

• Graeme Segal, Alex Selby, The cohomology of the space of magnetic monopoles, Commun. Math. Phys. 177, 775–787 (1996) (doi:10.1007/BF02099547)

The special case of gauge group SU(3):

• F. A. Bais, Bernd Schroers, Quantisation of Monopoles with Non-abelian Magnetic Charge, Nucl. Phys. B512 (1998) 250-294 (arXiv:hep-th/9708004)

Identification of Yang-Mills monopoles with rational maps

The following lists references concerned with the identification of the (extended) moduli space of Yang-Mills monopoles (in the BPS limit, i.e. for vanishing Higgs potential) with a mapping space of complex rational maps from the complex plane, equivalently holomorphic maps from the Riemann sphere $\mathbb{C}P^1$ (at infinity in $\mathbb{R}^3$) to itself (for gauge group SU(2)) or generally to a complex flag variety such as (see Ionnadou & Sutcliffe 1999a for review) to a coset space by the maximal torus (for maximal symmetry breaking) or to complex projective space $\mathbb{C}P^{n-1}$ (for gauge group SU(n) and minimal symmetry breaking).

The identification was conjectured (following an analogous result for Yang-Mills instantons) in:

• Michael Atiyah, Section 5 of: Instantons in two and four dimensions, Commun. Math. Phys. 93, 437–451 (1984) (doi:10.1007/BF01212288)

Full understanding of the rational map involved as “scattering data” of the monopole is due to:

• Jacques Hurtubise, Monopoles and rational maps: a note on a theorem of Donaldson, Comm. Math. Phys. 100(2): 191-196 (1985) (euclid:cmp/1103943443)

The identification with (pointed) holomorphic functions out of $\mathbb{C}P^1$ was proven…

…for the case of gauge group $SU(2)$ (maps to $\mathbb{C}P^1$ itself) in

• Simon Donaldson, Nahm’s Equations and the Classification of Monopoles, Comm. Math. Phys., Volume 96, Number 3 (1984), 387-407, (euclid:cmp.1103941858)

…for the more general case of classical gauge group with maximal symmetry breaking (maps to the coset space by the maximal torus) in:

• Jacques Hurtubise, The classification of monopoles for the classical groups, Commun. Math. Phys. 120, 613–641 (1989) (doi:10.1007/BF01260389)

• Jacques Hurtubise, Michael K. Murray, On the construction of monopoles for the classical groups, Comm. Math. Phys. 122(1): 35-89 (1989) (euclid:cmp/1104178316)

• Michael Murray, Stratifying monopoles and rational maps, Commun. Math. Phys. 125, 661–674 (1989) (doi:10.1007/BF01228347)

• Jacques Hurtubise, Michael K. Murray, Monopoles and their spectral data, Comm. Math. Phys. 133(3): 487-508 (1990) (euclid:cmp/1104201504)

… for the fully general case of semisimple gauge groups with any symmetry breaking (maps to any flag varieties) in

• Stuart Jarvis, Euclidian Monopoles and Rational Maps, Proceedings of the London Mathematical Society 77 1 (1998) 170-192 (doi:10.1112/S0024611598000434)

• Stuart Jarvis, Construction of Euclidian Monopoles, Proceedings of the London Mathematical Society, 77 1 (1998) (doi:10.1112/S0024611598000446)

and for un-pointed maps in

• Stuart Jarvis, A rational map of Euclidean monopoles via radial scattering, J. Reine angew. Math. 524 (2000) 17-41(doi:10.1515/crll.2000.055)

Further discussion:

• Charles P. Boyer, B. M. Mann, Monopoles, non-linear $\sigma$-models, and two-fold loop spaces, Commun. Math. Phys. 115, 571–594 (1988) (arXiv:10.1007/BF01224128)

• Theodora Ioannidou, Paul Sutcliffe, Monopoles and Harmonic Maps, J. Math. Phys. 40:5440-5455 (1999) (arXiv:hep-th/9903183)

• Theodora Ioannidou, Paul Sutcliffe, Monopoles from Rational Maps, Phys. Lett. B457 (1999) 133-138 (arXiv:hep-th/9905066)

Review:

• Alexander B. Atanasov, Magnetic monopoles and the equations of Bogomolny and Nahm (pdf), chapter 5 in: Magnetic Monopoles, ‘t Hooft Lines, and the Geometric Langlands Correspondence, 2018 (pdf, slides)

On the relevant homotopy of rational maps (see there for more references):

• Graeme Segal, The topology of spaces of rational functions, Acta Math. Volume 143 (1979), 39-72 (euclid:1485890033)

As transversal D$p$/D$(p+2)$-brane intersections

In string theory Yang-Mills monopoles are geometrically engineeted as transversally intersecting Dp-D(p+2)-brane bound states:

For transversal D1-D3-brane bound states:

• Duiliu-Emanuel Diaconescu, D-branes, Monopoles and Nahm Equations, Nucl. Phys. B503 (1997) 220-238 (arxiv:hep-th/9608163)

• Amihay Hanany, Edward Witten, Type IIB Superstrings, BPS Monopoles, And Three-Dimensional Gauge Dynamics, Nucl. Phys. B492:152-190, 1997 (arxiv:hep-th/9611230)

• Jessica K. Barrett, Peter Bowcock, Using D-Strings to Describe Monopole Scattering (arxiv:hep-th/0402163)

• Jessica K. Barrett, Peter Bowcock, Using D-Strings to Describe Monopole Scattering - Numerical Calculations (arxiv:hep-th/0512211)

For transversal D2-D4 brane intersections (with an eye towards AdS/QCD):

• Alexander Gorsky, Valentin Zakharov, Ariel Zhitnitsky, On Classification of QCD defects via holography, Phys. Rev. D79:106003, 2009 (arxiv:0902.1842)

For transversal D3-D5 brane intersections:

• Davide Gaiotto, Edward Witten, Supersymmetric Boundary Conditions in N=4 Super Yang-Mills Theory, J Stat Phys (2009) 135: 789 (arXiv:0804.2902)

For transversal D6-D8-brane intersections (with an eye towards AdS/QCD):

• Deog Ki Hong, Ki-Myeong Lee, Cheonsoo Park, Ho-Ung Yee, Section V of: Holographic Monopole Catalysis of Baryon Decay, JHEP 0808:018, 2008 (https:arXiv:0804.1326)

With emphasis on half NS5-branes in type I' string theory:

• Amihay Hanany, Alberto Zaffaroni, Monopoles in String Theory, JHEP 9912 (1999) 014 (arxiv:hep-th/9911113)

The moduli space of monopoles appears also in the KK-compactification of the M5-brane on a complex surface (AGT-correspondence):

• Benjamin Assel, Sakura Schafer-Nameki, Jin-Mann Wong, M5-branes on $S^2 \times M_4$: Nahm’s Equations and 4d Topological Sigma-models, J. High Energ. Phys. (2016) 2016: 120 (arxiv:1604.03606)

As Coulomb branches of $D=3$ $\mathcal{N}=4$ SYM

Identification of the Coulomb branch of D=3 N=4 super Yang-Mills theory with the moduli space of monopoles in Yang-Mills theory:

• Nathan Seiberg, Edward Witten, Gauge Dynamics And Compactification To Three Dimensions, In: J.M. Drouffe, J.B. Zuber (eds.) The mathematical beauty of physics: A memorial volume for Claude Itzykson Proceedings, Conference, Saclay, France, June 5-7, 1996 (arXiv:hep-th/9607163, spire:420925)

• N. Dorey, V. V. Khoze, M. P. Mattis, David Tong, S. Vandoren, Instantons, Three-Dimensional Gauge Theory, and the Atiyah-Hitchin Manifold, Nucl. Phys. B502 (1997) 59-93 (arXiv:hep-th/9703228)

• David Tong, Three-Dimensional Gauge Theories and ADE Monopoles, Phys. Lett. B448 (1999) 33-36 (arXiv:hep-th/9803148)

• Mathew Bullimore, Tudor Dimofte, Davide Gaiotto, The Coulomb Branch of 3d $\mathcal{N}=4$ Theories, Commun. Math. Phys. (2017) 354: 671 (arXiv:1503.04817)

• Alexander Braverman, Michael Finkelberg, Hiraku Nakajima, Coulomb branches of 3d $\mathcal{N}=4$ quiver gauge theories and slices in the affine Grassmannian (with appendices by Alexander Braverman, Michael Finkelberg, Joel Kamnitzer, Ryosuke Kodera, Hiraku Nakajima, Ben Webster, and Alex Weekes), Advances in Theoretical and Mathematical Physics Volume 23 (2019) Number 1 (arXiv:1604.03625)

Rozansky-Witten invariants

Discussion of Rozansky-Witten invariants of moduli spaces of monopoles:

• Lev Rozansky, Edward Witten, p. 36 of: Hyper-Kähler geometry and invariants of 3-manifolds, Selecta Math., New Ser. 3 (1997), 401–458 (arXiv:hep-th/9612216, doi:10.1007/s000290050016, MR98m:57041)

Relation to braids

Relation to braid groups:

• Fred Cohen, Ralph Cohen, B. M. Mann, R. James Milgram, The topology of rational functions and divisors of surfaces, Acta Math (1991) 166: 163 (doi:10.1007/BF02398886)

• Ralph Cohen, John D. S. Jones, Monopoles, braid groups, and the Dirac operator, Comm. Math. Phys. Volume 158, Number 2 (1993), 241-266 (euclid:cmp/1104254240)

Relation of Dp-D(p+2)-brane bound states (hence Yang-Mills monopoles) to Vassiliev braid invariants via chord diagrams computing radii of fuzzy spheres:

• Sanyaje Ramgoolam, Bill Spence, S. Thomas, Section 3.2 of: Resolving brane collapse with $1/N$ corrections in non-Abelian DBI, Nucl. Phys. B703 (2004) 236-276 (arxiv:hep-th/0405256)

• Simon McNamara, Constantinos Papageorgakis, Sanyaje Ramgoolam, Bill Spence, Appendix A of: Finite $N$ effects on the collapse of fuzzy spheres, JHEP 0605:060, 2006 (arxiv:hep-th/0512145)

• Simon McNamara, Section 4 of: Twistor Inspired Methods in Perturbative FieldTheory and Fuzzy Funnels, 2006 (spire:1351861, pdf, pdf)

• Constantinos Papageorgakis, p. 161-162 of: On matrix D-brane dynamics and fuzzy spheres, 2006 (pdf)