nLab Nahm's equation

Idea

(…)

Properties

Transveral Dp-D(p+2)-brane intersections in fuzzy funnels

The boundary condition in the nonabelian DBI model of coincident Dp-branes describing their transversal intersection/ending with/on D(p+2)-branes is controled by Nahm's equation and thus exhibits the brane intersection-locus equivalently as:

1. a fuzzy funnel noncommutative geometry interpolating between the $\mathrm{D}p$- and the $\mathrm{D}(p+2)$-brane worldvolumes;

2. geometric engineering of Yang-Mills monopoles in the worldvolume-theory of the ambient $D(p+2)$-branes.

(Diaconescu 97, Constable-Myers-Fafjord 99, Hanany-Zaffaroni 99, Gaiotto-Witten 08, Section 2.4, HLPY 08, GZZ 09)

More explicitly, for $y \in (0,\infty ]$ the transversal distance along the stack of $N$ $\mathrm{D}p$-branes away from the $\mathrm{D}(p+2)$-brane, and for

$$X^i \in C^\infty\big( (0,\infty], \mathfrak{u}(N) \big) \phantom{AAA} i \in \{1,2,3\}$$

the three scalar fields on the worldvolume, the boundary condition is:

$$\frac{d}{d y} X^3 + [X^1, X^2] \;=\; 0 \,, \;\;\; \frac{d}{d y} X^1 + [X^2, X^3] \;=\; 0 \,, \;\;\; \frac{d}{d y} X^2 + [X^3, X^1] \;=\; 0$$

as $y \to 0$. These are Nahm's equations, solved by

$$X^i(y) = \frac{1}{y} \rho^i + \text{non-singular}$$

where

$$\rho \;\colon\; \mathfrak{su}(2) \longrightarrow \mathfrak{u}(N)$$

is a Lie algebra homomorphism from su(2) to the unitary Lie algebra, and

$$\rho^i \coloneqq \rho(\sigma^i)$$

is its complex-linear combination of values on the canonical Pauli matrix basis.

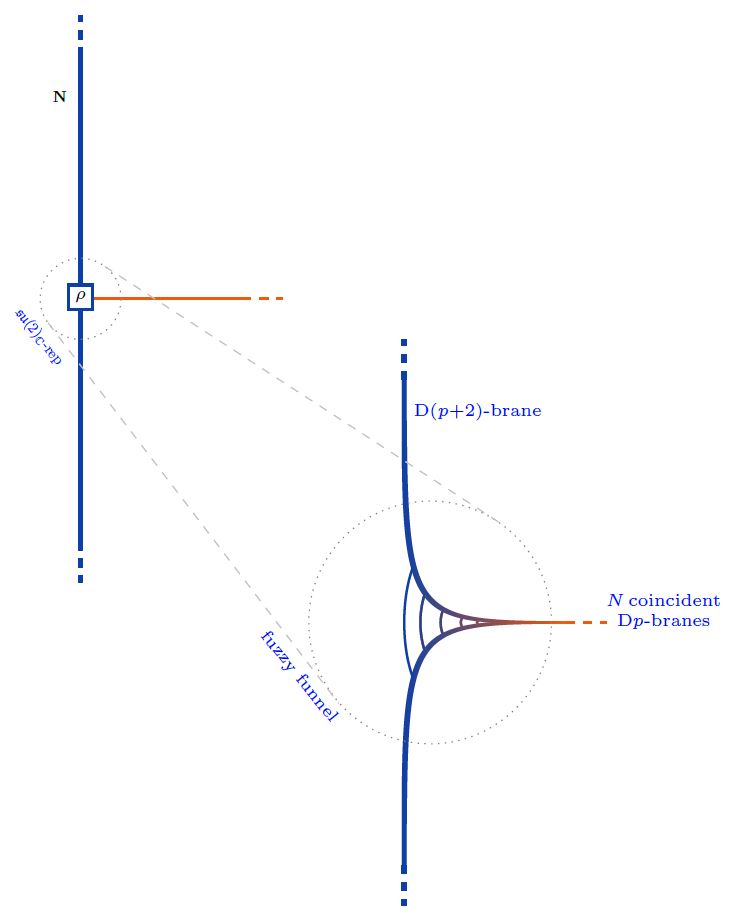
Equivalently. $\rho$ is an $N$-dimensional complex Lie algebra representation of su(2). Any such is reducible as a direct sum of irreducible representations $\mathbf{N}^{(M5)}$, for which there is exactly one, up to isomorphism, in each dimension $N^{(M5)} \in \mathbb{N}$:

(1)$$\rho \;\simeq\; \underset{ i }{\bigoplus} \big( N_i^{(M2)} \cdot \mathbf{N}_i^{(M5)} \big) \,.$$

(Here the notation follows the discussion at M2/M5-brane bound states in the BMN model, which is the M-theory lift of the present situation).

Now each irrep $\mathbf{N}_i^{(M5)}$ may be interpreted as a fuzzy 2-sphere of radius $\propto \sqrt{ \left( N_i^{(M5)}\right)^2 - 1 }$, hence as the section of a fuzzy funnel at given $y = \epsilon$, whence the totality of (1) represents a system of concentric fuzzy 2-spheres/fuzzy funnels.

graphics from Sati-Schreiber 19c

Moreover, since the complexification of su(2) is the complex special linear Lie algebra $\mathfrak{sl}(2,\mathbb{C})$ (here) the solutions to the boundary conditions are also identified with finite-dimensional $\mathfrak{sl}(2,\mathbb{C})$ Lie algebra representations:

(2)$$\rho \;\in\; \mathfrak{sl}(2,\mathbb{C}) Rep \,.$$

This is what many authors state, but it is not yet the full picture:

Also the worldvolume Chan-Paton gauge field component $A$ along $y$ participates in the brane intersection

$$A \in C^\infty\big( (0,\infty], \mathfrak{u}(N) \big)$$

its boundary condition being that

$$[A, X^i] \;=\; 0 \phantom{AAAA} \text{for all}\; i \in \{1,2,3\}$$

as $y \to 0$ (Constable-Myers 99, Section 3.3, Thomas-Ward 06, p. 16, Gaiotto-Witten 08, Section 3.1.1)

Together with (2) this means that the quadruple of fields $(X^1,X^2,X^3,A)$ constitutes a Lie algebra representation of the general linear Lie algebra

$$\mathfrak{gl}(2,\mathbb{C}) \;\simeq\; \underset{ \langle X^1, X^2, X^3 \rangle }{ \underbrace{ \mathfrak{sl}(2,\mathbb{C}) } } \oplus \underset{ \langle A \rangle }{ \underbrace{ \mathbb{C} } }$$

This makes little difference as far as bare Lie algebra representations are concerned, but it does make a crucial difference when these are regarded as metric Lie representations of metric Lie algebras, since $\mathfrak{gl}(2,\mathbb{C})$ admits further invariant metrics…

Related concepts

• Yang-Mills monopole

  • fuzzy funnel

  • D1-D3-brane intersection

  • Dp-D(p+2)-brane intersection

• Yang-Mills instanton

• ADHM construction

• magnetic monopole

• caloron correspondence

• moduli space of monopoles

References

General

The original articles;

• Werner Nahm, The construction of all self-dual multi-monopoles by the ADHM method, In: Craigie et al. (eds.), Monopoles in quantum theory, Singapore, World Scientific 1982 (spire:178340)

• Werner Nahm, Self-dual monopoles and calorons, In: G. Denardo, G. Ghirardi and T. Weber (eds.), Group theoretical methods in physics, Lecture Notes in Physics 201. Berlin, Springer-Verlag 1984 (doi:10.1007/BFb0016145)

• Simon Donaldson, Nahm’s Equations and the Classification of Monopoles, Comm. Math. Phys., Volume 96, Number 3 (1984), 387-407, (euclid:cmp.1103941858)

Further discussion:

• Rafe Mazzeo, Edward Witten, The Nahm Pole Boundary Condition, In: The influence of Solomon Lefschetz in geometry and topology, Contemporary Mathematics 621 (2014): 171 (arXiv:1311.3167, doi:10.1090/conm/621)

Review:

• Marcos Jardim, A survey on Nahm transform, J Geom Phys 52 (2004) 313-327 (arxiv:math/0309305)

• Reinier Storm, The Yang-Mills Moduli Space and The Nahm Transform (dspace:1874/285043)

See also

• Wikipedia, Nahm equations

In terms of Coulomb branch singularities in SYM

In terms of Coulomb branch singularities on super Yang-Mills theories:

• Mathew Bullimore, Tudor Dimofte, Davide Gaiotto, The Coulomb Branch of 3d $\mathcal{N}=4$ Theories, Commun. Math. Phys. (2017) 354: 671 (arXiv:1503.04817)

In term of Dp-D(p+2) brane intersections

On transversal Dp-D(p+2) brane intersections as Yang-Mills monopoles / fuzzy funnel-solutions to Nahm's equation:

For transversal D1-D3 brane intersections:

• Duiliu-Emanuel Diaconescu, D-branes, Monopoles and Nahm Equations, Nucl. Phys. B503 (1997) 220-238 (arxiv:hep-th/9608163)

• Amihay Hanany, Edward Witten, Type IIB Superstrings, BPS Monopoles, And Three-Dimensional Gauge Dynamics, Nucl. Phys. B492:152-190, 1997 (arxiv:hep-th/9611230)

• Jessica K. Barrett, Peter Bowcock, Using D-Strings to Describe Monopole Scattering (arxiv:hep-th/0402163)

• Jessica K. Barrett, Peter Bowcock, Using D-Strings to Describe Monopole Scattering - Numerical Calculations (arxiv:hep-th/0512211)

For transversal D2-D4-brane bound states (with an eye towards AdS/QCD):

• Alexander Gorsky, Valentin Zakharov, Ariel Zhitnitsky, On Classification of QCD defects via holography, Phys. Rev. D79:106003, 2009 (arxiv:0902.1842)

For transversal D3-D5 brane intersections:

• Davide Gaiotto, Edward Witten, Supersymmetric Boundary Conditions in N=4 Super Yang-Mills Theory, J Stat Phys (2009) 135: 789 (arXiv:0804.2902)

For transversal D6-D8 brane intersections (with an eye towards AdS/QCD):

• Deog Ki Hong, Ki-Myeong Lee, Cheonsoo Park, Ho-Ung Yee, Section V of: Holographic Monopole Catalysis of Baryon Decay, JHEP 0808:018, 2008 (https:arXiv:0804.1326)

and as transversal D6-D8-brane bound states on a half NS5-brane in type I' string theory:

• Amihay Hanany, Alberto Zaffaroni, Monopoles in String Theory, JHEP 9912 (1999) 014 (arxiv:hep-th/9911113)

Making explicit the completion of the $\mathfrak{su}(2)_{\mathbb{C}} \simeq \mathfrak{sl}(2,\mathbb{C})$-representation to a $\mathfrak{gl}(2,\mathbb{C})$-representation by adjoining the gauge field component $A_y$ to the scalar fields $\vec X$:

• Gaiotto-Witten 08, Section 3.1.1

• Sergey Cherkis, Instantons on Gravitons, around (21) in: Commun. Math. Phys. 306:449-483, 2011 (arXiv:1007.0044)

Lift to M-theory

The lift of Dp-D(p+2)-brane bound states in string theory to M2-M5-brane bound states/E-strings in M-theory, under duality between M-theory and type IIA string theory+T-duality, via generalization of Nahm's equation (this eventually motivated the BLG-model/ABJM model):

• Anirban Basu, Jeffrey Harvey, The M2-M5 Brane System and a Generalized Nahm’s Equation, Nucl.Phys. B713 (2005) 136-150 (arXiv:hep-th/0412310)

• Jonathan Bagger, Neil Lambert, Sunil Mukhi, Constantinos Papageorgakis, Section 2.2.1 of Multiple Membranes in M-theory, Physics Reports, Volume 527, Issue 1, 1 June 2013, Pages 1-100 (arXiv:1203.3546, doi:10.1016/j.physrep.2013.01.006)