nLab Schur functor

Idea and definition

Classically, a ‘Schur functor’ is a specific sort of functor

$$S \,\colon\, FinDimVect \longrightarrow FinDimVect$$

where FinDimVect is the category of finite dimensional vector spaces over the complex numbers. Namely, it is a functor where $S(X)$ is obtained by taking the $n$th tensor power of the vector space $X$ and then picking out a subspace that transforms in a certain way with respect to the symmetric group $S_n$. In fact, Schur functors can be defined on a large class of categories resembling FinDimVect: for example, categories of representations of a group, or vector bundles, or coherent sheaves. After an elementary introduction to Schur functors, this article will give a conceptual approach based on the fact that these functors are precisely those that can be ‘naturally’ — or more precisely, ‘pseudonaturally’ defined on all symmetric monoidal linear Cauchy complete categories.

The most famous examples of Schur functors are these:

• For each $n \geq 0$, the $n^{th}$ symmetric power $X \mapsto S^n(X)$ is a Schur functor.

• For each $n \geq 0$, the $n^{th}$ alternating power $X \mapsto \Lambda^n(X)$ is a Schur functor.

More generally, complex irreducible representations of $S_n$ correspond to $n$-box Young diagrams, so Schur functors are usually described with the help of these. An $n$-box Young diagram is simply a pictorial way of writing $n$ as a sum of natural numbers listed in decreasing order. For example, this 17-box Young diagram:

describes the partition of $17$ as $5 + 4 + 4 + 2 + 1 + 1$. However, it also can be used to construct an irreducible complex representation of the permutation group $S_{17}$, and thus a Schur functor.

In general, here is the recipe for constructing the Schur functor $S_\lambda$ associated to an $n$-box Young diagram $\lambda$. For now we only say what this functor does to objects (that is, finite-dimensional vector spaces):

• Given an $n$-box Young diagram $\lambda$ and a vector space $X$, we first form the tensor power $X^{\otimes n}$. We think of each factor in this tensor power as corresponding to a specific box of the Young diagram.

• Then we pick out the subspace of $X^{\otimes n}$ consisting of tensors that are unchanged by any permutation that interchanges two boxes in the same row.

• Then we project this subspace onto the space of tensors that change sign under any permutation that interchanges two boxes in the same column. The result is called $S_\lambda(X)$, where $S_\lambda$ is the Schur functor corresponding to $\lambda$.

It is easy to see from this description that:

• The tall skinny Young diagrams with one column and $n$ rows give the Schur functors $\Lambda^n$.

• The short fat Young diagrams with one row and $n$ columns give the Schur functors $S^n$.

We can also think of this relation between Young diagrams and Schur functors in a slightly more abstract way using the group algebra of the symmetric group, $\mathbb{C}[S_n]$. Suppose $\lambda$ is an $n$-box Young diagram. Then we can think of the operation ‘symmetrize with respect to permutations of the boxes in each row’ as an element $p^S_\lambda \in \mathbb{C}[S_n]$. Similarly, we can think of the operation ‘antisymmetrize with respect to permutations of the boxes in each column’ as an element $p^A_\lambda \in \mathbb{C}[S_n]$. By construction, each of these elements is idempotent:

$$(p^A_\lambda)^2 = p^A_\lambda \, , \; \; (p^S_\lambda)^2 = p^S_\lambda$$

Now, it is easy to see that the product of commuting idempotents is idempotent. The elements $p^S_\lambda$ and $p^A_\lambda$ do not commute, but amazingly, their product

$$p_\lambda = p^A_\lambda p^S_\lambda$$

is idempotent up to a scalar multiple!

This element $p_\lambda \in \mathbb{C}[S_n]$ is called the Young symmetrizer corresponding to the $n$-box Young diagram $\lambda$. There is a functor, called a Schur functor:

$$S_\lambda \colon FinDimVect \to FinDimVect$$

defined on any finite-dimensional vector space $X$ as follows:

$$S_\lambda(X) = p_\lambda X^{\otimes n}$$

Here we are using the fact that $S_n$, and thus its group algebra, acts on $X^{\otimes n}$. Thus, $p_\lambda$ acts as an idempotent operator on $X^{\otimes n}$, and $S_\lambda(X)$ as defined above is the range of this operator.

An even deeper approach to Schur functors is based on the relation between Young diagrams and representations of the symmetric groups. The subspace

$$V_\lambda = p_\lambda \mathbb{C}[S_n] \subseteq \mathbb{C}[S_n]$$

has an obvious right action of the algebra $\mathbb{C}[S_n]$, and thus becomes a representation of the group $S_n$. In fact, it is an irreducible representation of $S_n$, and every irreducible representation of $S_n$ is isomorphic to one of this form. Even better, this recipe sets up a one-to-one correspondence between $n$-box Young diagrams and isomorphism classes of irreducible representations of $S_n$.

(Strictly speaking, to think of $p_\lambda$ as an element of $\mathbb{C}[S_n]$, we must choose a way to label the boxes of the Young diagram with numbers $1, \dots, n$. Such an identification is called a Young tableau. For our purposes it will cause no harm to randomly choose a Young tableau for each Young diagram, since different choices give isomorphic representations $V_\lambda$. In other contexts, the difference between various choices of Young tableaux can be extremely important.)

This description of irreducible representations of $S_n$ paves the way towards an important generalization of Schur functors. First, note that

$$X^{\otimes n} \cong \mathbb{C}[S_n] \otimes_{\mathbb{C}[S_n]} X^{\otimes n}$$

It follows that

$$\array{ S_\lambda(X) &=& p_\lambda X^{\otimes n} \\ &\cong& p_\lambda \mathbb{C}[S_n] \otimes_{\mathbb{C}[S_n]} X^{\otimes n} \\ &\cong& V_\lambda \otimes_{\mathbb{C}[S_n]} X^{\otimes n} }$$

These isomorphisms here are natural, so there is no harm in defining the Schur functor $S_\lambda$ by

$$S_\lambda(-) = V_\lambda \otimes_{\mathbb{C}[S_n]} (-)^{\otimes n}$$

This formula defines the Schur functor not only on objects but also on morphisms. Even better, we can use the same formula to define a functor

$$S_R \colon FinDimVect \to FinDimVect$$

for any representation $R$ of $S_n$, as follows:

$$S_R(-) = R \otimes_{\mathbb{C}[S_n]} (-)^{\otimes n} \, .$$

These more general functors are still called ‘Schur functors’.

Even more generally, any finite direct sum of the Schur functors just described may also be called a Schur functor. In other words, if $R = \{R_n\}_{n \ge 0}$ where $R_n$ is a finite-dimensional representation of $S_n$, and only finitely many of these representations are nonzero, then we define the Schur functor

$$S_R(-) = \bigoplus_{n \ge 0} R_n \otimes_{\mathbb{C}[S_n]} (-)^{\otimes n} \, .$$

• For each $n \geq 0$, the $n^{th}$ tensor power $V \mapsto V^{\otimes n}$ is a Schur functor.

• If $F$ and $G$ are Schur functors, the functor $V \mapsto F(V) \oplus G(V)$ is a Schur functor.

• If $F$ and $G$ are Schur functors, the functor $V \mapsto F(V) \otimes G(V)$ is also a Schur functor.

• If $F$ and $G$ are Schur functors, the composite $V \mapsto F(G(V))$ is a Schur functor. This way of constructing Schur functors is known as plethysm.

The category of Schur functors

There is a category $Schur$ with

• Schur functors $S_R \colon FinDimVect \to FinDimVect$ as objects. Here

  $$S_R(-) = \bigoplus_{n \ge 0} R_n \otimes_{\mathbb{C}[S_n]} (-)^{\otimes n} \,$$

  each $R_n$ is a finite-dimensional representation of $S_n$, and only finitely many of these representations are nonzero.

• natural transformations between such functors as morphisms.

In the rest of this article, we would like to give a conceptual explanation of this category.

As a warm-up, let us note that $\Schur$ has has a nice description in terms of groupoid of finite sets and bijections. This groupoid is the core of the category FinSet, so it is denoted $core(FinSet)$. What is the relation between Schur functors and this groupoid. Every Schur functor is a finite direct sum of Schur functors coming from irreducible representations of symmetric groups $S_n$ for various $n$. But what sort of entity is a direct sum of representations of symmetric groups $S_n$ for various $n$? It is nothing but a representation of the permutation groupoid:

$$\mathbb{P} = \bigsqcup_{n \ge 0} S_n \, ,$$

where objects are natural numbers, all morphisms are automorphisms, and the automorphisms of $n$ form the group $S_n$. In other words, it is a functor

$$R : \mathbb{P} \to Vect$$

But conceptually, the importance of $\mathbb{P}$ is that it is a skeleton of the groupoid of finite sets and bijections. So,

$$\mathbb{P} \simeq core(FinSet) \, .$$

As a result, any Schur functor gives a functor

$$R : core(FinSet) \to Vect$$

Following Joyal‘s work on combinatorics, such functors are known as $Vect$-valued species, or $Vect$-valued structure types. The idea here is that just as an ordinary Set-valued species

$$T : core(FinSet) \to Set$$

assigns to any finite set a set of structures of some type, a $Vect$-valued species assigns to any finite set a vector space of structures of some type, Thanks to the ‘free vector space on a set’ functor

$$F: Set \to Vect \, ,$$

we can linearize any ordinary species $T$ and obtain a linear species $F \circ T$. This process is extremely important in the work of Marcelo Aguiar and Swapneel Mahajan:

• Marcelo Aguiar and Swapneel Mahajan, Monoidal Functors, Species and Hopf Algebras, 2010.

However, not all $Vect$-valued species corresond to Schur functors, because we have defined Schur functors to arise from finite direct sums of irreducible representations of permutation groups. So, $Schur$ is equivalent to the category where:

• objects are polynomial species: that is, functors $R: core(Fin\Set) \to FinDimVect$ such that $R(n) = \{0\}$ for all sufficiently large finite sets $n$;

• morphisms are natural transformations.

We call this the category of polynomial species. The reason for the term ‘polynomial’ is that any functor of the form

$$S_R(X) = \bigoplus_{n \ge 0} R_n \otimes_{\mathbb{C}[S_n]} X^{\otimes n}$$

gives rise to a formal power series called its generating function:

$$\sum_{n \ge 0} \frac{dim(R_n) \, x^n}{n!} \, ,$$

and this power series is a polynomial precisely when $R$ is a polynomial species.

The category of representations of any groupoid has many nice features. For example, it is a symmetric monoidal abelian category, by which we mean a symmetric monoidal category that is also abelian, where tensoring with any object is right exact. So, the category of $Vect$-valued species is symmetric monoidal abelian — and it is easy to check that the subcategory of polynomial species inherits this structure. Since $Schur$ is equivalent to the category of polynomial species, it too is symmetric monoidal abelian.

In particular, $Schur$ has two monoidal structures, $\oplus$ and $\otimes$, defined by

$$(F \oplus G)(V) = F(V) \oplus G(V)$$

and

$$(F \otimes G)(V) = F(V) \otimes G(V)$$

Since $\otimes$ distributes over $\oplus$, these make $Schur$ into a rig category.

In the literature on species, the operation $\oplus$ is often called addition, since adding species this way corresponds to adding their generating functions. Aguiar and Mahajan call $\otimes$ the Hadamard product (see section 8.1.2).

But the category of representations of a groupoid has even more nice features when the groupoid itself has a monoidal structure: then the representation category acquires a monoidal structure thanks to Day convolution. The groupoid $\mathbb{P}$ has, in fact, two important monoidal structures, coming from the product $\times$ and disjoint union $+$ of finite sets. Since $\times$ distributes over $+$, these make $\mathbb{P}$ into a rig category. Thanks to Day convolution, these give the category of representations of $\mathbb{P}$ two more monoidal structures, making it into a rig category in another way. The same is true for the subcategory $Schur$.

In the literature on species, the monoidal structure coming from $+$ is often called multiplication, since multiplying species in this way corresponds to multiplying their generating functions. Aguiar and Mahajan call this monoidal structure the Cauchy product. The monoidal structure coming from $\times$ has no commonly used name, but it deserves to be called the Dirichlet product.

Aguiar and Mahajan point out that some of the relationships between the “pointwise” products (addition and Hadamard) and the “Day” products (Cauchy and Dirichlet) can be described in terms of duoidal categories. Specifically, the Hadamard and Cauchy products form duoidal structures in both orders.

On top of all this, the composite of Schur functors is again a Schur functor. This gives $Schur$ a fifth monoidal structure: the plethystic tensor product. Unlike the four previous monoidal structures, this one is not symmetric.

Mathematicians often work with a decategorified version of $Schur$: its Grothendieck group, also known as the ring of symmetric functions. The various structures that $Schur$ possesses endow this ring with corresponding structures. Among other things, it is the free lambda-ring on one generator. As we shall see, this corresponds to the fact that $Schur$ is the free symmetric monoidal Cauchy complete linear category on one object.

Schur functors on more general categories

We have described Schur functors as special functors

$$F \,\colon\, FinDimVect \to FinDimVect$$

But in fact, functors such as the $n^{th}$ alternating power, $n^{th}$ symmetric power, etc. make sense in much wider contexts. For starters, we can replace the complex numbers by any field $k$ of characteristic zero, and everything in our discussion still works. More importantly, Schur functors can be applied to any symmetric monoidal Cauchy complete linear category (“tensor category”). Here by linear category we mean a category enriched over Vect, the category of vector spaces over $k$. Such a category is Cauchy complete when:

• it has biproducts, also known as direct sums, and

• idempotentssplit.

To illustrate the full breadth of this generalization, here are a few examples:

• the category Vect, consisting of vector spaces over any field $k$ of characteristic zero

• the category FinDimVect, consisting of finite-dimensional vector spaces over $k$

• the category of representations of any group on vector spaces (or finite-dimensional vector spaces) over $k$

• the category of super vector spaces, graded vector spaces or chain complexes over $k$

• for $k = \mathbb{R}$ or $\mathbb{C}$, the category of finite-dimensional real or complex vector bundles over any topological space, or smooth vector bundles over any smooth manifold

• the category of algebraic vector bundles over any algebraic variety (or more generally, scheme or algebraic stack) over $k$

• the category of coherent sheaves of vector spaces over any algebraic variety (or scheme or algebraic stack) over $k$

These examples can be hybridized, and thus they multiply indefinitely: for example, we could take coherent sheaves of chain complexes, or vector bundles equipped with a group action, and so on.

In the following subsections, we explain how to define Schur functors on any category of this sort. A somewhat novel feature of our treatment is that we do not require the theory of Young diagrams to define and study Schur functors.

Our strategy is as follows. We fix a symmetric monoidal Cauchy complete linear category, $C$. The group algebra $k[S_n]$ begins life as a monoid in the symmetric monoidal category FinDimVect. However, we shall explain how interpret it as living in $C$ by a “change of base” functor going from FinDimVect to $C$. This will let us use the Young symmetrizers $p_\lambda$ to construct idempotents on $V^{\otimes k}$ for any object $V \in C$. Splitting these idempotents, we obtain the Schur functors $S_\lambda : C \to C$.

Change of base

To achieve the desired change of base, let $Mat$ be the linear category whose objects are integers $m \geq 0$ and whose morphisms $m \to n$ are $m \times n$ matrices with entries in $k$. Because $C$ is Cauchy complete and in particular has finite biproducts (direct sums), there is an evident linear functor

$$Mat \to C$$

which takes $m$ to $I^m$, the direct sum of $m$ copies of the tensor unit $I$. It is the unique linear functor taking $1$ to $I$, up to unique linear isomorphism. In the case $C = FinDimVect$, the linear functor

$$Mat \to FinDimVect,$$

taking $1$ to $k$, is a linear equivalence (exhibiting $Mat$ as a skeleton of $C$). Because of this equivalence, we could equally well say that there is a linear functor

$$i \colon FinDimVect \to C$$

which, up to unique linear isomorphism, is the unique linear functor taking $k$ to $I$. Notice that a symmetric monoidal functor of this form must take the tensor unit $k$ to $I$ (up to coherent isomorphism, as always), and in fact $i$ is symmetric monoidal, because there is a canonical isomorphism

$$I^m \otimes I^n \cong I^{m n},$$

using the fact that $\otimes$ preserves direct sums in each argument, and the fact that there is a canonical isomorphism $I \otimes I \cong I$.

In summary, we have the following proposition.

Proposition

There is exactly one symmetric monoidal linear functor $i \colon FinDimVect \to C$, up to symmetric monoidal linear isomorphism.

The action of Young symmetrizers

Next we explain how given an object $X \in C$, any Young symmetrizer in $k[S_n]$ acts as an idempotent on $X^{\otimes n}$.

For this we only need to know a little bit about the group algebra $k[S_n]$, which we recall here. By Maschke's theorem, for any finite group $G$, the group algebra $k[G]$ decomposes as a direct sum of matrix algebras

$$\bigoplus_{\lambda} hom(V_\lambda, V_\lambda)$$

where $\lambda$ ranges over isomorphism classes of irreducible representations of $G$. The identity elements of these matrix algebras $hom(V_\lambda, V_\lambda)$ thus correspond to certain special elements $p_\lambda \in k[G]$. Clearly these elements are idempotent:

$$p_\lambda^2 = p_\lambda \, .$$

We are particularly interested in the case $G = S_n$. In this case, we call the idempotents $p_\lambda$ are ‘Young symmetrizers’. However, we will not need the formula for these idempotents.

The key step is to apply base change to $k[S_n]$. Here we exploit the fact that

$$k[S_n] = \bigoplus_{\sigma \in S_n} k$$

is a monoid in the monoidal category FinDimVect. Since $i \colon FinDimVect \to C$ is a monoidal functor, it follows that $i$ carries $k[S_n]$ to a monoid object in $C$, which we again call $k[S_n]$ by abuse of notation. As an object of $C$, we have

(1)$$k[S_n] \cong \bigoplus_{\sigma \in S_n} I$$

There is a general concept of what it means for a monoid in a monoidal category to act on an object in that category. In particular, if $X$ is an object of $C$, the monoid $k[S_n]$ acts on the tensor power $X^{\otimes n}$. To see this, note that for each $\sigma \in S_n$, there is a corresponding symmetry isomorphism

$$\sigma : X^{\otimes n} \to X^{\otimes n}$$

Putting these together with the help of (1) we obtain a morphism

$$k[S_n] \otimes X^{\otimes n} \to X^{\otimes n}$$

which is the desired action.

Finally, we would like to describe how each Young symmetrizer $p_\lambda \in k[S_n]$ acts on $X^{\otimes n}$. Quite generally, any element $x \in k[S_n]$ gives a linear map from $k$ to $k[S_n]$, namely the unique map sending $1$ to $x$. Applying the functor $i$ to this, we obtain a morphism which by abuse of language we call

$$x : I \to k[S_n]$$

This then yields an endomorphism

$$\widetilde{x}: X^{\otimes n} \to X^{\otimes n }$$

given as the composite

$$X^{\otimes n} \stackrel{\cong}{\longrightarrow} I \otimes X^{\otimes n} \stackrel{x \otimes 1}{\longrightarrow} k[S_n] \otimes X^{\otimes n} \longrightarrow X^{\otimes n}$$

It is easy to check that for any $x,y \in k[S_n]$,

$$\widetilde{x y} = \widetilde{x} \widetilde{y}$$

Thus for any Young symmetrizer $p_\lambda$, the morphism

$$\widetilde{p}_\lambda : X^{\otimes n} \to X^{\otimes n}$$

is idempotent, because $p_\lambda$ is.

Constructing Schur functors

By construction, the morphisms

$$\widetilde{p}_\lambda : X^{\otimes n} \to X^{\otimes n}$$

are the components of a natural transformation from the functor $X \mapsto X^{\otimes n}$ to itself. Since idempotents split in $C$, we can form the cokernel of $1 - \widetilde{p}_\lambda$, or in other words, the coequalizer of the pair

$$X^{\otimes n} \stackrel{\widetilde{p}_\lambda}{\underset{1}{\rightrightarrows}} X^{\otimes n}$$

Definition

For any Young diagram $\lambda$, the Schur functor $S_\lambda: C \to C$ is defined as follows. Given an object $X$ of $C$, let $S_\lambda(X)$ be the cokernel of $(1 - \widetilde{p}_\lambda) : X^{\otimes n} \to X^{\otimes n}$. Given a morphism $f: X \to Y$ in $C$, let $S_\lambda(f)$ be the unique map $S_\lambda(X) \to S_\lambda(Y)$ such that

$$\array{ X^{\otimes n} & \to & S_\lambda(X) \\ f^{\otimes n} \downarrow \; \; & & \downarrow S_\lambda(f) \\ Y^{\otimes n} & \to & S_\nu(Y) }$$

commutes, where the horizontal arrows are the cokernel maps.

More generally we can define a Schur functor

$$S_R : C \to C$$

for any finite-dimensional representation $R$ of $S_n$, as follows. We can write $R$ as a finite direct sum of irreducible representations:

$$R = \bigoplus_i V_{\lambda_i}$$

and then define

$$S_R(-) = \bigoplus_i S_{\lambda_i}(-) \, .$$

Schur functors are “natural”

Suppose now that we have a symmetric monoidal linear functor $G: C \to D$. We can think of $G$ as a “change of base category”, and Schur functors are “natural” with respect to change of base.

That is to say: if $G$ is a symmetric monoidal linear functor $C \to D$, then by definition $G$ preserves tensor products (at least up to coherent natural isomorphism), and $G$ will automatically preserve both direct sums (by linearity) as well as splittings of idempotents (as all functors do). Therefore, for a Schur functor $S_\lambda(X) = V_\lambda \otimes_{S_n} X^{\otimes n}$, we have natural isomorphisms

$$\array{ S_{\lambda, D} (G X) = V_{\lambda, D} \otimes_{S_n} (G X)^{\otimes n} & \cong & V_{\lambda, D} \otimes_{S_n} G(X^{\otimes n}) \\ & \cong & G(V_{\lambda, C}) \otimes_{S_n} G(X^{\otimes n}) \\ & \cong & G(V_{\lambda, C} \otimes_{S_n} X^{\otimes n}) \\ & \cong & G(S_{\lambda, C}(X)) }$$

where the first isomorphism uses the symmetric monoidal structure of $G$; the second uses the fact that $V_{\lambda, D} \cong G(V_{\lambda, C})$ because there is, up to isomorphism, only one symmetric monoidal linear functor $FinDimVect \to D$; the third uses the symmetric monoidal structure again and preservation of idempotent splittings.

If $R$ is any representation, then by writing $R$ as a direct sum of irreducible representations $V_\lambda$ and using the fact that $G$ preserves direct sums, we have more generally

$$S_{R, D} \circ G \cong G \circ S_{R, C}.$$

In summary, Schur functors $S_R$ transfer “naturally” across change of base functors $G: C \to D$.

Conceptual description of Schur functors

As we have seen, Schur functors $S_R$ are definable under fairly mild hypotheses: working over a field of characteristic zero, they can be defined on any symmetric monoidal linear category $C$ which is Cauchy complete. So, for such $C$ we can define a Schur functor

$$S_R: C \to C$$

and moreover, if $G: C \to D$ is a symmetric monoidal linear functor, the Schur functors on $C$ and $D$ are “naturally” compatible, in the sense that the diagram

$$\array{ C & \stackrel{G}{\to} & D \\ S_{R, C} \downarrow & & \downarrow S_{R, D} \\ C & \underset{G}{\to} & D }$$

commutes up to a canonical isomorphism $\phi_G: S_{R, D} \circ G \cong G \circ S_{R, C}$, and moreover these $\phi_G$ fit together sensibly when we compose symmetric monoidal linear functors.

In this abstract framework, it may be wondered what significant role is played by the representations $R$ of the symmetric group. The natural isomorphisms $\phi_G$ which relate the Schur functors across change of base $G: C \to D$ are pleasant to observe, but surely this is just some piddling general nonsense in the larger story of Schur functors $S_R$, which are after all deeply studied and incredibly rich classical constructions?

Let us put the question another way. We have seen the Schur functors $S_R$ are constructed in a uniform (or “polymorphic”) way across all symmetric monoidal Cauchy complete linear categories $C$, and this construction is natural with respect to symmetric monoidal change of base functors $G: C \to D$. Or rather: not natural in a strict sense, but pseudonatural in the sense that naturality squares commute up to isomorphism $\phi_G$. Now pseudonaturality is a very general phenomenon in 2-category theory. So the question is: among all such pseudonatural transformations $S$, what is special about the Schur functors $S_R$? What extra properties pick out exactly the Schur functors $S_R$ from the class of all pseudonatural transformations $S$?

The perhaps surprising answer is: no extra properties! That is, the Schur functors $S_R$ are precisely those functors that are defined on all symmetric monoidal Cauchy complete linear $C$ and that are pseudonatural with respect to change of base $G: C \to D$!

Let us now make this precise. Schur functors are defined on certain symmetric monoidal linear categories, but they respect neither the symmetric monoidal structure nor the linear structure. So, we have to forget some of the structure of the objects on which Schur functors are defined. This focuses our attention on the ‘forgetful’ 2-functor

$$U: SymMonLinCauch \to Cat$$

where:

Definition

SymMonLinCauch is the 2-category with

• small symmetric monoidal Cauchy complete linear categories as objects,

• symmetric monoidal linear functors as morphisms,

• symmetric monoidal linear natural transformations as 2-morphisms.

As we shall see, Schur functors correspond to pseudonatural transformations from $U$ to itself, and morphisms between Schur functors correspond to modifications between these pseudonatural transformations. For the reader unaccustomed to these 2-categorical concepts, we recall:

Definition

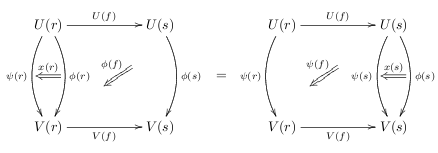
Given two 2-functors $U, V: S \stackrel{\to}{\to} C$ between 2-categories, a pseudonatural transformation $\phi: U \to V$ is a rule that assigns to each 0-cell $s$ of $S$ a 1-cell $\phi(s): U(s) \to V(s)$ of $C$, and to each 1-cell $f: r \to s$ of $S$ an invertible 2-cell $\phi(f)$ of $C$:

$$\array{ U(r) & \stackrel{U(f)}{\to} & U(s) \\ \phi(r) \downarrow & \phi(f) \swArrow & \downarrow \phi(s) \\ V(r) & \underset{V(f)}{\to} & V(s) }$$

such that the following pasting diagram equalities hold:

$$\array{ U(r) & \stackrel{U(f)}{\to} & U(s) & \stackrel{U(g)}{\to} & U(t) & & U(r) & \stackrel{U(g f)}{\to} & U(t) & & \\ \phi(r) \downarrow & \phi(f) \swArrow & \downarrow \phi(s) & \phi(g) \swArrow & \downarrow \phi(t) & = & \phi(r) \downarrow & \phi(g f) \swArrow & \downarrow \phi(t) & & & \\ V(r) & \underset{V(f)}{\to} & V(s) & \underset{V(g)}{\to} & V(t) & & V(r) & \underset{V(g f)}{\to} & V(t) & & & }$$

and

$$\array{ U(r) & \stackrel{U(1_r)}{\to} & U(r) & & \\ \phi(r) \downarrow & \phi(1_r) \swArrow & \downarrow \phi(r) & = & 1_{\phi(r)} \\ V(r) & \underset{V(1_r)}{\to} & V(r) & & }$$

There is also a requirement that the assignation f \mapsto \phi(f) should be natural as f varies along a $2$-cell \alpha: f \Rightarrow g. That is, \phi(g).U\alpha =V\alpha.\phi(f).

Definition

With notation as above, let $\phi, \psi: U \to V$ be two pseudonatural transformations. A modification $x: \phi \to \psi$ is a rule which associates to each 0-cell $s$ of $S$ a 2-cell $x(s): \phi(s) \to \psi(t)$ of $C$, such that the following compatibility condition holds:

We now propose our conceptual definition of Schur functor:

Definition

An (abstract) Schur functor is a pseudonatural transformation $S: U \to U$, where

$$U: SymMonLinCauch \to Cat$$

is the forgetful 2-functor. A morphism of Schur functors is a modification between such pseudonatural transformations.

What this proposed definition makes manifestly obvious is that Schur functors are closed under composition. This provides a satisfying conceptual explanation of plethysm, as we will explore in the next two sections. However, we should first check that this proposed definition gives a category of Schur functors equivalent to the category $Schur$ defined earlier!

Before launching into the proof, it is worth pondering an easier problem where we replace categories by sets, and symmetric monoidal linear Cauchy-complete categories by commutative rings.
So, instead of $Cat$ let us consider $Set$, and instead of $SymMonLinCauch$ let us consider $CommRing$. There is a forgetful functor

$$U : CommRing \to Set \, .$$

What are the natural transformations from this functor to itself? Any polynomial $P \in \mathbb{Z}[x]$ defines such a natural transformation, since for any commutative ring $R$ there is a function $P_R: U(R) \to U(R)$ given by

$$P_R : x \mapsto P(x)$$

and this is clearly natural in $R$. But in fact, the set of natural transformations from this functor turns out to be precisely $\mathbb{Z}[x]$. And the reason is that $\mathbb{Z}[x]$ is the free commutative ring on one generator!

To see this, note that the forgetful functor

$$U : CommRing \to Set$$

has a left adjoint, the ‘free commutative ring’ functor

$$F : Set \to CommRing \, .$$

The free commutative ring on a 1-element set is

$$F(1) \cong \mathbb{Z}[x]$$

and homomorphisms from $F(1)$ to any commutative ring $R$ are in one-to-one correspondence with elements of the underlying set of $R$, since

$$U(R) \cong hom(1, U(R)) \cong hom(F(1), R) \, .$$

So, we say $F(1)$ represents the functor $U$. This makes it easy to show that the set of natural transformations from $U$ to itself is isomorphic to the underlying set of $\mathbb{Z}[x]$, namely $U(F(1))$:

$$[U,U] \cong [hom(F(1), -), hom(F(1), -)] \cong hom(F(1), F(1)) \simeq U(F(1))$$

In the first step here we use the representability $U \cong hom(F(1), -)$; in the second we use the Yoneda lemma, and in the third we use the adjointness between $U$ and $F$.

We shall carry out a categorified version of this argument to prove that $Schur$ is the category of endomorphisms of the 2-functor

$$U: SymMonLinCauch \to Cat$$

The key is that $Schur$ is the free symmetric monoidal linear Cauchy-complete category on one generator.

John Baez: I added explanatory remarks above. Okay?

Representability

To build a bridge from abstract Schur functors as pseudonatural transformations to the more classical descriptions, we start with the following key result. In what follows we use $k \mathbb{P}$ to denote the ‘linearization’ of the permutation groupoid: that is, the linear category formed by replacing the homsets in $\mathbb{P}$ by the free vector spaces on those homsets. We use $\widebar{k \mathbb{P}}$ to denote the Cauchy completion of the linearization of $\mathbb{P}$. As we shall see, $\widebar{k \mathbb{P}}$ is equivalent to the category of Schur functors. But first:

Theorem

The underlying 2-functor

$$U: SymMonLinCauch \to Cat$$

is represented by $\widebar{k \mathbb{P}}$. In other words:

$$U(-) \simeq hom(-, \widebar{k \mathbb{P}})$$

Proof (Sketch)

It is well-known that the permutation category $\mathbb{P}$, whose objects are integers $m \geq 0$ and whose morphisms are precisely automorphisms $m \to m$ given by permutation groups $S_m$, is the representing object for the underlying 2-functor

$$U_0: SymMonCat \to Cat \, .$$

Let $SymMonLin$ denote the 2-category of small symmetric monoidal linear (but not necessarily Cauchy complete) categories, and let $Lin$ denote the 2-category of small linear categories. Let $k(-): Cat \to Lin$ denote linearization, given by change of base

$$k \cdot - : Set \to Vect$$

applied to a $Set$-enriched category $(C_0, hom: C_0 \times C_0 \to Set)$ to yield a linear category $(C_0, C_0 \times C_0 \to Vect)$. $k(-): Cat \to Lin$ is left 2-adjoint to the underlying 2-functor $U_0: Lin \to Cat$. For this, we use the fact that if $V$ is a nice closed category (here $Vect$) – in particular cocomplete – then the lax monoidal functor $\hom(I, -): V \to Set$ has a left adjoint $- \cdot I: Set \to V$ (here linearization) which is strong (symmetric) monoidal. This induces a 2-functor $Cat = Set$-$Cat \to V$-$Cat$ which is strong 2-symmetric monoidal. It therefore sends symmetric pseudomonoids in $Set$-$Cat$ to symmetric pseudomonoids in $V$-$Cat$. In other words, it sends symmetric monoidal categories to symmetric monoidal linear categories. Therefore, the 2-adjunction $k(-) \dashv U_0$ between $Cat$ and $LinCat$ lifts to one between $SymMonCat$ and $SymMonLinCat$:

$$(k(-): SymMonCat \to SymMonLin) \dashv (U_1: SymMonLin \to SymMonCat)$$

Finally, let $LinCauch$ denote the 2-category of small Cauchy complete linear categories. The linear Cauchy completion gives a 2-reflector $\widebar{(-)}: Lin \to LinCat$ which is left 2-adjoint to the 2-embedding $i: LinCauch \to Lin$, and again the 2-adjunction $\widebar{(-)} \dashv i$ lifts to the level of symmetric monoidal structure to give a 2-adjunction

$$(\widebar{(-)}: SymMonLin \to SymMonLinCauch) \dashv (U_2: SymMonLinCauch \to SymMonLin)$$

For this, the key fact is that if $A \otimes B$ denotes the tensor product of two $V$-enriched categories, then there is a canonical enriched functor $\overline{A} \otimes \overline{B} \simeq \overline{A \otimes B}$ making Cauchy completion into a lax 2-monoidal functor on $V$-$Cat$. Even better, it is lax 2-symmetric monoidal. So, it sends symmetric pseudomonoids to symmetric pseudomonoids. In this case, then, it sends symmetric monoidal linear categories to symmetric monoidal linear Cauchy-complete categories.

Putting this all together, the underlying functor $U: SymMonLinCauch \to Cat$ is the evident composite

$$SymMonLinCauch \stackrel{U_2}{\to} SymMonLin \stackrel{U_1}{\to} SymMonCat \stackrel{U_0}{\to} Cat$$

and therefore we have pseudonatural equivalences

$$\array{ SymMonLinCauch(\widebar{k(\mathbb{P})}, -) & \cong & SymMonLin(k(\mathbb{P}), U_2 -) \\ & \cong & SymMonCat(\mathbb{P}, U_1 U_2 -) \\ & \cong & U_0 U_1 U_2 \\ & \cong & U }$$

so that $\widebar{k \mathbb{P}}$ is the representing object.

John Baez: I took remarks from the query box here and used them to improve the proof above. However, it could still use more improvement. Could you polish it up a bit, Todd?

Structure of the representing object

Let us now calculate $\widebar{k \mathbb{P}}$. In general, the linear Cauchy completion of a linear category $C$ consists of the full subcategory of linear presheaves $C^{op} \to Vect$ that are obtained as retracts of finite direct sums of representables $C(-, c): C^{op} \to Vect$. In the case $C = k\mathbb{P}$, these are the functors

$$F \colon \mathbb{P}^{op} \to FinDimVect$$

where $F(n) = 0$ for large enough $n$. For it is clear that this category contains the representables and is closed under finite direct sums and retracts. On the other hand, every polynomial $F$ is a sum of monomials $F(0) \oplus F(1) \oplus \cdots \oplus F(n)$, and by Maschke’s theorem, each $S_j$-module $F(j)$ is the retract of a finite sum of copies of the group algebra $k[S_j]$ which corresponds to the representable $k\mathbb{P}(-, j)$.

So, inspired by Joyal’s work on combinatorial species, we make the following definition:

Definition

A polynomial species is a functor $F: \mathbb{P}^{op} \to FinDimVect$ where $F(n) = 0$ for all sufficiently large $n$. A morphism of polynomial species is a natural transformation between such functors.

As we have mentioned, the category of polynomial species inherits two monoidal structures from $\mathbb{P}$ via Day convolution. Most important is the one coming from the additive monoidal structure on $\mathbb{P}$, which is given on the level of objects by adding natural numbers, and on the morphism level given by group homomorphisms

$$S_m \times S_n \to S_{m+n}$$

which juxtapose permutations. This can be linearized to give algebra maps

$$k[S_m] \otimes k[S_n] \to k[S_{m+n}]$$

which give the monoidal category structure of $k\mathbb{P}$. This monoidal structure uniquely extends via Day convolution to the Cauchy completion $\widebar{k\mathbb{P}}$, which is intermediate between $k\mathbb{P}$ and the category of $Vect$-valued presheaves on $k\mathbb{P}$. The general formula for the Day convolution product applied to presheaves $F, G: \mathbb{P}^{op} \to Vect$ is

$$(F G)(n) = \sum_{j+k = n} (F(j) \otimes G(k)) \otimes_{S_j \times S_k} k[S_n]$$

John Baez: Todd had written $S_n$ where I have put $k[S_n]$ here. Okay?

or, in other notation,

$$(F G)(n) = \sum_{j+k = n} Ind_{S_j \times S_k}^{S_n} F(j) \otimes G(k)$$

and by restriction this formula gives a tensor product on polynomial species. This tensor product is a kind of categorification of the usual definition of product of ordinary polynomials, where given

$$F(x) = \sum_{0 \leq j \leq M} \frac{f_j x^j}{j!} \qquad G(x) = \sum_{0 \leq k \leq N} \frac{g_k x^k}{k!}$$

the $n^{th}$ Taylor coefficient of the product $F(x)G(x)$ is

$$\sum_{j+k = n} \frac{n!}{j! k!} f_j g_k$$

So in summary:

Theorem

$\widebar{k \mathbb{P}}$ is equivalent to the symmetric monoidal category of polynomial species.

Now, having defined Schur functors abstractly as pseudonatural transformations $U \to U$, the representability theorem together with the 2-categorical Yoneda lemma means that the category of Schur functors is equivalent to the category of symmetric monoidal linear functors on $\widebar{k \mathbb{P}}$. Accordingly, we calculate

$$[U, U] \cong SymMonLinCauch(\widebar{k\mathbb{P}}, \widebar{k\mathbb{P}}) \cong U(\widebar{k\mathbb{P}})$$

In other words,

Theorem

The category $Schur$ is equivalent to the category of polynomial species $\mathbb{P}^{op} \to FinDimVect$.

NB: This theorem refers only to the underlying category $U(\overline{k\mathbb{P}})$. In other words, this category certainly has linear tensor category structure as well, but this structure is not respected by Schur functor composition which we consider next.

Composition of Schur functors

Now we consider composition of Schur functors $U \to U$, or equivalently symmetric monoidal linear functors $\widebar{k\mathbb{P}} \to \widebar{k \mathbb{P}}$. Composition endows $[U, U]$ with a monoidal structure, and this monoidal structure transfers across the equivalence of the preceding theorem to a monoidal structure on the underlying category of Schur functors, or equivalently, polynomial species $\mathbb{P}^{op} \to FinDimVect$. We proceed to analyze this monoidal structure.

It may be easier to do this in reverse. Any Schur functor may regarded as a functor

$$1 \stackrel{F}{\to} \overline{k\mathbb{P}} \, .$$

This induces a symmetric monoidal functor, unique up to (unique) symmetric monoidal isomorphism:

$$\mathbb{P} \stackrel{F^\sim}{\to}\overline{k\mathbb{P}}: m \mapsto F^{\otimes m}$$

Here $F^{\otimes m}$ is a Day convolution product of $m$ copies of $F$. Finally, the functor $F^\sim$ is linearized and extended (uniquely) to the linear Cauchy completion, to give a symmetric monoidal linear functor on $\widebar{k \mathbb{P}}$. The efficient tensor product description is

$$- \otimes_{\mathbb{P}} F^\sim: \overline{k\mathbb{P}} \to \overline{k\mathbb{P}}$$

as this manifestly preserves colimits in the blank argument and therefore all colimits needed for the Cauchy completion. (And since the extension to the Cauchy completion is unique, this formula must be correct! The only question is whether this functor is valued in $\overline{k\mathbb{P}}$.)

In the language of species, this construction is called the substitution product, and is denoted $G \circ F$. This is morally correct because it is indeed an appropriate categorification of polynomial composition. However, to avoid overloading the symbol $\circ$ in ways that might be confusing, we will rename it $G \boxtimes F$. Thus,

$$G \boxtimes F = G \otimes_{\mathbb{P}} F^\sim$$

In notation which looks slightly less abstract, this is the Schur object given by the formula

$$(G \boxtimes F)(n) = \sum_{k \geq 0} G(k) \otimes_{S_k} F^{\otimes k}(n)$$

It should be noted that $(G \boxtimes F)(n)$ is indeed $0$ for $n \gt (deg G)(deg F)$, so that $G \boxtimes F$ is indeed a polynomial species. It is just the polynomial special case of the substitution product which is defined on general linear species $F, G: \mathbb{P}^{op} \to Vect$.

Proposition

The product $\boxtimes$ makes the category of polynomial species into a monoidal category. The unit for this product is polynomial species $X$ given by the representable $\mathbb{P}(-, 1): \mathbb{P}^{op} \to FinDimVect$.

Proof (Sketch)

The following proof is adapted from a similar argument due to Max Kelly [ref]: we exhibit an associativity isomorphism $\alpha: (- \boxtimes F) \boxtimes G \to - \boxtimes (F \boxtimes G)$ on the basis of universal properties. The point is that by the universal property of $\overline{k\mathbb{P}}$, the category of functors

$$F: 1 \to \overline{k\mathbb{P}}$$

is equivalent to the category of symmetric monoidal linear functors

$$H: \overline{k\mathbb{P}} \to \overline{k\mathbb{P}}$$

The correspondence in one direction takes $F$ to the symmetric monoidal functor $H = - \boxtimes F$, and in the other direction takes $H$ to $F = H(X)$. By the equivalence, we have a unit isomorphism $X \boxtimes F \cong F$. Also by this equivalence, symmetric monoidal linear transformations between symmetric monoidal linear functors of the form

$$(- \boxtimes F) \boxtimes G \to - \boxtimes (F \boxtimes G)$$

are in natural bijection with morphisms $(X \boxtimes F) \boxtimes G \to X \boxtimes (F \boxtimes G)$, which by the unit isomorphism reduce to morphisms $F \boxtimes G \to F \boxtimes G$. Thus, corresponding to the identity on $F \boxtimes G$ we obtain an associativity map $\alpha: (- \boxtimes F) \boxtimes G \to - \boxtimes (F \boxtimes G)$. By similar arguments that appeal to the universal property of $\overline{k \mathbb{P}}$, we get all the required axioms: the invertibility of $\alpha$, the pentagon, etc.

To summarize: we have equivalences between

• The category of pseudonatural transformations $U \to U$;

• The category of symmetric monoidal linear functors $\overline{k\mathbb{P}} \to \overline{k \mathbb{P}}$;

• The category $Schur = U(\overline{k\mathbb{P}})$.

The equivalence $Schur \to SymMonLinCauch(\overline{k \mathbb{P}}, \overline{k \mathbb{P}})$ takes a polynomial species $F$ to $- \boxtimes F$. Moreover, the associativity isomorphism is precisely a structure

$$(- \boxtimes G) \circ (- \boxtimes F) \to - \boxtimes (F \boxtimes G)$$

of strong monoidal equivalence from $(Schur, \boxtimes)$ to the monoidal category $SymMonLinCauch(\overline{k\mathbb{P}}, \overline{k\mathbb{P}})$ under endofunctor composition. (The hexagonal coherence condition for a monoidal functor follows from the pentagon; one side of the hexagon is an identity since endofunctor composition is a strict monoidal product.)

The tensor product $\boxtimes$ on $Schur$ goes by another name: it is the plethystic tensor product.

Related concepts

• plethory
• Specht module

References

A nice introduction to Schur functors can be found here:

• William Fulton and Joe Harris, Representation Theory: a First Course, Springer, Berlin, 1991.

For a quick online introduction to Young tableaux and representations of the symmetric groups, try:

• Yufei Zhao, Young tableaux and the representations of the symmetric group, MIT. (web)

For more details on these topics, see:

• William Fulton, Young Tableaux, with Applications to Representation Theory and Geometry, Cambridge U. Press, 1997.

• Bruce E. Sagan, The Symmetric Group: Representations, Combinatorial Algorithms, and Symmetric Functions, Springer, Berlin, 2001.

A treatment of the category of Schur functors as the free 2-rig on one generator is in

• John Baez, Joe Moeller, Todd Trimble, Schur functors and categorified plethysm, (arXiv:2106.00190)

Species were invented here:

• André Joyal, Une théorie combinatoire des séries formelles, Adv. Math 42 (1981), 1–82.

• André Joyal: Foncteurs analytiques et espèces des structures, in Combinatoire Énumérative, Lecture Notes in Mathematics 1234, Springer, Berlin, 1986, pp. 126–159.

A standard reference on species is:

• François Bergeron, Gilbert Labelle, Pierre Leroux, Combinatorial Species and Tree-like Structures, Cambridge University Press, Cambridge 1998.

Here is an important new book on combinatorics which emphasizes the use of $Vect$-valued species:

• Marcelo Aguiar and Swapneel Mahajan, Monoidal Functors, Species and Hopf Algebras, to be published by Cambridge U. Press. (web)

Characteristic-free approach to Schur functors and the notion of Schur complexes are developed in

• Kaan Akin, David Alvin Buchsbaum, Jerzy Weyman, Schur functors and Schur complexes, Adv. Math. 44:3 (1982) 207–278
• Marcin Chałupnik, Extensions of Weyl and Schur functors, Homology, Homotopy and Applications 11(2), s. 27-48, 2009.

See also

• Martin Brandenburg, Operations on categories of modules are given by Schur functors (arXiv:1610.02180)

Old Stuff

John Baez: this stuff should go somewhere, perhaps:

The first thing that should be understood from the beginning is that a general Schur functor $F$ is nonlinear: the action on hom-sets

$$hom(V, W) \to hom(F(V), F(W))$$

is not assumed to respect the linear structure. In fact, linear Schur functors are rather uninteresting: because every finite-dimensional space is a finite direct sum of copies of the $1$-dimensional space $\mathbb{C}$, and because linear functors preserve finite direct sums (that is, biproducts, it turns out that every linear Schur functor $F$ is representable as $hom(X, -)$ where $X = F(\mathbb{C})$. So, the category of linear Schur functors is equivalent to $FinDimVect$.

John Baez: This stuff should get worked into the discussion near the end of how Schur functors are like polynomials…

Modules over a bimonoid

Next we exploit the fact that, just like any group algebra, $k[S_n]$ is a bialgebra — or in fancier language, a bimonoid in the symmetric monoidal category FinDimVect${}_k$. Since $i \colon FinDimVect_k \to C$ is a symmetric monoidal functor, this means that $i$ carries $k[S_n]$ to a bimonoid in $C$. As noted above, we call this bimonoid by the same name, $k[S_n]$.

The category of modules over a bimonoid is a monoidal category. More explicitly, in the case of the bimonoid $k[S_n]$ in $C$ with comultiplication

$$\delta: k[S_n] \to k[S_n] \otimes k[S_n] \,,$$

the tensor product $V \otimes W$ of two $k[S_n]$-modules in $C$ carries a module structure where the action is defined by

$$k[S_n] \otimes V \otimes W \stackrel{\delta \otimes 1_{V \otimes W}}{\to} k[S_n] \otimes k[S_n] \otimes V \otimes W \stackrel{1 \otimes \sigma \otimes 1}{\to} k[S_n] \otimes V \otimes k[S_n] \otimes W \stackrel{\alpha_V \otimes \alpha_W}{\to} V \otimes W$$

where $\sigma$ is a symmetry isomorphism and $\alpha_V$, $\alpha_W$ are the actions on $V$ and $W$.

Now we consider a particular case of tensor product representations. If $X$ is an object of $C$, the symmetric group $S_n$ has a representation on $X^{\otimes n}$. (Indeed, for each $\sigma \in S_n$, there is a corresponding symmetry isomorphism $X^{\otimes n} \to X^{\otimes n}$. From this one may construct an action

$$k[S_n] \otimes X^{\otimes n} \cong \bigoplus_{\sigma \in S_n} I \otimes X^{\otimes n} \to X^{\otimes n}$$

which is the required representation.) So, if $V_\nu$ is a Young tableau representation of $k[S_n]$ in $C$, we obtain a tensor product representation

$$V_\nu \otimes X^{\otimes n}$$

of $k[S_n]$ in $C$.

Consider next the averaging operator $e = \frac1{n!} \sum_{\sigma \in S_n} \sigma$:

$$e: V_\nu \otimes X^{\otimes n} \to V_\nu \otimes X^{\otimes n}$$

This operator makes sense since $k$ has characteristic zero, and crucially, this operator is idempotent (because $e = \sigma e$ for all $\sigma \in S_n$). Because we assume idempotents split in $C$, we have a (split) coequalizer

$$V_\nu \otimes X^{\otimes n} \stackrel{\overset{e}{\to}}{\underset{1}{\to}} V_\nu \otimes X^{\otimes n} \to V_\nu \otimes_{S_n} X^{\otimes n}$$

This coequalizer is indeed the object of $S_n$-coinvariants of $V_\nu \otimes X^{\otimes n}$, i.e., the joint coequalizer of the diagram consisting of all arrows

$$V_\nu \otimes X^{\otimes n} \stackrel{\sigma \cdot-}{\to} V_\nu \otimes X^{\otimes n}$$

ranging over $\sigma \in S_n$ (it is the joint coequalizer because $e = \sigma e$ for all $\sigma$).

We may now define the Schur functor $S_\nu$ on $C$ attached to a Young tableau $\nu$.