nLab asymptotic safety
Context
Quantum field theory
Gravity
Formalism
Definition
Spacetime configurations
Properties
Spacetimes
| black hole spacetimes | vanishing angular momentum | positive angular momentum |
|---|---|---|
| vanishing charge | Schwarzschild spacetime | Kerr spacetime |
| positive charge | Reissner-Nordstrom spacetime | Kerr-Newman spacetime |
Quantum theory
Contents
Idea
In the context of quantum field theory (QFT) the term asymptotic safety (Weinberg 79) refers to the situation where a QFT may not be renormalizable (is not defined on all scales by the choice of a finite number of coupling constants), but has the property that its renormalization group flow has a non-trivial non-perturbative fixed point such that the subspace of the space of coupling constants whose RG-flow converges to this fixed point is finite dimensional.
One defines the “UV-critical hypersurface” as the set of all those points in the infinite-dimensional theory space which are “pulled” into the fixed point by the inverse RG flow: trajectories lying in this surface approach the fixed point for increasing momentum scales. General arguments and known examples suggest that the UV-critical hypersurface has a finite dimensionality. This dimensionality equals the number of (infrared-) relevant couplings, i.e. couplings which get attracted to the fixed point in the UV. The important point is that once the value of these (few) couplings are known at some scale all other (irrelevant) couplings are fixed by requiring an asymptotically safe theory, that is a trajectory which lies entirely in the UV-critical hypersurface. By this means we achieve that, first, the couplings are determined by a finite number of measurements rendering the theory predictive, and, second, the UV behavior is unproblematic without any unphysical divergences. (Nink-Reuter 12, p. 2)
A key example of a non-renormalizable QFT is Einstein gravity, and there is speculation that it might be asymptotically safe, and that this might be the solution to the construction of quantum gravity (Reuter 96).
Issues
Issues that the program of asymptotic safety of gravity is facing include the following:
Theoretical issues
-
All existing computations that see hints for a UV-fixed point do so by first applying a drastic truncation to the space of couplings, and then checking only whether there is a UV-fixed point for the RG-flow in the remaining small subspace. It seems unclear to which extent these approximate considerations may be extrapolated.
-
Most existing computations consider only pure Einstein gravity without matter coupling. It seems unclear to which extent these results may be extrapolated to the situation where matter is taken account of (but see Biemans-Platania-Saueressig 17).
-
Donoghue 19 claims technical problems with the handling of renormalization group flow in Newton’s constant as currently practiced in the asymptotic safety program:
-
The “running” comes from power-divergent corrections that vanish in dimensional regularization.
-
Computing different Minkowski spacetime processes gives different power-divergent corrections: there is no generic common .
-
There is no generic energy : some processes depend on , others on and (unlike in the usual log running) this makes a difference.
-
-
If one assumes (as is widely, but no generally believed) that Bekenstein-Hawking entropy seen in classical gravity is to correspond to a microscopic entropy of its quantum degrees of freedom, then the scaling of this entropy with area as opposed to volume contradicts the assumption that quantum gravity is a local field theory at small scales and higher energies (Shomer 07, section IV) and hence then it contradicts the asymptotic safety of gravity.
Similarly, if one trusts the AdS/CFT correspondence then gravity is fundamentally not a local field theory, only its boundary CFT is, in contradiction with asymptotic safety of gravity (Shomer 07, section IV). But see FR22.
Experimental issues
The near criticality of the Higgs field vacuum (see there at Higgs mass and vacuum (in-)stability) implies that the coefficient of the quartic part of the Higgs potential is close to zero after renormalization group flow (“RGE”) to around the Planck scale of about GeV (e.g. BDGGSSS 13, p. 17-18):
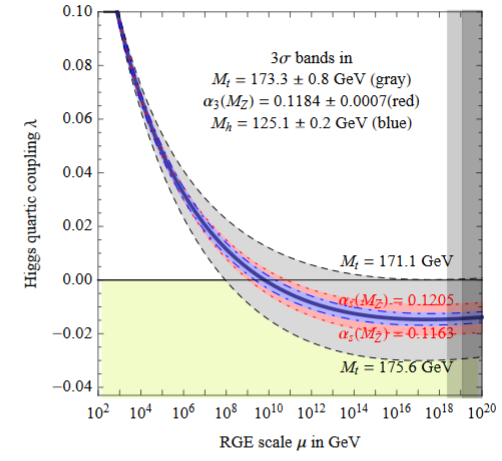
In fact also the beta function of the quartic coupling (i.e. its logarithmic derivative with respect to scale) is close to zero around the Planck scale of about GeV (BDGGSSS 13, p. 18):
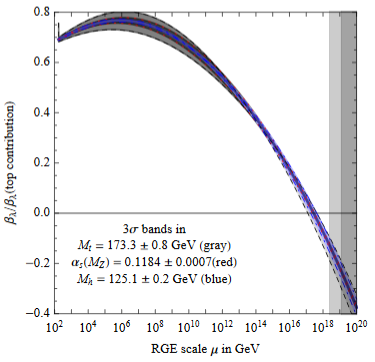
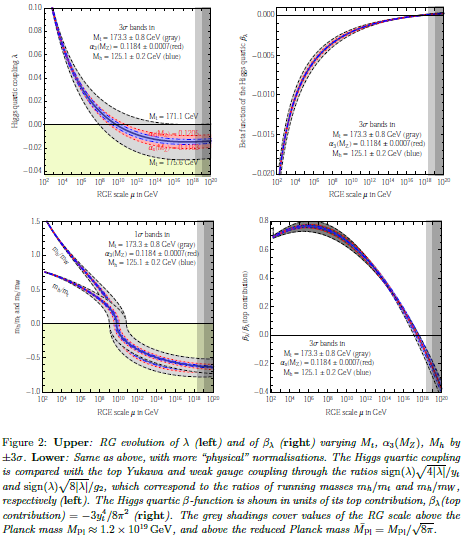
Earlier it has been suggested that this reflects the principle of asymptotic safety (Shaposhnikov-Wetterich 09). But this would mean that not only and its RGE-derivative vanish around the Planck scale, but that in fact all higher derivatives do, too (see e.g Niedermaier 06, equation (1.5)) hence that asymptotes to zero. But this does not seem to be the case; in (BDGGSSS 13, p. 17-18) it says:
As shown in fig. 2 (upper right), the corresponding Higgs quartic beta-function vanishes at a scale of about - GeV. In order to quantify the degree of cancellation in the β-function, we plot in fig. 2 (lower right) in units of its pure top quark contribution. The vanishing of looks more like an accidental cancellation between various large contributions, rather than an asymptotic approach to zero.
References
The idea of asymptotic safety as such and as a cure for quantum gravity is due to
- Steven Weinberg, Ultraviolet divergences in quantum theories of gravitation, in “General Relativity: An Einstein centenary survey”, ed. S. W. Hawking and W. Israel. Cambridge University Press. pp. 790–831 (1979) (spire)
It gained new popularity with this result:
- Martin Reuter, Nonperturbative Evolution Equation for Quantum Gravity, Phys.Rev. D57 (1998) 971-985 (arXiv:hep-th/9605030)
An attempt to conceptually explain why gravity might have a UV-fixed point is in this article:
- Andreas Nink, Martin Reuter, On quantum gravity, Asymptotic Safety, and paramagnetic dominance, Int. J. Mod. Phys. D22 (2013) 1330008 (arXiv:1212.4325)
Observation of a special role of spacetime dimension 2:
- O. Lauscher, Martin Reuter, Asymptotic Safety in Quantum Einstein Gravity: nonperturbative renormalizability and fractal spacetime structure, In: Fauser B., Tolksdorf J., Zeidler E. (eds.) )Quantum Gravity_ Birkhäuser Basel 2006 (arXiv:hep-th/0511260, doi:10.1007/978-3-7643-7978-0_15)
and speculation of this being related to the Connes-Lott model (see here):
- Alain Connes, p. 8 of Noncommutative Geometry and the standard model with neutrino mixing, JHEP0611:081,2006 (arXiv:hep-th/0608226)
Review:
-
Max Niedermaier, The Asymptotic Safety Scenario in Quantum Gravity – An Introduction, Class.Quant.Grav.24:R171-230,2007 (arXiv:gr-qc/0610018)
-
Max Niedermaier, Martin Reuter, The Asymptotic Safety Scenario in Quantum Gravity, Living Reviews in Relativity December 2006, 9:5 doi:10.12942/lrr-2006-5
-
Riccardo Martini, Gian Paolo Vacca, Omar Zanusso, Perturbative approaches to non-perturbative quantum gravity, in: Handbook of Quantum Gravity, Springer (2023) [arXiv:2210.13910]
-
Astrid Eichhorn, Marc Schiffer, Asymptotic safety of gravity with matter, in: Handbook of Quantum Gravity, Springer (2023) [arXiv:2212.07456]
-
Alexander Bednyakov, Alfiia Mukhaeva, Perturbative Asymptotic Safety and Its Phenomenological Applications [arXiv:2309.08258]
-
Jan M. Pawlowski, Manuel Reichert, Quantum Gravity from dynamical metric fluctuations in Handbook of Quantum Gravity [arXiv:2309.10785]
Critical review:
-
Assaf Shomer, A pedagogical explanation for the non-renormalizability of gravity (arXiv:0709.3555)
-
John Donoghue, A Critique of the Asymptotic Safety Program, Frontiers in Physics 8, 56 (2020) (arXiv:1911.02967, doi:10.3389/fphy.2020.00056)
See also:
-
Roberto Percacci, Asymptotic Safety FAQs (web)
-
John Donoghue vs. Roberto Percacci, Debate on Asymptotically Safe Quantum Gravity, Perimeter Institute, April 2021 (video, slides)
-
Jorn Biemans, Alessia Platania, Frank Saueressig, Renormalization group fixed points of foliated gravity-matter systems (arXiv:1702.06539)
The suggestion that asymptotic safety explains the observed mass of the Higgs particle is attributed to
- Mikhail Shaposhnikov, Christof Wetterich, Asymptotic safety of gravity and the Higgs boson mass, Phys. Lett. B 683 (2010) 196 [arXiv:0912.0208]
but see p. 17 of
- Dario Buttazzo, Giuseppe Degrassi, Pier Paolo Giardino, Gian Giudice, Filippo Sala, Alberto Salvio, Alessandro Strumia, section 7 of Investigating the near-criticality of the Higgs boson (arXiv:1307.3536)
and for more see at Higgs field – Asymptotic safety?
Application to scattering amplitudes:
- Jan H. Kwapisz, Krzysztof A. Meissner, Asymptotic safety and quantum gravity amplitudes (arXiv:2005.03559)
Unitarity, causality and stability in Asymptotic Safety:
-
Alessia Platania, Christof Wetterich, Non-perturbative unitarity and fictitious ghosts in quantum gravity (arXiv:2009.06637)
-
Alessia Platania Causality, unitarity and stability in quantum gravity: a non-perturbative perspective (arXiv:2206.04072)
-
Benjamin Knorr, Alessia Platania Unearthing the intersections: positivity bounds, weak gravity conjecture, and asymptotic safety landscapes from photon-graviton flows (2405.08860)
Review on early-universe cosmology in the context of asymptotic safety:
- Alessia Platania, From renormalization group flows to cosmology, Front.in Phys. 8 (2020) 188 [arXiv:2003.13656]
Review on black holes in the context of asymptotic safety:
- Alessia Platania, Black Holes in Asymptotically Safe Gravity, in Handbook of Quantum Gravity, Springer (2023) [arXiv:2302.04272]
See also:
- Edoardo D’Angelo, Asymptotic Safety in Lorentzian quantum gravity [arXiv:2310.20603]
Relation to String Theory:
-
Senarath de Alwis, et al. Asymptotic safety, string theory and the weak gravity conjecture (arXiv:1907.07894)
-
Ivano Basile, Alessia Platania, Cosmological α′-corrections from the functional renormalization group (arXiv:2101.02226)
-
Ivano Basile, Alessia Platania, String tension between de Sitter vacua and curvature corrections (arXiv:2103.06276)
-
Ivano Basile, Alessia Platania, Asymptotic Safety: Swampland or Wonderland? (arXiv:2107.06897)
-
Fei Gao, Masatoshi Yamada, Determining holographic wave functions from Wilsonian renormalization group (arXiv:2202.13699)
-
Renata Ferrero, Martin Reuter, On the possibility of a novel (A)dS/CFT relationship emerging in Asymptotic Safety [arXiv:2205.12030]
-
Benjamin Knorr, Alessia Platania Unearthing the intersections: positivity bounds, weak gravity conjecture, and asymptotic safety landscapes from photon-graviton flows (2405.08860)
-
Ivano Basile, Benjamin Knorr, Alessia Platania, Marc Schiffer Asymptotic safety, quantum gravity, and the swampland: a conceptual assessment (2502.12290)
Last revised on March 27, 2025 at 14:29:36. See the history of this page for a list of all contributions to it.