nLab Higgs field
Context
Fields and quanta
fields and particles in particle physics
and in the standard model of particle physics:
matter field fermions (spinors, Dirac fields)
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
(also: antiparticles)
hadrons (bound states of the above quarks)
minimally extended supersymmetric standard model
bosinos:
dark matter candidates
Exotica
Contents
Idea
The Higgs field or Higgs boson is a scalar physical field/fundamental particle in a gauge theory such as the standard model of particle physics supposedly responsible for the spontaneously broken symmetry of the electroweak field (electroweak symmetry breaking) and for giving elementary particles their masses by the Higgs mechanism.
Properties
Mass and vacuum (in-)stability
The rest mass of the Higgs particle observed at the LHC experiment is about GeV (ATLAS Collaboration 12, CMS Collaboration 12, ATLAS Collaboration 15, see Gibbs 11a, HLL 11 for early discussion).
This is determined by a local minimum of the Higgs potential (see Kusenko 15 for exposition):
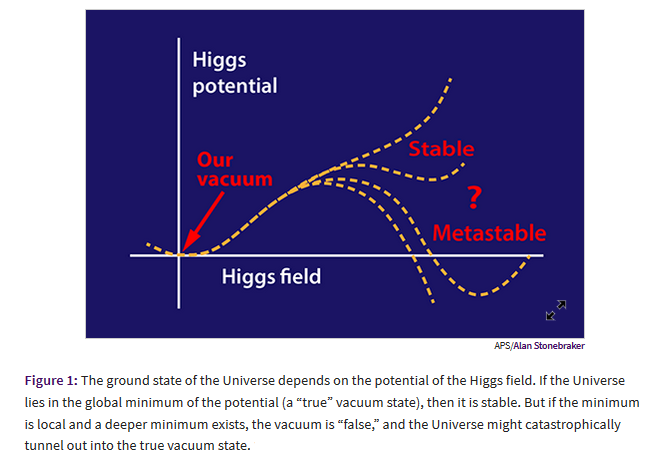
Curiously, the Higgs potential is such that the Higgs field at this mass is at least close to being at the border between vacuum stability and false vacuum. This was highlighted before the actual measurement (EEGHR 09, Gibbs 11b):
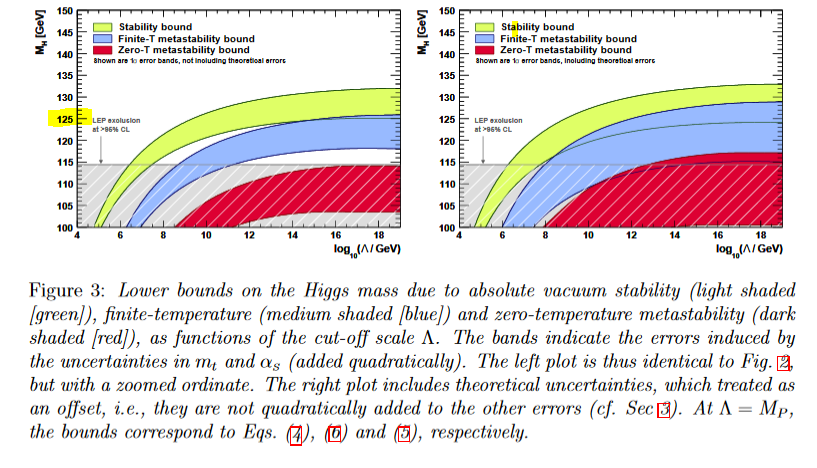
Then it was amplified again after the detection of the Higgs particle at the LHC (DVEEGI 12):
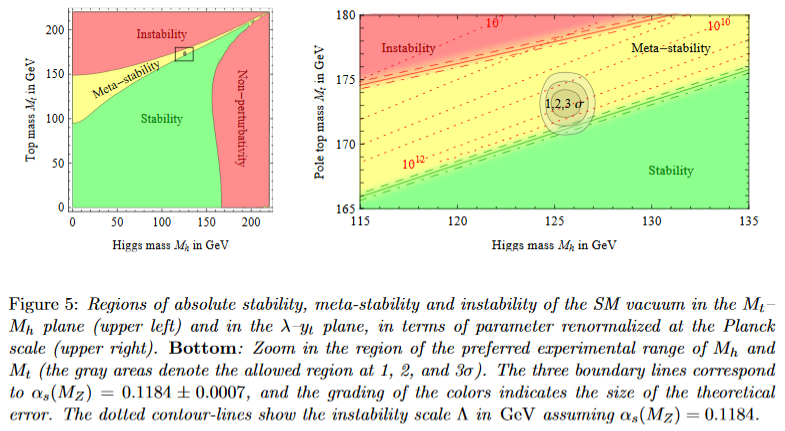
More detailed computation at 2-loop confirmed this result, showing that the observed Higgs vacuum is indeed very close to the boundary between the stable and the meta-stable region (BKPV 15):
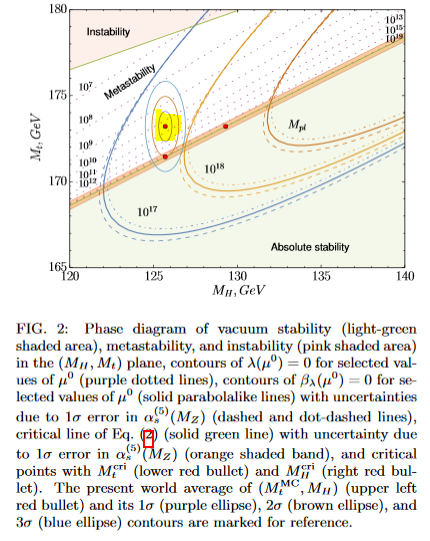
See also AFS 18:
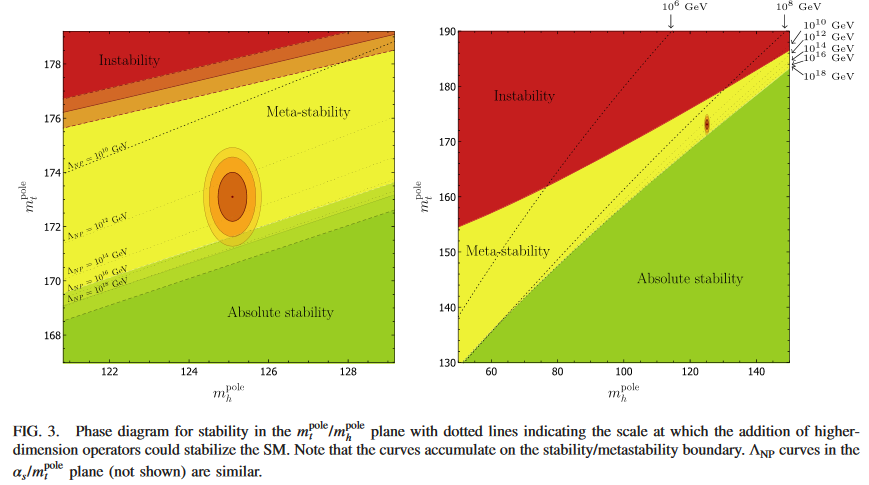
In summary (Kusenko 15):
The conclusion is that the best theoretical fit to measured parameters, including the Higgs and top-quark masses, points to a metastable Universe. However, their analysis also concludes that values of parameters are closer to a region of absolute stability than suggested by previous studies: it is possible for the Universe to be fully stable (and for the standard model to work all the way up to the Planck scale), if the true values of measured parameters are only 1.3 standard deviations away from the current best estimates.
And more recently (PDG 18, p. 9):
However, for the value of Higgs mass experimentally measured, the EW vacuum of the Higgs potential is most likely metastable. Indeed, the high energy evolution of shows that it becomes negative at energies GeV, with a broader range if the top quark mass exceeds its current measured value by 3σ. When this occurs, the SM Higgs potential develops an instability and the long term existence of the EW vacuum is challenged. This behavior may call for new physics at an intermediate scale before the instability develops, i.e., below M_Planck, otherwise, the electroweak vacuum remains metastable.
However quantum tunneling/vacuum decay is an intrinsically non-perturbative effect which needs careful treatment beyond perturbative quantum field theory (e.g. AFFS 17)
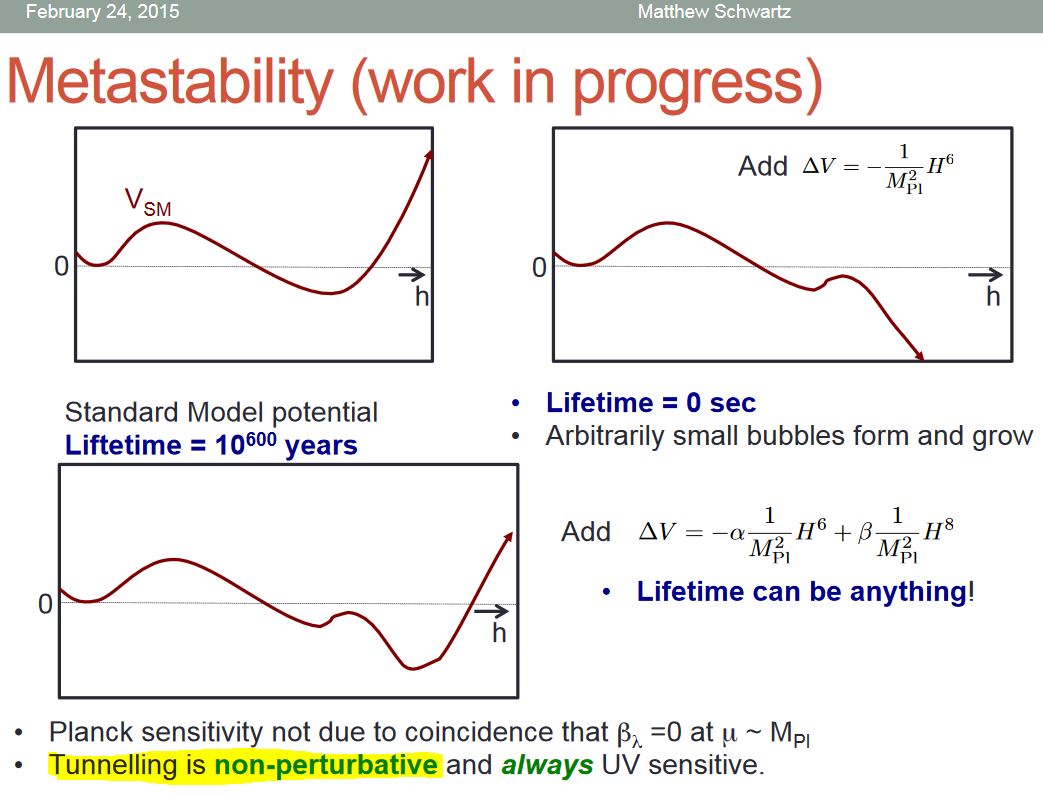
graphics grabbed form Schwartz 15, slide 44
Possible causes of the near criticality
Given, by the above discussion, that the parameters of the Higgs field are observed to be inside a special reason of their potential parameter space, it is natural to speculate that there is some mechanism that enforces or at least prefers this position.
In BDGGSSS 13, Section 5.2 is speculation that for dynamics over a landscape of vacua critical points may generally serve as attractors.
More specifically, Isidori-Pattori 17 claims that, under reasonable assumptions (including gauge coupling unification, but excluding “naturalness”) supersymmetric-extensions of the standard model of particle physics (MSSM) predict a parameter range for the top quark and Higgs field mass that is close to coinciding with the corresponding parameter space for Higgs field near criticality:
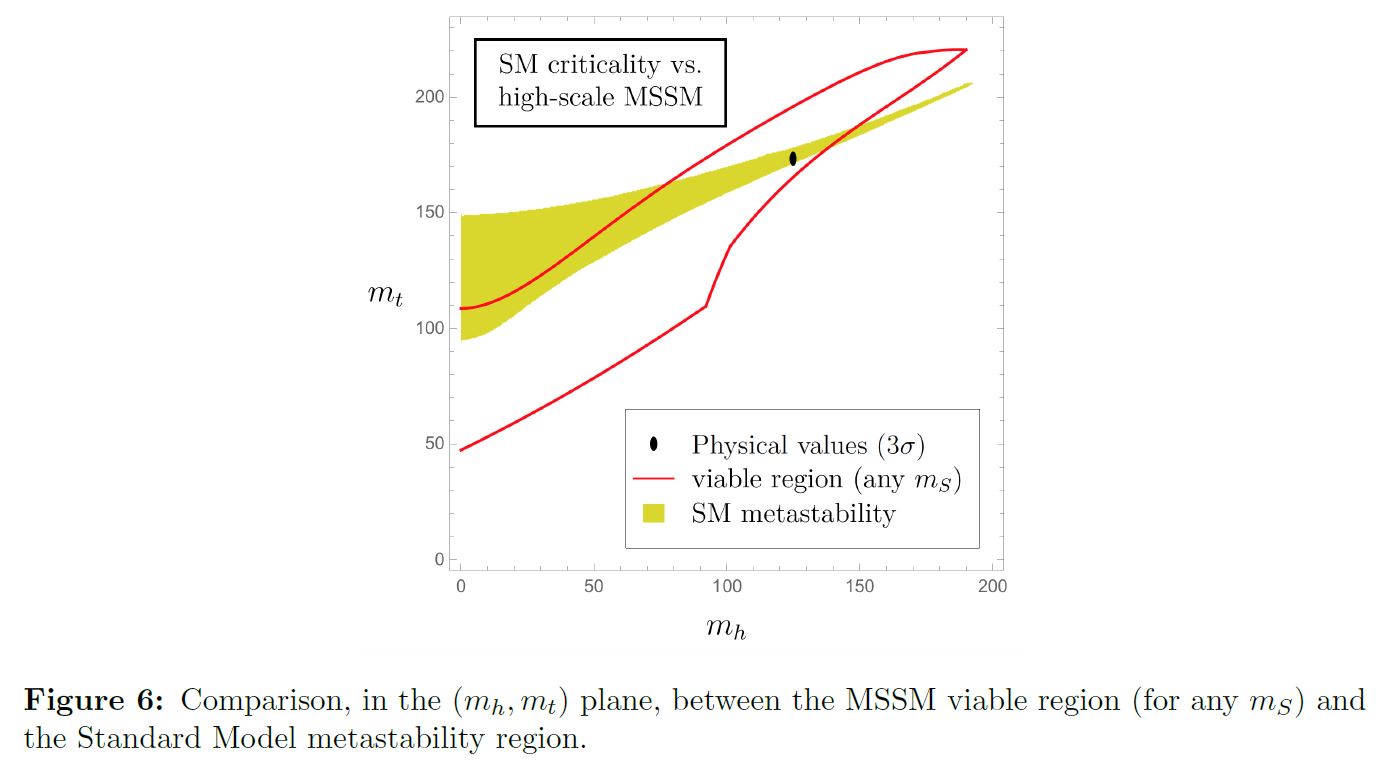
graphics grabbed from Isidori-Pattori 17
That supersymmetry, possibly in a G₂-MSSM, would be a natural mechanism behind the near criticality of the Higgs field was also claimed in Kane 18, “Clue 4”.
Cosmological instability?
However, it has been argued that an actual false vacuum of the Higgs is incompatible with cosmology, as due to vacuum fluctuations during inflation the vacuum decay would not have been avoided (EGR 07, HKSZ 14, EGMRSST 15, EKSYZ 16). In (BDGGSSS 13, section 7, Kane 18 , “Clue 4”) it was argued that this suggests a further principle which prevents the vacuum instability and that a natural such principle is supersymmetry. (This argument has a long history, see Gibbs 11b).
Asymptotic safety?
The near criticality of the Higgs field vacuum discussed above implies that the coefficient of the quartic part of the Higgs potential is close to zero after renormalization group flow (“RGE”) to around the Planck scale of about GeV (e.g. BDGGSSS 13, p. 17-18):
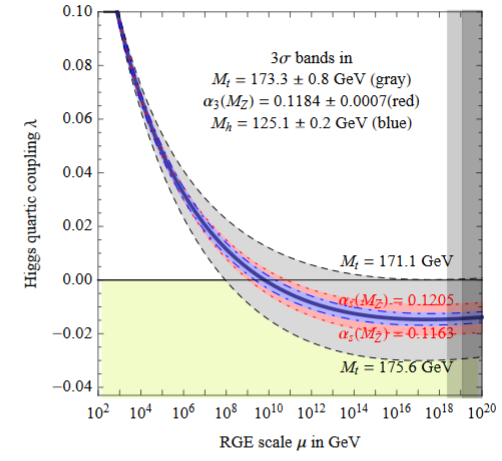
In fact also the beta function of the quartic coupling (i.e. its logarithmic derivative with respect to scale) is close to zero around the Planck scale of about GeV (BDGGSSS 13, p. 18):
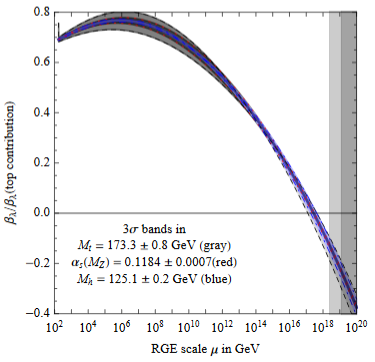
Earlier it has been suggested that this reflects the principle of asymptotic safety (Shaposhnikov-Wetterich 09). But this would mean that not only and its RGE-derivative vanish around the Planck scale, but that in fact all higher derivatives do, too (see e.g. Niedermaier 06, equation (1.5)) hence that asymptotes to zero. But this does not seem to be the case; in (BDGGSSS 13, p. 17-18) it says:
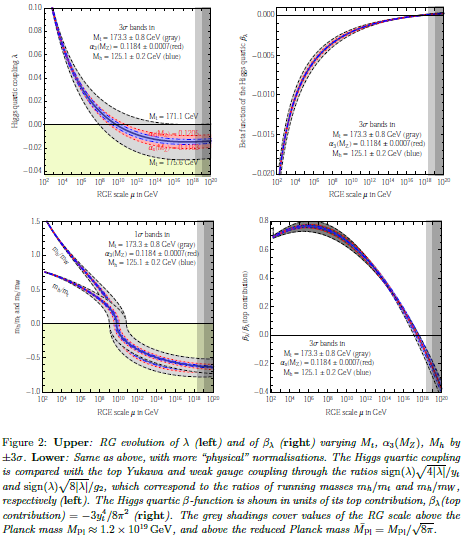
As shown in fig. 2 (upper right), the corresponding Higgs quartic beta-function vanishes at a scale of about - GeV. In order to quantify the degree of cancellation in the β-function, we plot in fig. 2 (lower right) in units of its pure top quark contribution. The vanishing of looks more like an accidental cancellation between various large contributions, rather than an asymptotic approach to zero.
Higgs inflation?
Starting with Jegerlehner 13 has been argued that the near-criticality of the Higgs potential is in fact consistent or even necessary for Higgs inflation to be a viable model. See Jegerlehner 18.
Models
There is no lack of proposals for realizing the Higgs field in various big schemes of mathematical structures modelling physics.
Gauge-Higgs unification
A mechanism, of gauge-Higgs unification (Manton 79, Hosotani 83) also known as the Hosotani mechanism (see Hosotani 12) refers to hypothetical models of particle physics where the Higgs field on 4d spacetimes arises as a component of a gauge field in higher dimensions, either after Kaluza-Klein compactification or by passage to a 4d asymptotic boundary in a Randall-Sundrum model or similar.
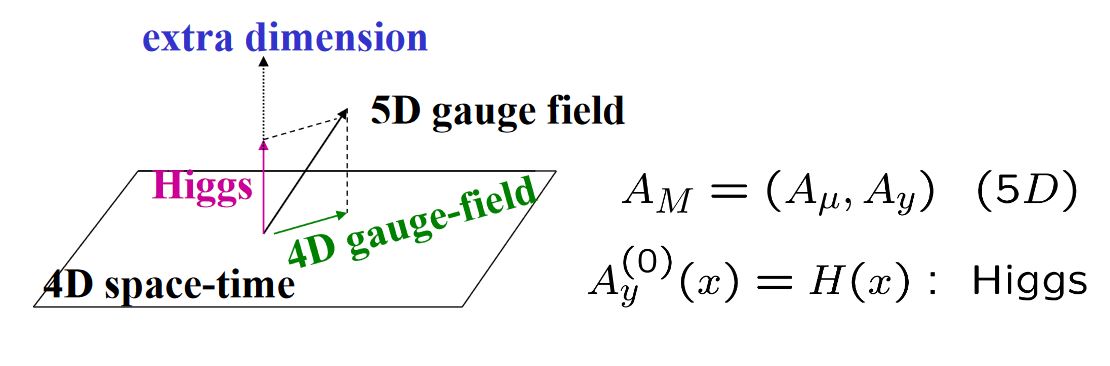
graphics grabbed from Lim 09
Gauge-Higgs unification is naturally combined with grand unification of gauge groups, whence one then also speaks of gauge-Higgs grand unification (e.g. Hosotani-Yamatsu 15)
Also the Connes-Lott models realize gauge-Higgs unification, in a non-commutative geometric KK-compactification.
In string theory
In string theory (see string phenomenology) a Higgs mechanism can arise in a variety of ways.
In intersecting D-brane models
Notably in intersecting D-brane models it arises naturally from brane recombination at intersections: (Cremades-Ibanez-Marchesano 02, section 7):
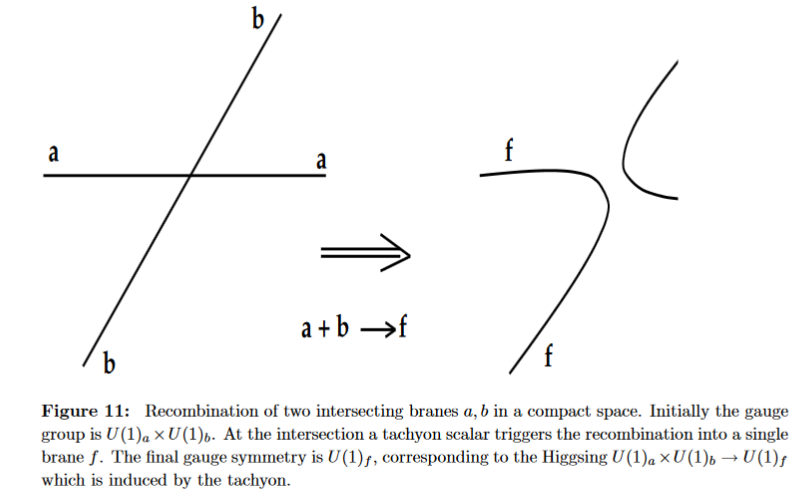
Further developments in Ibanez-Marchesano-Rabadan 01, Hebecker-Knochel-Weigand 13 and specifically via string field theory in HINSS 18.
For review see Ibanez-Uranga 12, fig 10.2:
In -MSSM
Discussion of the Higgs mechanism in the G₂-MSSM: Kane 11, Kane-Kumar-Lu-Zheng 11, for review see Kane 17, Kane 18
Other
-
in the technicolor model the Higgs field is not a fundamental particle but a compound of fermions. This realizes the Higgs effect entirely in ordinary gauge theory;
-
in Connes-Lott-Chamseddine-Barrett models it has been shown that the Higgs may be modeled as a component of the gauge bosons assuming that the KK-reduction is over a certain non-commutative space of classical dimension 0.
History
The Higgs mechanism was proposed in 1963-1964 by a fair number of authors essentially simultaneously, see the References below. The explicit prediction of the Higgs boson implied by this mechanism though seems to be solely due to (Higgs 64).
The Higgs boson (or at least something very much like it) was finally detected in 2013 at the LHC experiment.
So for the Higgs particle prediction and experimental detection lie apart by about 50 years. Compare maybe to the neutrino, which was predicted in 1930 and detected in 1956, about 26 years later.
Related concepts
standard model of particle physics and cosmology
| theory: | Einstein- | Yang-Mills- | Dirac- | Higgs |
|---|---|---|---|---|
| gravity | electroweak and strong nuclear force | fermionic matter | scalar field | |
| field content: | vielbein field | principal connection | spinor | scalar field |
| Lagrangian: | scalar curvature density | field strength squared | Dirac operator component density | field strength squared + potential density |
References
General
The original articles explaining what is now called the Higgs mechanism by spontaneous symmetry breaking were
-
P. Anderson, Plasmons, gauge invariance and mass, Physical Review 130: 439. (1963)
-
François Englert, Robert Brout, Broken Symmetry and the Mass of Gauge Vector Mesons, Physical Review Letters 13 (9): 321–23. (1964)
-
Gerald Guralnik, C. R. Hagen, ; T. W. B. Kibble, Global Conservation Laws and Massless Particles Physical Review (1964)
-
Peter Higgs, Broken Symmetries and the Masses of Gauge Bosons, Physical Review Letters 13 (16): 508–509. (1964)
While all these articles essentially describe the Higgs mechanism, apparently only the one by Peter Higgs explicitly points out that this mechanism predicts the existence of a new, then unobserved, boson, the one therefore now called the Higgs boson.
Review:
-
Particle Data Group, Review of particle physics, Status of Higgs Boson Physics, 2018 (pdf, pdf)
-
Antonio Pich, Electroweak Symmetry Breaking and the Higgs Boson, Acta Phys. Pol. B 47, 151 (2016) (arXiv:1512.08749)
-
Sally Dawson, Christoph Englert, Tilman Plehn, Higgs Physics: It ain’t over till it’s over, Physics Reports (arXiv:1808.01324)
-
Jochem Kip, Ronald Kleiss, The Higgs Mechanism with Diagrams: a didactic approach [arXiv:2404.08329]
(discussion via Feynman diagrams)
Review of the general theory of spontaneous symmetry breaking:
- Jeremy Bernstein, Spontaneous symmetry breaking, gauge theories, the Higgs mechanism and all that, Rev. Mod. Phys. 46, 7–48 (1974) (pdf)
The phenomenology of Higgs models is discussed in
- Marcela Carena, Howard E. Haber, Higgs Boson Theory and Phenomenology, Prog.Part.Nucl.Phys.50:63-152,2003 (arXiv:hep-ph/0208209)
Discussion in “string localized” AQFT and claim of derivation of the quartic form of the Higgs potential:
- Jens Mund, Karl-Henning Rehren, Bert Schroer, How the Higgs potential got its shape [arXiv:2209.06133]
Detection
Early discussion of the detection of a Higgs field of 125 GeV at LHC is in
-
Philip Gibbs, Seminar Watch (Higgs Special), Rumoured Higgs at 125 GeV and What Would a Higgs at 125 GeV Tell Us?, Prespacetime Journal, December 2011, Vol. 2 Issue 12 pp. 1899-1905 (web)
-
Martin Holthausen, Kher Sham Lim, Manfred Lindner, Planck Scale Boundary Conditions and the Higgs Mass, JHEP 1202 (2012) 037 (arXiv:1112.2415)
The official announcement of the detection at LHC is due to
-
G. Aad et al. (ATLAS Collaboration), Observation of a New Particle in the Search for the Standard Model Higgs Boson with the ATLAS Detector at the LHC, Phys. Lett. B 716, 1 (2012) (arXiv:1207.7214)
-
S. Chatrchyan et al. (CMS Collaboration), Observation of a New Boson at a Mass of 125 GeV with the CMS Experiment at the LHC, 716, 30 (2012) (arXiv:1207.7235)
-
G. Aad et al. (ATLAS Collaboration, CMS Collaboration), Combined Measurement of the Higgs Boson Mass in Collisions at and 8 TeV with the ATLAS and CMS Experiments, Phys. Rev. Lett. 114, 191803 (2015) (arXiv:1503.07589)
Vacuum (in-)stability
Before experimental observation of the Higgs mass at the LHC, the three possible outcomes for vacuum stability were analyzed in
-
John Ellis, J.R. Espinosa, Gian Giudice, A. Hoecker, A. Riotto, The Probable Fate of the Standard Model, Phys.Lett.B679:369-375,2009 (arXiv:0906.0954)
-
Philip Gibbs, What would a Higgs at 125 GeV tell us?, in Seminar Watch (Higgs Special), Rumoured Higgs at 125 GeV and What Would a Higgs at 125 GeV Tell Us?, Prespacetime Journal, December 2011, Vol. 2 Issue 12 pp. 1899-1905 (web)
More discussion of the near-criticality of the vacuum stability after the observation of the Higgs mass is due to
- Giuseppe Degrassi, Stefano Di Vita, Joan Elias-Miró, José R. Espinosa, Gian Giudice, Gino Isidori, Higgs mass and vacuum stability in the Standard Model at NNLO, J. High Energ. Phys. (2012) 2012: 98 (arrXiv:1205.6497, doi:10.1007/JHEP(2012)098)
with a more precise analysis due to
- A. V. Bednyakov, B. A. Kniehl, A. F. Pikelner, and O. L. Veretin, Stability of the Electroweak Vacuum: Gauge Independence and Advanced Precision, Phys. Rev. Lett. 115, 201802 (arXiv:1507.08833, doi:10.1103/PhysRevLett.115.201802)
Careful discussion of the stability issue under renormalization is in
- Anders Andreassen, William Frost, Matthew D. Schwartz, Consistent Use of the Standard Model Effective Potential, Phys. Rev. Lett. 113, 241801 (2014) (arXiv:1408.0292)
and with emphasis on non-perturbative effects in quantum tunneling/vacuum decay
- Anders Andreassen, David Farhi, William Frost, Matthew D. Schwartz, Precision decay rate calculations in quantum field theory, Phys. Rev. D 95, 085011 (2017) (arXiv:1604.06090)
Review includes
-
Alexander Kusenko, Are We on the Brink of the Higgs Abyss?, Physics 8, 108 (2015)
-
Sebastian Baum, On the metastability of the Standard Model, 2015 (pdf)
-
Holger Gies, Vacuum stability and the mass of the Higgs boson, 2015 (pdf)
-
Matthew Schwartz, Do we know if our universe is stable?, Rutgers Seminar 2015 (pdf)
-
Alessandro Strumia, Higgs and Vacuum (In)Stability, talk at GGI 2017 (pdf)
-
Anders Andreassen, William Frost, Matthew D. Schwartz, Scale Invariant Instantons and the Complete Lifetime of the Standard Model, Phys. Rev. D 97, 056006 (2018) (arXiv:1707.08124)
Speculation about what this near-criticality of the Higgs vacuum could be pointing to:
attractor mechanism in a landscape of vacua:
- Dario Buttazzo, Giuseppe Degrassi, Pier Paolo Giardino, Gian Giudice, Filippo Sala, Alberto Salvio, Alessandro Strumia, section 7 of Investigating the near-criticality of the Higgs boson, JHEP12(2013)089 (arXiv:1307.3536)
an supersymmetric-extension of the standard model of particle physics (e.g. MSSM, G₂-MSSM, …)
- Gino Isidori, Andrea Pattori, On the tuning in the plane: Standard Model criticality vs. High-scale SUSY, Physics Letters B Volume 782, 10 July 2018, Pages 551-558 (arXiv:1710.11060)
as well as Kane 18, “Clue 4”
and more generally in view of split supersymmetry:
- Gian Giudice, Alessandro Strumia, Probing High-Scale and Split Supersymmetry with Higgs Mass Measurements, Nuclear Physics B Volume 858, Issue 1, 1 May 2012, Pages 63-83 (arXiv:1108.6077)
Arguments that a false Higgs vacuum is incompatible with cosmological evolution (inflation) include the following:
-
J.R. Espinosa, Gian Giudice, A. Riotto, Cosmological implications of the Higgs mass measurement, JCAP 0805:002, 2008 (arXiv:0710.2484)
-
Anson Hook, John Kearney, Bibhushan Shakya, Kathryn M. Zurek, Probable or Improbable Universe? Correlating Electroweak Vacuum Instability with the Scale of Inflation, J. High Energ. Phys. (2015) 2015: 61 (arXiv:1404.5953)
-
Jose R. Espinosa, Gian Giudice, Enrico Morgante, Antonio Riotto, Leonardo Senatore, Alessandro Strumia, Nikolaos Tetradis, The cosmological Higgstory of the vacuum instability (arXiv:1505.04825)
-
William E. East, John Kearney, Bibhushan Shakya, Hojin Yoo, Kathryn M. Zurek, Spacetime Dynamics of a Higgs Vacuum Instability During Inflation, Phys. Rev. D 95, 023526 (2017) (arXiv:1607.00381)
But see
- Mark P. Hertzberg, Mudit Jain, Explanation for why the Early Universe was Stable and Dominated by the Standard Model, JCAP 2020 (arXiv:1911.04648)
for a possible solution by strong interaction between the Higgs field and the inflaton.
An interpretation in terms of asymptotic safety:
- Mikhail Shaposhnikov, Christof Wetterich, Asymptotic safety of gravity and the Higgs boson mass, Phys. Lett. B 683 (2010) 196 [arXiv:0912.0208]
Proposals for further experiments:
- Roberto Franceschini, Alessandro Strumia, Andrea Wulzer, The collider landscape: which collider for establishing the SM instability?, Journal of High Energy Physics 2022 229 (2022) [arXiv:2203.17197, doi:10.1007/JHEP08(2022)229]
See also:
-
Thomas Steingasser, David I. Kaiser, Higgs Criticality beyond the Standard Model [arXiv:2307.10361]
-
Gudrun Hiller, Tim Höhne, Daniel F. Litim, Tom Steudtner, Vacuum Stability in the Standard Model and Beyond [arXiv:2401.08811]
-
Thomas Steingasser, Higgs criticality in and beyond the Standard Model [arXiv:2405.02415]
-
Alessandro Strumia: The Higgs boson and the possible instability in its potential, talk at #ICBS2024 [video]
Diphoton decay
On renormalization of the Higgs field‘s diphoton decay using causal perturbation theory:
- Pawel Duch, Michael Duetsch, Jose Gracia-Bondia, Diphoton decay of the higgs from the Epstein–Glaser viewpoint (arXiv:2011.12675)
Gauge-Higgs unification
Discussion of gauge-Higgs unification:
The mechanism is due to
-
Nicholas Manton, A new six-dimensional approach to the Weinberg-Salam model, Nuclear Physics B Volume 158, Issue 1, 8 October 1979, Pages 141-153 (doi:10.1016/0550-3213(79)90192-5)
-
Yutaka Hosotani, Dynamical Mass Generation by Compact Extra Dimensions, Phys. Lett. 126B (1983) 309-313 (spire:188768, doi:10.1016/0370-2693(83)90170-3)
-
Yutaka Hosotani, Dynamics of non-integrable phases and gauge symmetry breaking, Annals of Physics Volume 190, Issue 2, March 1989, Pages 233-253 (doi:10.1016/0003-4916(89)90015-8)
and was revived with:
- H. Hatanaka, T. Inami, C.S. Lim, The Gauge Hierarchy Problem and Higher Dimensional Gauge Theories, Mod. Phys. Lett. A13 (1998) 2601-2612 (arXiv:hep-th/9805067)
Review:
- Yutaka Hosotani, Gauge-Higgs Unification Approach, AIP Conference Proceedings 1467, 208 (2012) (arXiv:1206.0552)
See also:
-
Naoyuki Haba, Kazunori Takenaga, Toshifumi Yamashita, Higgs mass in the gauge-Higgs unification, Phys. Lett. B615 (2005) 247-256 (arXiv:hep-ph/0411250)
-
C. S. Lim, Precision Tests and CP Violation in Gauge-Higgs Unification, 2009 (slides pdf)
Discussion of gauge-Higgs unification in Spin(11)-GUT (“SO(11)-GUT”):
-
Yutaka Hosotani, Naoki Yamatsu, Gauge–Higgs grand unification, Progress of Theoretical and Experimental Physics, Volume 2015, Issue 11, November 2015 (arXiv:1504.03817, doi:10.1093/ptep/ptw116)
-
Atsushi Furui, Yutaka Hosotani, Naoki Yamatsu, Toward Realistic Gauge-Higgs Grand Unification, Progress of Theoretical and Experimental Physics, Volume 2016, Issue 9, September 2016, 093B01 (arXiv:1606.07222)
-
Yutaka Hosotani, Gauge-Higgs EW and Grand Unification, International Journal of Modern Physics AVol. 31, No. 20n21, 1630031 (2016) (arXiv:1606.08108)
-
Yutaka Hosotani, New dimensions from gauge-Higgs unification (arXiv:1702.08161)
-
Yutaka Hosotani, Naoki Yamatsu, Electroweak Symmetry Breaking and Mass Spectra in Six-Dimensional Gauge-Higgs Grand Unification (arXiv:1710.04811)
Discussion of gauge-Higgs unification in Spin(11)-GUT (“SO(11)-GUT”):
-
S. Rajpoot and P. Sithikong, Implications of the gauge symmetry for grand unification, Phys. Rev. D 23, 1649 (1981) (doi:10.1103/PhysRevD.23.1649)
-
Takaaki Nomura, Joe Sato, Standard(-like) Model from an Grand Unified Theory in six-dimensions with extra-space, Nucl.Phys.B811:109-122, 2009 (arXiv:0810.0898)
-
Takaaki Nomura, Physics beyond the standard model with extra-space, 2009 (pdf, pdf)
-
Cheng-Wei Chiang, Takaaki Nomura, Joe Sato, Gauge-Higgs unification models in six dimensions with extra space and GUT gauge symmetry (arXiv:1109.5835)
In string theory
Discussion of the Higgs field from intersecting D-brane models is due to
-
Luis Ibáñez, Fernando Marchesano, R. Rabadan, section 7 of Getting just the Standard Model at Intersecting Branes, JHEP 0111:002, 2001 (arXiv:hep-th/0105155)
-
D. Cremades, Luis Ibáñez, Fernando Marchesano, Intersecting brane models of particle physics and the Higgs mechanism, JHEP, 0207, 022 2002 (arXiv:hep-th/0203160)
-
Arthur Hebecker, Alexander K. Knochel, Timo Weigand, The Higgs mass from a String-Theoretic Perspective, Nucl.Phys. B874 (2013) 1-35 (arXiv:1304.2767)
-
Manami Noumi Hashi, Hiroshi Isono, Toshifumi Noumi, Gary Shiu, Pablo Soler, Higgs Mechanism in Nonlocal Field Theories, JHEP08 (2018) 064 (arXiv:1805.02676)
Discussion of the Higgs mechanism in the G₂-MSSM and related models is due to
-
Gordon Kane, String theory and generic predictions for our world – superpartner masses, LHC signatures, dark matter, EWSB, cosmological history of universe, etc, talk at String phenomenology 2011, August 2011 (pdf)
-
Gordon Kane, Piyush Kumar, Ran Lu, Bob Zheng, Higgs Mass Prediction for Realistic String/M Theory Vacua, Phys. Rev. D 85, 075026 (arXiv:1112.1059)
(a useful informed comment is here)
and related to the issue of the vacuum stability in
- Gordon Kane, Exciting Implications of LHC Higgs Boson Data (arXiv:1802.05199)
which is based on
- Gordon Kane, String theory and the real world, Morgan & Claypool, 2017 (doi:0.1088/978-1-6817-4489-6)
See also
-
Lawrence J. Hall, Yasunori Nomura, Grand Unification and Intermediate Scale Supersymmetry, JHEP02 (2014) 129 (arXiv:1312.6695)
-
Lawrence J. Hall, Yasunori Nomura, Satoshi Shirai, Grand Unification, Axion, and Inflation in Intermediate Scale Supersymmetry (arXiv:1403.8138)
-
David Dunsky, Lawrence J. Hall, Keisuke Harigaya, Dark Matter Detection, Standard Model Parameters, and Intermediate Scale Supersymmetry (arXiv:2011.12302)
Discussion in holographic QCD:
-
Domenec Espriu, Alisa Katanaeva, Composite Higgs Models: a new holographic approach (arXiv:1812.01523)
-
Johanna Erdmenger, Nick Evans, Werner Porod, Konstantinos Rigatos, Gauge/gravity dual dynamics for the strongly coupled sector of composite Higgs models, JHEP 58 (2021) [arXiv:2010.10279, doi:10.1007/JHEP02(2021)058]
Discussion in heterotic string theory:
- Steven Abel, Keith Dienes, Calculating the Higgs Mass in String Theory (arXiv:2106.04622)
Last revised on May 14, 2025 at 17:58:52. See the history of this page for a list of all contributions to it.