nLab p-adic AdS/CFT correspondence
Context
Duality in string theory
general mechanisms
-
electric-magnetic duality, Montonen-Olive duality, geometric Langlands duality
string-fivebrane duality
string-QFT duality
QFT-QFT duality:
-
effective QFT incarnations of open/closed string duality,
relating (super-)gravity to (super-)Yang-Mills theory:
-
Seiberg duality (swapping NS5-branes)
Arithmetic geometry
- natural number, integer number, rational number, real number, irrational number, complex number, quaternion, octonion, adic number, cardinal number, ordinal number, surreal number
-
transfinite arithmetic, cardinal arithmetic, ordinal arithmetic
-
prime field, p-adic integer, p-adic rational number, p-adic complex number
arithmetic geometry, function field analogy
Contents
Idea
A version of the AdS/CFT correspondence (specifically: AdS3/CFT2 duality) for p-adic physics, obtained by passing on the conformal field theory-side from the complex geometry, hence (via GAGA)algebraic geometry of 2d CFT to arithmetic geometry over p-adic numbers, and on the string theory-side to p-adic string theory (?)
Here the arithmetic geometry-version of the bulk AdS spacetime is identified with the Bruhat-Tits tree for the projective general linear group :
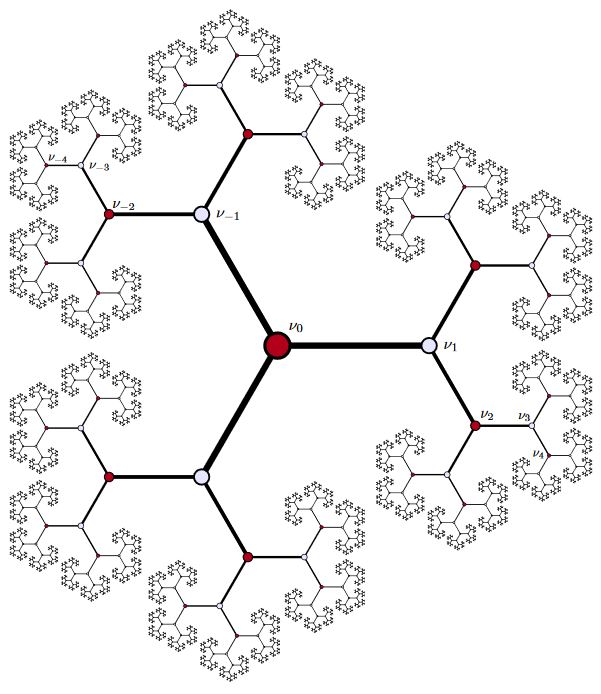
graphics from Casselman 14
This may be regarded (at some finite depth truncation) as a tensor network state:
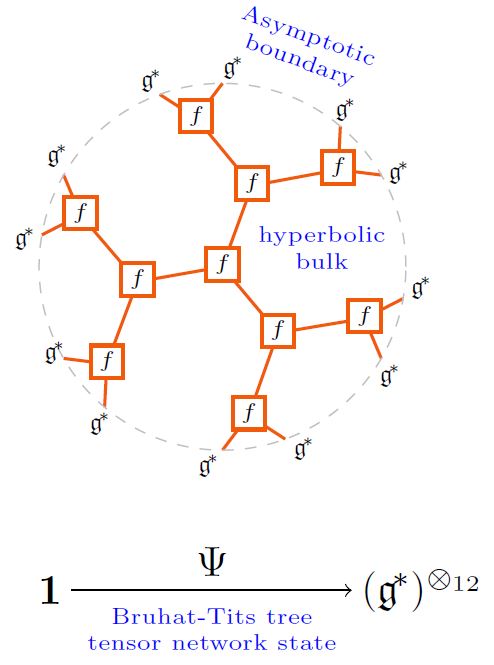
graphics from Sati-Schreiber 19c
(As in HMSS 16, HLM 19. But maybe one wants the Poincaré-dual networks, instead, as in HMPS 18?)
There is the suggestion that BTZ black holes are encoded by networks that look like Bruhat-Tits trees towards the boundaries and like matrix product states towards the interior:
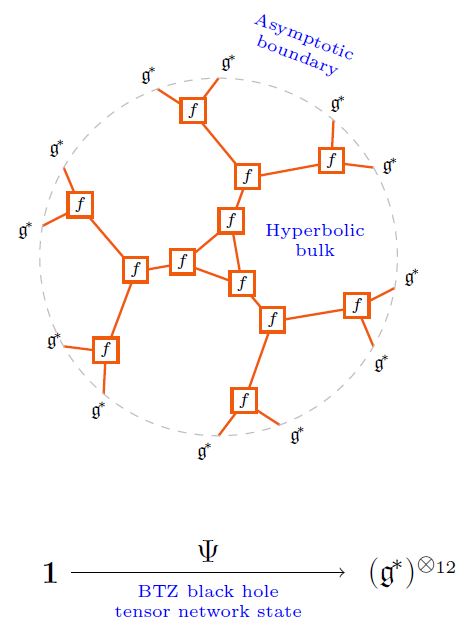
(As in ESZ 19.)
Related concepts
References
Suggestion to identify the Bruhat-Tits tree with anti de Sitter spacetime in the p-adic AdS/CFT correspondence:
-
Steven Gubser, Johannes Knaute, Sarthak Parikh, Andreas Samberg, Przemek Witaszczyk, -adic AdS/CFT, Communications in Mathematical Physics volume 352, pages 1019–1059 (2017) (arXiv:1605.01061)
-
Steven Gubser, Sarthak Parikh, Geodesic bulk diagrams on the Bruhat-Tits tree (arXiv:1704.01149)
-
Yuri Manin, Matilde Marcolli Holography principle and arithmetic of algebraic curves, Adv. Theor. Math. Phys. 5 (2001), no. 3, 617–650 (arXiv:hep-th/0201036)
Relation to tensor networks:
-
Matthew Heydeman, Matilde Marcolli, Ingmar Saberi, Bogdan Stoica, Tensor networks, -adic fields, and algebraic curves: arithmetic and the correspondence (arXiv:1605.07639)
-
Arpan Bhattacharyya, Ling-Yan Hung, Yang Lei, Wei Li, Tensor network and (-adic) AdS/CFT, JHEP 1801 (2018) 139 (arXiv:1703.05445)
-
Ling-Yan Hung, Wei Li, Charles M. Melby-Thompson, -adic CFT is a holographic tensor network (arXiv:1902.01411)
-
Lin Chen, Xirong Liu, Ling-Yan Hung, Emergent Einstein Equation in p-adic CFT Tensor Networks (arXiv:2102.12022)
-
Lin Chen, Xirong Liu, Ling-Yan Hung, Bending the Bruhat-Tits Tree I:Tensor Network and Emergent Einstein Equations (arXiv:2102.12023)
-
Lin Chen, Xirong Liu, Ling-Yan Hung, Bending the Bruhat-Tits Tree II: the p-adic BTZ Black hole and Local Diffeomorephism on the Bruhat-Tits Tree (arXiv:2102.12024)
-
Feng Qu, The effective field theory on a finite boundary of the Bruhat-Tits tree (arXiv:2103.02882)
Including spinors:
- Steven Gubser, Christian Jepsen, Brian Trundy, Spin in -adic AdS/CFT, Journal of Physics A: Mathematical and Theoretical, Volume 52, Number 14 (arXiv:1811.02538)
Including BTZ black holes:
-
Matthew Heydeman, Matilde Marcolli, Sarthak Parikh, Ingmar Saberi, Nonarchimedean Holographic Entropy from Networks of Perfect Tensors (arXiv:1812.04057)
-
Stephen Ebert, Hao-Yu Sun, Meng-Yang Zhang, Probing holography in -adic CFT (arXiv:1911.06313)
An expository account is given in
- Ingmar Saberi, Holography and local fields, (arXiv:1801.04942)
Proposed realization of aspects of p-adic AdS/CFT correspondence in solid-state physics:
- Gregory Bentsen, Tomohiro Hashizume, Anton S. Buyskikh, Emily J. Davis, Andrew J. Daley, Steven Gubser, Monika Schleier-Smith, Treelike interactions and fast scrambling with cold atoms, Phys. Rev. Lett. 123, 130601 (2019) (arXiv:1905.11430)
See also:
- Feng Qu, -adic AdS/CFT on subspaces of the Bruhat-Tits tree [arXiv:2402.03730]
Last revised on March 17, 2025 at 00:28:37. See the history of this page for a list of all contributions to it.