nLab AGT correspondence
Context
Duality in string theory
general mechanisms
-
electric-magnetic duality, Montonen-Olive duality, geometric Langlands duality
string-fivebrane duality
string-QFT duality
QFT-QFT duality:
-
effective QFT incarnations of open/closed string duality,
relating (super-)gravity to (super-)Yang-Mills theory:
-
Seiberg duality (swapping NS5-branes)
Functorial Quantum field theory
Algebraic Quantum Field Theory
algebraic quantum field theory (perturbative, on curved spacetimes, homotopical)
Concepts
quantum mechanical system, quantum probability
interacting field quantization
Theorems
States and observables
Operator algebra
Local QFT
Perturbative QFT
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
Idea
The AGT correspondence (AGT 09) is a relation between
-
the instanton-partition function of -N=2 D=4 super Yang-Mills theory (Nekrasov’s partition function, e.g. Szabo 15 (2.1))
-
the conformal blocks of Liouville theory on an -punctured Riemann surface of genus
Here the idea is that is the super Yang-Mills theory obtained by compactifying the worldvolume 6d (2,0)-supersymmetric QFT of two M5-branes, see at N=2 D=4 super Yang-Mills theory, the section Construction by compactification). This method generalizes a bit beyond super Yang-Mills, to class S.
In particular, the N=2 D=4 super Yang-Mills theory is a quiver gauge theory and the correspondence matches the shape of its quiver-diagram to the genus and punctures of the Riemann surface:
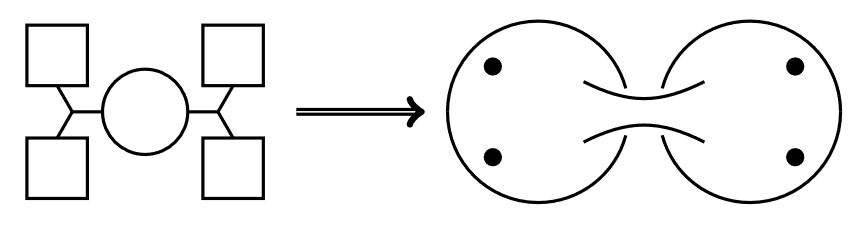
More generally, this construction yields something like a decomposition of the 6d (2,0)-superconformal QFT into a 2d SCFT “with values in 4d SYM field theory” (e.g. Tachikawa 10, slide 25 (33 of 54)). Hence composition with any kind of suitable invariant of the 4d field theories yields an actual 2d SCFT, for instance taking the superconformal index in 4d yields a 2d TQFT (GPRR 10). In this picture of “4d-SYM field theory-valued 2d SCFT” one has the following correspondences:
-
the complex structure in 2d is the coupling constants and theta angles etc in the 4d super Yang-Mills theory;
-
the mapping class group (large conformal transformations) in 2d is the (generalized) S-duality of the 4d theory.
Related concepts
Wrapping the M5-brane on a 3-manifold instead yields: 3d-3d correspondence.
References
A 2d SCFT argued to describe the KK-compactification of the M5-brane on a 4-manifold (specifically: a complex surface) originates with
- Juan Maldacena, Andrew Strominger, Edward Witten, Black Hole Entropy in M-Theory, JHEP 9712:002, 1997 (arXiv:hep-th/9711053)
The origin of the AGT correspondence is:
-
Davide Gaiotto, dualities, JHEP 08 (2012) 034 [arXiv:0904.2715]
-
Luis Alday, Davide Gaiotto, Yuji Tachikawa, Liouville Correlation Functions from Four-dimensional Gauge Theories, Lett.Math.Phys.91:167-197, 2010 (arXiv:0906.3219)
-
Davide Gaiotto, Gregory Moore, Andrew Neitzke, Wall-crossing, Hitchin systems, and the WKB approximation, Advances in Mathematics 234 (2013) 239–403 (arXiv:0907.3987 doi)
The 2d TQFT obtained from this by forming the 4d index is discussed in
- Abhijit Gadde, Elli Pomoni, Leonardo Rastelli, Shlomo S. Razamat, S-duality and 2d Topological QFT, JHEP 1003:032, 2010 (arXiv:0910.2225)
Relation of the AGT-correspondence to the D=6 N=(2,0) SCFT
-
Benjamin Assel, Sakura Schafer-Nameki, Jin-Mann Wong, M5-branes on : Nahm’s Equations and 4d Topological Sigma-models, J. High Energ. Phys. (2016) 2016: 120 (arxiv:1604.03606)
(relating to the moduli space of monopoles)
and to the 3d-3d correspondence:
-
Clay Cordova, Daniel Jafferis, Toda Theory From Six Dimensions, J. High Energ. Phys. (2017) 2017: 106 (arxiv:1605.03997)
-
Sam van Leuven, Gerben Oling, Generalized Toda Theory from Six Dimensions and the Conifold, J. High Energ. Phys. (2017) 2017: 50 (arxiv:1708.07840)
Brief surveys include
-
Yuji Tachikawa, M5-branes, 4d gauge theory and 2d CFT, 2010 (pdf)
-
Abhijit Gadde, Dualities and 2d TQFT 2012 (pdf)
-
Nikolay Bovev, New SCFTs from wrapped branes, 2013 (pdf)
-
Giulio Bonelli, Variations on AGT Correspondence, 2013 (pdf)
-
Masato Taki, String Theory as an Attempt of PolyMathematics, talk at 2016.4/28 iTHES-AIMR-IIS (pdf)
More detailed review is in
-
Rober Rodger, A pedagogical introduction to the AGT conjecture, Master Thesis Utrecht (2013) (pdf)
-
Richard Szabo, gauge theories, instanton moduli spaces and geometric representation theory, Journal of Geometry and Physics Volume 109, November 2016, Pages 83-121 (arXiv:1507.00685)
-
Bruno Le Floch, A slow review of the AGT correspondence, J. Phys. A: Math. Theor. 55 (2022) 353002 (doiarXiv:2006.14025)
See also
-
Alexander Belavin, M. A. Bershtein, B. L. Feigin, A. V. Litvinov, G. M. Tarnopolsky, Instanton moduli spaces and bases in coset conformal field theory (arxiv/1111.2803)
-
Volker Schomerus, Paulina Suchanek, Liouville’s imaginary shadow (arxiv/1210.1856)
-
A.Mironov, A.Morozov, The power of Nekrasov functions (arxiv/0908.2190)
-
D. Galakhov, A. Mironov, A. Morozov, S-duality as a beta-deformed Fourier transform (arxiv/1205.4998)
-
A. Mironov, Spectral duality in integrable systems from AGT conjecture (arxiv/1204.0913)
-
A. Belavin, V. Belavin, AGT conjecture and integrable structure of conformal field theory for , Nucl.Phys.B850:199-213 (2011) (arxiv/1102.0343)
-
A. Belavin, V. Belavin, M. Bershtein, Instantons and 2d Superconformal field theory (arxiv/1106.4001)
-
Kazunobu Maruyoshi, Quantum integrable systems, matrix models, and AGT correspondence, seminar (slides pdf)
-
Giulio Bonelli, Alessandro Tanzini, Hitchin systems, N=2 gauge theories and W-gravity (arxiv/0909.4031)
-
Giulio Bonelli, Kazunobu Maruyoshi, Alessandro Tanzini, Quantum Hitchin systems via beta-deformed matrix models (arxiv/1104.4016)
-
Oscar Chacaltana, Jacques Distler, Tinkertoys for Gaiotto Duality, JHEP 1011:099,2010, (arXiv:1008.5203)
-
Satoshi Nawata, Givental J-functions, Quantum integrable systems, AGT relation with surface operator (arXiv/1408.4132)
The AGT correspondence is treated with the help of a Riemann-Hilbert problem in
-
G. Vartanov, Jörg Teschner, Supersymmetric gauge theories, quantization of moduli spaces of flat connections, and conformal field theory (arxiv/1302.3778)
-
Andrei Mironov, A. Morozov, Superintegrability as the hidden origin of Nekrasov calculus [arXiv:2207.08242]
Proof of the AGT conjecture in special cases:
-
Andrei Mironov, Andrey Morozov, Sh. Shakirov, A direct proof of AGT conjecture at , JHEP 1102:067 (2011) [arXiv:1012.3137, doi:10.1007/JHEP02(2011)067]
-
Qing-Jie Yuan, Shao-Ping Hu, Zi-Hao Huang, Kilar Zhang, A proof of An AGT conjecture at [arXiv:2305.11839]
-
Qian Shen, Zi-Hao Huang, Shao-Ping Hu, Qing-Jie Yuan, Kilar Zhang, Proof of 5D AGT conjecture at [arXiv:2405.13676]
See also:
- Leszek Hadasz, Błażej Ruba, Decomposition of highest weight representations for generic level and equivalence between two dimensional CFT models [arXiv:2312.14695]
Last revised on May 24, 2024 at 05:42:57. See the history of this page for a list of all contributions to it.