nLab duality between M/F-theory and heterotic string theory
This entry is about M-theory/F-theory compactified on K3-surfaces. For M-theory on MO9-planes see instead at Hořava-Witten theory.
Context
Duality in string theory
general mechanisms
-
electric-magnetic duality, Montonen-Olive duality, geometric Langlands duality
string-fivebrane duality
string-QFT duality
QFT-QFT duality:
-
effective QFT incarnations of open/closed string duality,
relating (super-)gravity to (super-)Yang-Mills theory:
-
Seiberg duality (swapping NS5-branes)
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
Idea
A duality in string theory. The non-perturbative enhancement of duality between heterotic and type II string theory:
F-theory “KK-compactified” on an elliptically fibered K3 with a section is supposed to be equivalent to heterotic string theory KK-compactified on a 2-torus.
More generally, F-theory on a complex -dimensional fibered with elliptic K3-fibers is supposed to be equivalent to heterotic string theory on an elliptically fibered Calabi-Yau manifold of complex dimension .
A detailed discussion of the equivalence of the respective moduli spaces is originally due to (Friedman-Morgan-Witten 97). A review of this is in (Donagi 98).
From the abstract of (Donagi 98).
The heterotic string compactified on an -dimensional elliptically fibered Calabi-Yau is conjectured to be dual to F-theory compactified on an -dimensional Calabi-Yau , fibered over the same base with elliptic K3 fibers. In particular, the moduli of the two theories should be isomorphic. The cases most relevant to the physics are , , , i.e. the compactification is to dimensions , or respectively. Mathematically, the richest picture seems to emerge for , where the moduli space involves an analytically integrable system whose fibers admit rather different descriptions in the two theories.
Aspects
Singular locus of the elliptic fibration and 24 D7-branes
In passing from M-theory to type IIA string theory, the locus of any Kaluza-Klein monopole in 11d becomes the locus of D6-branes in 10d. The locus of the Kaluza-Klein monopole in turn (as discussed there) is the locus where the -circle fibration degenerates. Hence in F-theory this is the locus where the fiber of the -elliptic fibration degenerates to the nodal curve. Since the T-dual of D6-branes are D7-branes, it follows that D7-branes in F-theory “are” the singular locus of the elliptic fibration.
Now an elliptically fibered complex K3-surface
may be parameterized via the Weierstrass elliptic function as the solution locus of the equation
for , with a polynomial of degree 8 and of degree twelve. The j-invariant of the complex elliptic curve which this parameterizes for given is
The poles of the j-invariant correspond to the nodal curve, and hence it is at these poles that the D7-branes are located.
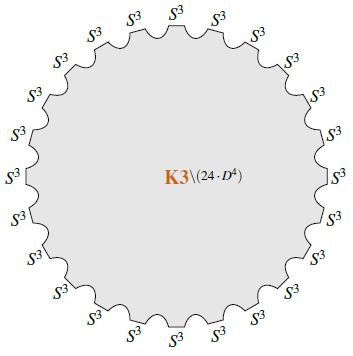
Since the order of the poles is 24 (the polynomial degree of the discriminant , see at elliptically fibered K3-surface – singular points) there are necessarily 24 D7-branes (Sen 96, page 5, Sen 97b, see also Morrison 04, sections 8 and 17, Denef 08, around (3.41), Douglas-Park-Schnell 14).
Under T-duality this translates to 24 D6-branes in type IIA string theory on K3 (Vafa 96, Footnote 2 on p. 6).
Notice that the net charge of these 24 D7-branes is supposed to vanish, due to S-duality effects (e.g. Denef 08, below (3.41)).
(This reminds one of the situation for the third stable homotopy group of spheres…)
For analogous discussion of 24 NS5-branes in heterotic string theory on K3 see Schwarz 97, around p. 50.
For more see at 24 branes transverse to K3.
From M-branes to F-branes to heterotic strings and NS5-branes
from M-branes to F-branes: superstrings, D-branes and NS5-branes
(e.g. Johnson 97, Blumenhagen 10)
Non-reducible heterotic -gauge backgrounds
There are some F-theory backgrounds whose supposed dual in heterotic string theory involves an E8-principal connection which is not reducible to SemiSpin(16) (Distler-Sharpe 10, section 5), while in fact the traditional construction of the heterotic worldsheet theory only covers this case. In (Distler-Sharpe 10, section 7-8) it is argued that therefore a more general formulation of heterotic string theory needs to involve parameterized WZW models. See also at heterotic string – Properties – General gauge backgrounds and parameterized WZW models.
Related concepts
F-theory KK-compactified on elliptically fibered complex analytic fiber
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| F-theory | F-theory on CY2 | F-theory on CY3 | F-theory on CY4 | F-theory on CY5 |
References
For type IIA and M-theory
The conjectured duality between type IIA string theory KK-compactified on K3 times an n-torus and heterotic string theory on the -torus is originally due to
-
Chris Hull, Paul Townsend, section 6 of: Unity of Superstring Dualities, Nucl. Phys. B438:109-137, 1995 (arXiv:hep-th/9410167)
-
Edward Witten, section 4 of: String Theory Dynamics In Various Dimensions, Nucl. Phys. B443:85-126, 1995 (arXiv:hep-th/9503124)
-
Wolfgang Lerche, On the Heterotic/F-Theory Duality in Eight Dimensions, In: Baulieu L., Green M., Picco M., Windey P. (eds.) Progress in String Theory and M-Theory, NATO Science Series (Series C: Mathematical and Physical Sciences), vol 564. Springer 2001 (arXiv:hep-th/9910207, doi:10.1007/978-94-010-0852-5_2)
Review:
-
Paul Aspinwall, David Morrison, String Theory on K3 Surfaces, in Brian Greene, Shing-Tung Yau (eds.), Mirror Symmetry II, International Press, Cambridge, 1997, pp. 703-716 (arXiv:hep-th/9404151)
-
Paul Aspinwall, K3 Surfaces and String Duality, in Shing-Tung Yau (ed.): Differential geometry inspired by string theory 1-95 (arXiv:9611137 spire:426102)
Further discussion:
-
Paul Aspinwall, Enhanced Gauge Symmetries and K3 Surfaces, Phys.Lett. B357 (1995) 329-334 (arXiv:hep-th/9507012)
-
Eric Bergshoeff, C. Condeescu, G. Pradisi, F. Riccioni, Heterotic-Type II duality and wrapping rules, JHEP12(2013)057 (arXiv:1311.3578)
Specifically in relation to the putative K-theory-classification of D-brane charge:
- Inaki Garcia-Etxebarria, Angel Uranga, From F/M-theory to K-theory and back, JHEP 0602:008,2006 (arXiv:hep-th/0510073)
Specifically in M-theory on G₂-manifolds:
-
Michael Atiyah, Edward Witten section 6.4 of -Theory dynamics on a manifold of -holonomy, Adv. Theor. Math. Phys. 6 (2001) (arXiv:hep-th/0107177)
-
Bobby Acharya, Alex Kinsella, David Morrison, Non-Perturbative Heterotic Duals of M-Theory on Orbifolds (arXiv:2106.03886)
Specifically in relation to Moonshine:
- Miranda Cheng, Sarah M. Harrison, Roberto Volpato, Max Zimet, K3 String Theory, Lattices and Moonshine (arXiv:1612.04404)
For F-theory
Discussion for F-theory includes
-
David Morrison, Cumrun Vafa, Compactifications of F-Theory on Calabi–Yau Threefolds – I, Nucl. Phys. B473 (1996) 74-92 (arXiv:hep-th/9602114)
-
David Morrison, Cumrun Vafa, Compactifications of F-Theory on Calabi–Yau Threefolds – II, Nucl. Phys. B476:437-469, 1996 (arXiv:hep-th/9603161)
-
Ashoke Sen, F-theory and Orientifolds (arXiv:hep-th/9605150)
-
Robert Friedman, John Morgan, Edward Witten, Vector Bundles And F Theory, Commun.Math.Phys.187:679-743, 1997 (arXiv:hep-th/9701162)
-
Paul Aspinwall, M-Theory Versus F-Theory Pictures of the Heterotic String, Adv.Theor.Math.Phys.1:127-147, 1998 (arXiv:hep-th/9707014)
Review of (Friedman-Morgan-Witten 97) is in
-
Ron Donagi, ICMP lecture on heterotic/F-theory duality (arXiv:hep-th/9802093)
-
Björn Andreas, Heterotic/F-theory duality, PhD thesis (pdf)
with more details in
- Ron Donagi, Eyal Markman, Spectral curves, algebraically completely integrable Hamiltonian systems, and moduli of bundles (arXiv:alg-geom/9507017)
The issue with non-reducible -gauge connections is highligted in
- Jacques Distler, Eric Sharpe, section 5 of Heterotic compactifications with principal bundles for general groups and general levels, Adv. Theor. Math. Phys. 14:335-398, 2010 (arXiv:hep-th/0701244)
On a subtlety in the application of the Narasimhan-Seshadri theorem in the duality:
- Herbert Clemens, Stuart Raby, Heterotic/F-theory Duality and Narasimhan-Seshadri Equivalence (arxiv:1906.07238)
See also:
-
Michael Douglas, Daniel S. Park, Christian Schnell, The Cremmer-Scherk Mechanism in F-theory Compactifications on K3 Manifolds, JHEP05 (2014) 135 (arXiv:1403.1595)
-
Herbert Clemens, Stuart Raby, Heterotic/F-theory Duality and Narasimhan-Seshadri Equivalence [arXiv:1906.07238]
-
Paul-Konstantin Oehlmann, Fabian Ruehle, Benjamin Sung, The Frozen Phase of Heterotic F-theory Duality [arXiv:2404.02191]
(in relation to D=6 N=(1,0) SCFT)
For both
- Yusuke Kimura, New perspectives in the duality of M-theory, heterotic strings, and F-theory (arXiv:2103.03088)
Last revised on July 18, 2024 at 11:38:42. See the history of this page for a list of all contributions to it.
 (
(