nLab 3d-3d correspondence

Idea

A duality in string theory: relation between the D=3 N=2 SYM worldvolume quantum field theory on M5-brane wrapped on a (hyperbolic) 3-manifold and 3d Chern-Simons theory/analytically continued Chern-Simons theory.

Properties

Relation to volume conjecture

In Gang-Kim-Lee 14b, 3.2, Gang-Kim 18 (21) it is argued that the volume conjecture for Chern-Simons theory on hyperbolic 3-manifolds $\Sigma^3$ is the combined statement of two dualities in string theory

1. AdS/CFT duality

2. 3d-3d correspondence

for the situation of M5-branes wrapped on $\Sigma^3$ (DGKV 10):

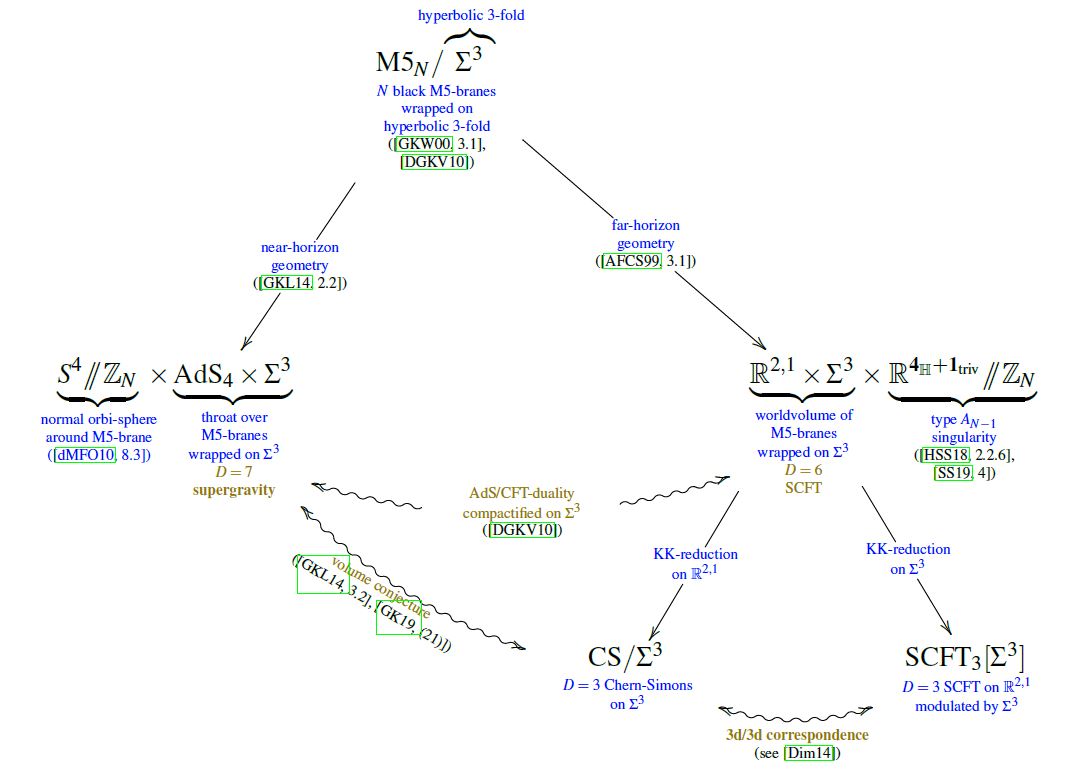
graphics from Sati-Schreiber 19c

Related concepts

Wrapping the M5-brane on a torsion 3-cycle yields: fractional M2-brane.

Wrapping the M5-brane instead on a 2-manifold yields: AGT correspondence.

• McKay correspondence

• AGT correspondence

• knots-quivers correspondence

References

General

Original articles include

• Yuji Terashima, Masahito Yamazaki, $SL(2,\mathbb{R})$ Chern-Simons, Liouville, and Gauge Theory on Duality Walls, JHEP 1108:135, 2011 (arXiv:1103.5748)

• Yuji Terashima, Masahito Yamazaki, Semiclassical Analysis of the 3d/3d Relation, Phys.Rev.D88:026011, 2013 (arXiv:1106.3066)

• Tudor Dimofte, Davide Gaiotto, Sergei Gukov, Gauge Theories Labelled by Three-Manifolds (arXiv:1108.4389)

• Tudor Dimofte, Davide Gaiotto, Sergei Gukov, 3-Manifolds and 3d Indices (arXiv:1112.5179)

• Dongmin Gang, Eunkyung Koh, Sangmin Lee, Jaemo Park, Superconformal Index and 3d-3d Correspondence for Mapping Cylinder/Torus, JHEP01(2014)063 (arXiv:1305.0937)

• Junya Yagi, 3d TQFT from 6d SCFT, JHEP08(2013)017 (arXiv:1305.0291)

• Sungjay Lee, Masahito Yamazaki, 3d Chern-Simons Theory from M5-branes, JHEP1312:035, 2013 (arXiv:1305.2429)

• Clay Cordova, Daniel Jafferis, Complex Chern-Simons from M5-branes on the Squashed Three-Sphere (arXiv:1305.2891)

• Du Pei, Ke Ye, A 3d-3d appetizer, JHEP 11 (2016) 008 (arXiv:1503.04809)

• Sungbong Chun, Sergei Gukov, Sunghyuk Park, Nikita Sopenko, 3d-3d correspondence for mapping tori (arxiv:1911.08456)

• Hee-Joong Chung, Index for a Model of 3d-3d Correspondence for Plumbed 3-Manifolds (arXiv:1912.13486)

Specifically for Seifert 3-manifolds (such as lens spaces):

• Du Pei, 3d-3d correspondence for Seifert manifolds, 2016 (spire:1469350, pdf)

Review is in

• Tudor Dimofte, 3d Superconformal Theories from Three-Manifolds, In: Jörg Teschner (ed.), Exact Results on $\mathcal{N} = 2$ Supersymmetric Gauge Theories, Springer 2015 (arXiv:1412.7129, doi:10.1007/978-3-319-18769-3_11)

Relation of the AGT-correspondence to the D=6 N=(2,0) SCFT and the 3d-3d correspondence:

• Clay Cordova, Daniel Jafferis, Toda Theory From Six Dimensions, J. High Energ. Phys. (2017) 2017: 106 (arxiv:1605.03997)

• Sam van Leuven, Gerben Oling, Generalized Toda Theory from Six Dimensions and the Conifold, J. High Energ. Phys. (2017) 2017: 50 (arxiv:1708.07840)

See also:

• Julius Eckhard, Heeyeon Kim, Sakura Schafer-Nameki, Brian Willett, Higher-Form Symmetries, Bethe Vacua, and the 3d-3d Correspondence (arxiv:1910.14086)

• Yale Fan, 3D-3D Correspondence from Seifert Fibering Operators (arXiv:2008.13202)

Black 5-branes and AdS/CFT

Discussion of D=11 N=1 supergravity solutions for the near horizon geometry of black M5-branes wrapped on hyperbolic 3-manifolds $\Sigma^3 = H^3/\Gamma$:

• Aristomenis Donos, Jerome Gauntlett, Nakwoo Kim, Oscar Varelam, Wrapped M5-branes, consistent truncations and AdS/CMT, JHEP 1012:003, 2010 (arXiv:1009.3805)

• Dongmin Gang, Nakwoo Kim, Sangmin Lee, Holography of Wrapped M5-branes and Chern-Simons theory, Physics Letters B, Volume 733, 2 June 2014, Pages 316-319 (arXiv:1401.3595)

• Dongmin Gang, Nakwoo Kim, Sangmin Lee, Holography of 3d-3d correspondence at Large $N$, JHEP04(2015) 091 (arXiv:1409.6206)

• Dongmin Gang, Nakwoo Kim, Large $N$ twisted partition functions in 3d-3d correspondence and Holography, Phys. Rev. D 99, 021901 (2019) (arXiv:1808.02797)

• Dongmin Gang, Nakwoo Kim, Leopoldo A. Pando Zayas, Precision Microstate Counting for the Entropy of Wrapped M5-branes (arXiv:1905.01559)

Relation to perturbative CS-observables

Relation to perturbative quantization of 3d Chern-Simons theory:

specifically to Reidemeister torsion:

• Dongmin Gang, Seonhwa Kim, Seokbeom Yoon, Adjoint Reidemeister torsions from wrapped M5-branes (arXiv:1911.10718)

Relation to volume conjecture

Discussion of the volume conjecture by combining the 3d/3d correspondence with AdS/CFT in these backgrounds:

• Gang-Kim-Lee 14b, Section 3.2

• Gang-Kim 18, around (21)

Enhanced to a defect field theory:

• Dongmin Gang, Nakwoo Kim, Mauricio Romo, Masahito Yamazaki, Aspects of Defects in 3d-3d Correspondence, J. High Energ. Phys. (2016) (arXiv:1510.05011)

More in:

• Jin-Beom Bae, Dongmin Gang, Jaehoon Lee, 3d $\mathcal{N}=2$ minimal SCFTs from Wrapped M5-branes, JHEP 08 (2017) 118 (arXiv:1610.09259)

Knot invariants

For discussion of knot invariants:

• Sergei Gukov, Pavel Putrov, Cumrun Vafa, Fivebranes and 3-manifold homology, J. High Energ. Phys. (2017) 2017: 71 (arXiv:1602.05302)

Entropy computation

Applied to computation of Bekenstein-Hawking entropy for black holes in string theory:

• Gang-Kim-Pando-Zayas 19

• Francesco Benini, Dongmin Gang, Leopoldo A. Pando Zayas, Rotating Black Hole Entropy from M5 Branes (arXiv:1909.11612)

Anyonic topological order

Arguments realizing anyonic topological order in the worldvolume-field theory on M5-branes via KK-compactification on closed 3-manifolds (Seifert manifolds) analogous to the 3d-3d correspondence (which instead uses hyperbolic 3-manifolds):

• Gil Young Cho, Dongmin Gang, Hee-Cheol Kim: M-theoretic Genesis of Topological Phases, J. High Energ. Phys. 2020 115 (2020) [arXiv:2007.01532, doi:10.1007/JHEP11(2020)115]

• Shawn X. Cui, Paul Gustafson, Yang Qiu, Qing Zhang, From Torus Bundles to Particle-Hole Equivariantization, Lett Math Phys 112 15 (2022) [doi:10.1007/s11005-022-01508-3, arXiv:2106.01959]

• Shawn X. Cui, Yang Qiu, Zhenghan Wang, From Three Dimensional Manifolds to Modular Tensor Categories, Commun. Math. Phys. 397 (2023) 1191–1235 [doi:10.1007/s00220-022-04517-4, arXiv:2101.01674]

• Federico Bonetti, Sakura Schäfer-Nameki, Jingxiang Wu, $MTC[M_3,G]$: 3d Topological Order Labeled by Seifert Manifolds [arXiv:2403.03973]