Schreiber Some thoughts on the future of modal homotopy type theory
A talk that I once gave:
-
Some thoughts on the future of modal homotopy type theory
talk at
Homotopy Type Theory and Univalent Foundations - Mini-Symposium,
within the
German Mathematical Society meeting 2015
21st - 25th Sept 2015, Hamburg
Abstract. In 1991 William Lawvere suggested a) that the future of category theory revolves around toposes equippped with an adjoint system of idempotent (co-)monads (1) and that b) this is formalization of what the ancients had called the “objective logic” (2). While for 1-toposes this seems inconclusive, one finds (3) that internal to ∞-toposes equipped with such adjoint systems much of higher differential geometry and of modern physics has a succinct and useful synthetic formalization. But here the syntax of this internal language is modal homotopy type theory (4). In this talk I survey the immensely rich semantics and the potential prospects of its full syntactic formalization, in the hope to motivate the type theory community to further look into this fascinating but under-explored aspect of their theory.
Contents
Solved problems
Of the three open formalization problems that I had proposed in “Some thoughts…”, two have meanwhile been solved:
Formalization of torsion-free -Structures
Formalization of torsion-free G-structures on geometry of physics – manifolds and orbifolds (the first of the three open problems posed in the talk) was solved in:
-
Formalizing Higher Cartan Geometry in Modal Homotopy Type Theory,
PhD thesis, KIT 2017
(thesis pdf, achived version: web, talk slides: pdf, HoTT-Agda code: DCHoTT-Agda).
A revised and extended version is given in
-
Cartan Geometry in Modal Homotopy Type Theory,
Formalization of the differential hexagon
Formalization of the differential cohomology hexagon in cohesive homotopy type theory has been achieved in:
-
David Jaz Myers, Modal Fracture of Higher Groups, talk at CMU-HoTT Seminar, 2021 (pdf, pdf)
-
David Jaz Myers, Modal Fracture of Higher Groups (arXiv:2106.15390)
Open problems
In continuation of the above, here are further open problems of interest in cohesive modal homotopy type theory.
The overall problem is to establish the running hypothesis: that a progression (this Def.) of adjoint modalities (this Def.) of the form
(cohesion, elasticity, solidity see here) provides a good working foundation for higher differential supergeometry with differential cohomology.
But the problems listed below are meant to be low-hanging concrete problems that should be comparatively straightforward to tackle, while still being of interest. The overall problem will be solved by solving a sufficiently large network of such concrete problems.
Fundamental theorem of calculus (Stokes’ theorem)
Formalization of the fundamental theorem of calculus/Stokes theorem as indicated there remains open.
The same key point as for the differential hexagon (above) needs to be solved.
Bosonic body of supermanifold is manifold
Consider the solid adjoint modalities with Aufhebung and focus on the following fragment of (1)
Here the backslash indicates “Aufhebung to the left” (this Def.), hence that coreduced objects are bosonic:
Problem: Show that if is a formally étale morphism, hence that the naturality square
is an (∞,1)-pullback, then also the bosonic part is formally étale.
(This implies immediately that for a -manifold in the axiomatic sense (here), then is a -manifold, hence that the bosonic body of a supermanifold is an ordinary smooth manifold.)
Here is a classical proof:
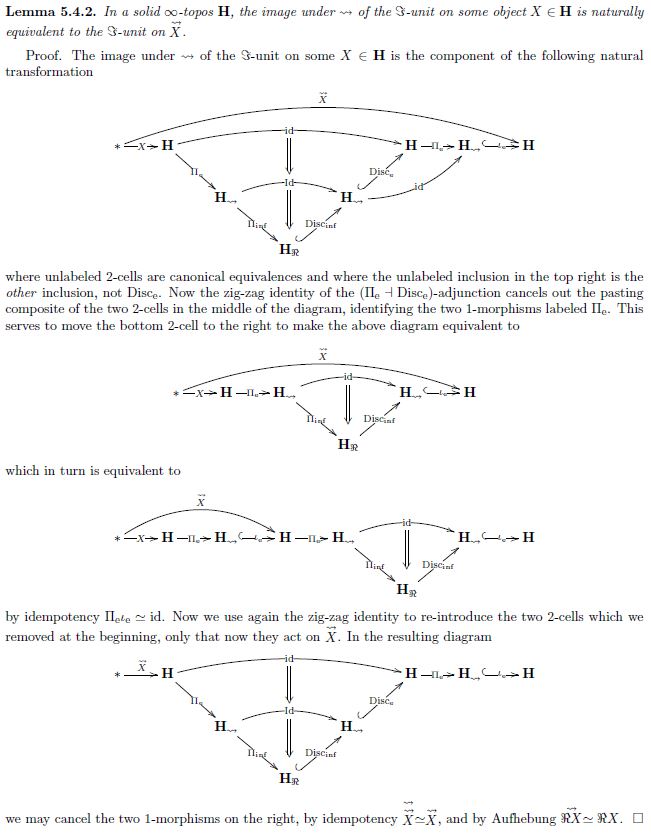
First observe that the image of an -unit on under is naturally equivalent to the -unit of :
With this, the claim follows by applying to the pullback diagram (3) and using that, being a right adjoint, it preserves pullbacks.
Here is a classical proof of (4):
Further directions
The following is a list of subjects that would seem to naturally lend themselves to formalization in cohesive homotopy theory, but where I don’t know yet what exactly a concrete proposition would be that one might aim to prove.
The h-principle in PDE theory
h-principle in partial differential equations (PDE theory)
Focus on the differential cohesion (elasticity) fragment of (1)
Using , one may synthetically speak about partial differential equations, as in
- Igor Khavkine, Urs Schreiber, Synthetic geometry of differential equations (arXiv:1701.06238, v2, talk slides, talk video)
Using also one may then state the h-principle, as discussed here.
Just defining this should be immediate. Maybe there is a theorem here waiting to be proven.
Knot theory
The very idea of equivalence classes of knots (embeddings of smooth manifolds up to smooth isotopy) is one in differential cohesion (“elastic homotopy theory”), combining concepts of differential geometry (embeddings of smooth manifolds) with homotopy (a smooth isotopy between embeddings being a smooth homotopy/path in the smooth space of embeddings).
This should lend itself to formalization in the differential cohesion (elasticity) fragment of (1)
Using the infinitesimal shape modality we may speak about smooth manifolds , as in Wellen 17.
Using in addition the sharp modality we may speak of embedding of smooth manifolds (as discussed here), hence form a homotopy type
of embeddings inside the function type.
Then using the shape modality we obtain . A path in this type is a smooth isotopy. Hence the 0-truncation
should be the type of knots of form inside .
Related talks
Last revised on June 16, 2022 at 08:00:20. See the history of this page for a list of all contributions to it.