nLab F-theory on Spin(7)-manifolds
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
Idea
The KK-compactification of F-theory on Spin(7)-manifolds to 4d. Differs subtly from F-theory on CY4.
Related by T-duality to 3d M-theory on Spin(7)-manifolds
Properties
(Non-)Supersymmetry and (vanishing) cosmological constant
What has been called Witten's dark fantasy in Heckmann-Lawrie-Lin-Zoccarato 19, Section 8 is an argument, going back to Witten 95a, Witten 95b, Sec. 3, Witten 00, p. 7 for the existence of non-perturbative non-supersymmetric 4d string vacua/string phenomenology with fundamentally vanishing cosmological constant (“dark energy”).
The original idea was formulated in terms of 3d M-theory on 8-manifolds decompactified at strong coupling to 4d via duality between M-theory and type IIA string theory (recall the super 2-brane in 4d).
Based on the observation of Vafa 96, Section 4.3 that the argument should have a natural realization in 4d F-theory on Spin(7)-manifolds (T-dual to the previous perspective), a detailed construction was finally laid out in Bonetti-Grimm-Pugh 13, Heckmann-Lawrie-Lin-Zoccarato1 18, Heckman-Lawrie-Lin-Sakstein-Zoccarato 19.
The key technical point is the claim that a careful analysis of D=4 N=1 supergravity obtained after KK-compactification of F-theory on Spin(7)-manifolds T-dual to M-theory on Spin(7)-manifolds reveals a “1/2 supersymmetry” where
-
the vacuum state is supersymmetric and hence has vanishing cosmological constant;
-
but no finite-energy-excitation of the vacuum appears supersymmetrically,
hence fermions and bosons in the model do not appear in supersymmetric spectra.
(Vafa 96, Sec. 4.3 BGP 13, HLLZ 18, Sec. 4)
Relation to J-twisted Cohomotopy
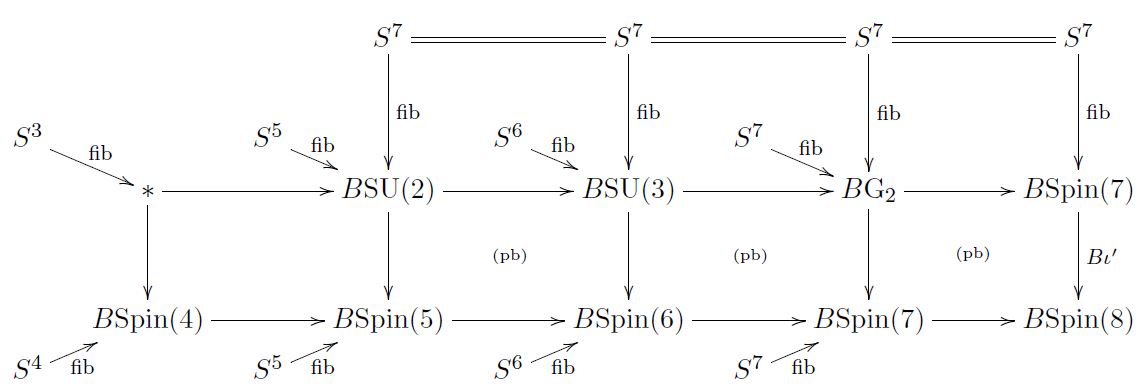
On a spin-manifold of dimension 8 a choice of topological Spin(7)-structure is equivalently a choice of cocycle in J-twisted Cohomotopy cohomology theory. This follows (FSS 19, 3.4) from
-
the standard coset space-structures on the 7-sphere (see here)
-
the fact that coset spaces are the homotopy fibers of the maps of the corresponding classifying spaces (see here)
Related concepts
F-theory KK-compactified on elliptically fibered complex analytic fiber
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| F-theory | F-theory on CY2 | F-theory on CY3 | F-theory on CY4 | F-theory on CY5 |
References
General
The concept goes back to
- Cumrun Vafa, Section 4.3 of: Evidence for F-Theory, Nucl. Phys. B469:403-418, 1996 (arxiv:hep-th/9602022)
See also:
-
Mariana Graña, C. S. Shahbazi, Marco Zambon, -manifolds in compactifications to four dimensions, JHEP11(2014)046 (arXiv:1405.3698)
-
Andreas Braun, Sakura Schafer-Nameki, Spin(7)-Manifolds as Generalized Connected Sums and 3d Theories, JHEP06(2018)103 (arXiv:1803.10755)
(generalization of compact twisted connected sum G₂-manifolds)
Relating M-theory on Spin(7)-manifolds with F-theory on Spin(7)-manifolds via Higgs bundles:
- Mirjam Cvetic, Jonathan Heckman, Thomas B. Rochais, Ethan Torres, Gianluca Zoccarato, Geometric Unification of Higgs Bundle Vacua (arXiv:2003.13682)
Witten’s Dark Fantasy
Already Vafa 96, Section 4.3 mentions the relation to Witten's Dark Fantasy, then developed in
-
Federico Bonetti, Thomas Grimm, Tom Pugh, Non-Supersymmetric F-Theory Compactifications on Manifolds, JHEP 01 (2014) 112 (arXiv:1307.5858)
-
Federico Bonetti, Thomas Grimm, Eran Palti, Tom Pugh, F-Theory on Manifolds: Weak-Coupling Limit, JHEP 02 (2014) 076 (arXiv:1309.2287)
-
Jonathan Heckman, Craig Lawrie, Ling Lin, Gianluca Zoccarato, F-theory and Dark Energy, Fortschritte der Physik (arXiv:1811.01959, doi:10.1002/prop.201900057)
-
Jonathan Heckman, Craig Lawrie, Ling Lin, Jeremy Sakstein, Gianluca Zoccarato, Pixelated Dark Energy (arXiv:1901.10489)
See also
-
Tom Pugh, M-theory on -manifold duals and their F-theory duals (pdf)
-
Federico Bonetti, Thomas Grimm, Eran Palti, Tom Pugh, F-Theory on Spin(7) Manifolds: Weak-Coupling Limit, J. High Energ. Phys. (2014) 2014: 76 (arXiv:1309.2287)
Last revised on July 18, 2024 at 10:56:31. See the history of this page for a list of all contributions to it.