nLab Gauss law
Context
Physics
physics, mathematical physics, philosophy of physics
Surveys, textbooks and lecture notes
theory (physics), model (physics)
experiment, measurement, computable physics
-
-
-
Axiomatizations
-
Tools
-
Structural phenomena
-
Types of quantum field thories
-
Differential cohomology
Ingredients
Connections on bundles
Higher abelian differential cohomology
Higher nonabelian differential cohomology
Fiber integration
Application to gauge theory
Contents
Idea
The Gauss law is, originally, one of the equations of motion of electromagnetism, specifically of its electric field-sector, relating the divergence of the electric field to the electric charge density at each point of space. But the name has come to be commonly used also more generally for the corresponding equation of Yang-Mills theory and also for higher gauge theories, all of which are closely similar equations when formulated via differential forms in exterior calculus.
In the Hamiltonian formulation of these theories, the Gauss law appears as a first class constraint on the canonical phase space whose Hamiltonian vector field is that which generates the gauge transformations.
In form analogous to the Gauss law is a dual statement for the magnetic field, accordingly also known as the magnetic Gauss law and as such also part of Maxwell's equations. However, in traditional Hamiltonian phase space-formulation of electromagnetism, where the magnetic but not the electric field is assumed to have a gauge potential, the symmetry between these two laws is broken (the magnetic Gauss law is not a phase space constraint but a differential Bianchi identity implied by the existence of a gauge potential).
Statement
In electromagnetism
In its original form (named after Gauß 1877), the Gauß law of electromagnetism asserts that the total flux of the electric field through any closed surface (in physical space) is proportional to the total electric charge enclosed by that surface, otherwise irrespective of the charge distribution. In its differential form, the Gauss law is part of what later became Maxwell's equations of electromagnetism.
In terms of modern differential geometry, with
-
denoting the 3-dimensional smooth manifold representing physical space (in this context often but not necessarily assumed to be the Euclidean space ),
-
denoting the differential 2-form which representes the electric field’s flux density
(beware that this 2-form is the spatial Hodge dual of the electric vector field 1-form used elsewhere),
-
denoting an orientable 3-dimensional submanifold with boundary,
-
denoting its boundary, a closed orientable 2-dimensional submanifold,
-
denoting the total electric charge on ,
-
denoting the integral of over , hence the total electric flux through ,
the Gauss law in its original integral form states that the last two quantities are proportional to each other:
with the constant of proportionality depending on conventions but typically being the inverse of the permittivity of the vacuum.
By the Stokes theorem and with
-
denoting a differential 3-form representing the electric charge density, i.e. such that
-
,
-
denoting the de Rham differential of the electric flux density, representing its divergence,
the integral law (1) is equivalent to the following differential form of the Gauss law:
It is in this differential form that the Gauss law is part of the modern form of Maxwell's equations (see their formulation in exterior calculus here).
In Yang-Mills theory
The differential form of the Gauss law (2) generalizes immediately to Yang-Mills theory with gauge Lie algebra by enhancing the de Rham differential to the corresponding covariant differential with respect to the given gauge potential.
(…)
In higher gauge theory
The generalization of Gauss laws to higher gauge theory may transparently be understood, in broad generality, by casting the corresponding higher Maxwell-type equations of motion into “duality-symmetric” form (we follow SS23):
Consider:
-
the spacetime dimension,
-
with Hodge star-operator on differential forms
satisfying (see there)
-
an index set of flux species
(subsuming both electric fluxes and magnetic fluxes, both now allowed of further different species),
-
an indexed set of degrees,
-
an indexed set of flux densities
-
an indexed set of graded-symmetric polynomials in variables,
-
an invertible -matrix
then:
Definition
The corresponding higher Maxwell-type equations on these differential forms/flux densities are, in duality-symmetric form:
-
the system of Bianchi identity differential equations
(3) -
the self-Hodge duality condition
(4)
To extract a Gauss law from such a system of equations, consider the case that the spacetime is globally hyperbolic with associated (by this Prop.) smooth foliation by spacelike Cauchy surfaces exhibited by a diffeomorphism:
This identifies the de Rham differential with the total differential of a double complex of differential forms, bigraded by spatial and by temporal degree:
Denoting by
the kernel of the contraction with the corresponding timelike vector field , every flux density now has a unique decomposition into a summand that has none and a summand that has one factor of :
In terms of these components, the higher Bianchi identities (3) are equivalent to the following system of differential equations:
-
higher Gauss laws
(5) -
higher Faraday-Ampère laws
(6)
Hence in the duality-symmetric formulation of higher gauge theory, the Gauss law is just the spatial component of the Bianchi identity.
Moreover, one finds that the higher Gauss law (5) is a first class constraint in that it is preserved by the time evolution presribed by the higher Faraday-Ampère law (5), so that the solution space of the higher Maxwell equations is identified with the space of flux densities on any Cauchy surface
that satisfy (just) the higher Gauss law:
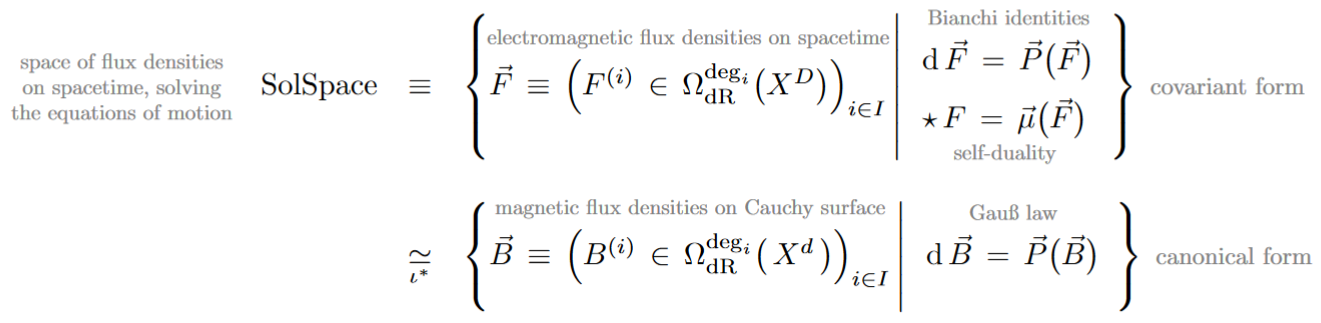
In examples relevant in practice, the functorial assignment of these canonical solution spaces is representable by the formal dual of a dgc-algebra which embodies the Bianchi identities as abstract dg-algebraic relations:
as
This is equivalently the Chevalley-Eilenberg algebra of a characteristic -algebra (by the discussion there), making the right hand side the flat -algebra valued differential forms:
with the higher Gauss law being exactly the flatness condition.
Example
(ordinary Gauss law as special case of higher Gauss law)
The ordinary case (above) of the Gauss law in vacuum electromagnetism (ie. with vanishing electric charge density) is obtained from Def. by setting
-
.
This gives the electric and magnetic Gauss laws as
where self-duality constraint identifies the elctric flux density equivalently as .
Example
(chiral boson in 2d)
(…)
Example
(RR-fields in D=10 supergravity)
(…)
Example
(C-field in D=11 supergravity)
(…)
Related concepts
References
General
Named after:
-
Carl F. Gauß, Theoria attractionis corporum sphaeroidicorum ellipticorum homogeneorum, methodo nova tractata, Commentationes Societatis Regiae Scientiarum Göttingensis Recentiores. Comm. Class. Math. 2 (1813) 1–24 [PPN35283028X_0002_2NS]
reprinted in: Carl Friedrich Gauss – Werke 5, Springer (1877) 2-22 [doi:10.1007/978-3-642-49319-5_1]
For more see any of the references at Maxwell's equations, such as:
- Friedrich W. Hehl, Yuri N. Obukhov, I.1 & B1.45 in: Foundations of Classical Electrodynamics – Charge, Flux, and Metric, Progress in Mathematical Physics 33, Springer (2003) [doi:10.1007/978-1-4612-0051-2]
See also:
- Wikipedia, Gauss’s law
As a phase space constraint
Discussion of the Gauss law as a first-class constraint on phase space:
In Maxwell theory:
-
Daniel N. Blaschke, François Gieres, equation (5.8) in: On the canonical formulation of gauge field theories and Poincaré transformations, Nuclear Physics B 965 (2021) 115366 [doi:10.1016/j.nuclphysb.2021.115366, arXiv:2004.14406]
-
Marc Henneaux, Claudio Teitelboim, p. 456 in: Quantization of Gauge Systems, Princeton University Press 1992 [ISBN:9780691037691, jstor:j.ctv10crg0r]
- John L. Friedman, Nicholas J. Papastamatiou, equation (3.9) in: On the canonical quantization of Yang-Mills theories, Nuclear Physics B 219 1 (1983) 125-142 [doi:10.1016/0550-3213(83)90431-5]
In relation to locality
The Gauss law in relation to non-locality of charged states in quantum field theory:
-
Giovanni Morchio, Franco Strocchi, Localization and symmetries, J. Phys. A 40 (2007) 3173-3188 [arXiv:math-ph/0607015, doi:10.1088/1751-8113/40/12/S17]
-
Detlev Buchholz, Fabio Ciolli, Giuseppe Ruzzi, Ezio Vasselli, Gauss’s law, the manifestations of gauge fields, and their impact on local observables [arXiv:2212.11009]
see also in relation to infraparticles:
- Detlev Buchholz, Gauss’ law and the infraparticle problem, Phys. Lett. B 174 (1986) 331-334 [doi:10.1016/0370-2693(86)91110-X]
Last revised on January 27, 2024 at 15:18:58. See the history of this page for a list of all contributions to it.