nLab Spin(5)/SU(2) is the 7-sphere
Context
Group Theory
- group, ∞-group
- group object, group object in an (∞,1)-category
- abelian group, spectrum
- super abelian group
- group action, ∞-action
- representation, ∞-representation
- progroup
- homogeneous space
Classical groups
Finite groups
Group schemes
Topological groups
Lie groups
Super-Lie groups
Higher groups
Cohomology and Extensions
Related concepts
Geometry
higher geometry / derived geometry
Ingredients
Concepts
-
geometric little (∞,1)-toposes
-
geometric big (∞,1)-toposes
Constructions
Examples
-
derived smooth geometry
Theorems
Contents
Statement
The coset space of Spin(5) by its subgroup SU(2) is diffeomorphic to the standard 7-sphere:
This is however not an isometry to the standard Riemannian manifold-structure (“round n-sphere”), whence one speaks of a squashed n-sphere.
The identification (1) follows via the exceptional isomorphisms
and
as a special case of the general statement
(see this Prop.).
Related concepts
coset space-structures on n-spheres:
| standard: | |
|---|---|
| this Prop. | |
| this Prop. | |
| this Prop. | |
| exceptional: | |
| Spin(7)/G₂ is the 7-sphere | |
| since Spin(6) SU(4) | |
| since Sp(2) is Spin(5) and Sp(1) is SU(2), see Spin(5)/SU(2) is the 7-sphere | |
| G₂/SU(3) is the 6-sphere | |
| Spin(9)/Spin(7) is the 15-sphere |
see also Spin(8)-subgroups and reductions
homotopy fibers of homotopy pullbacks of classifying spaces:
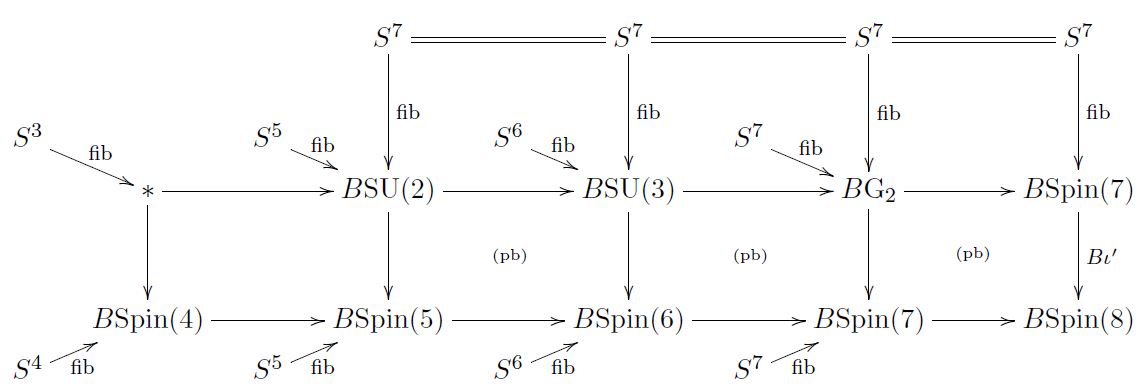
(from FSS 19, 3.4)
References
- Alfred Gray, Paul S. Green, p. 2 of Sphere transitive structures and the triality automorphism, Pacific J. Math. Volume 34, Number 1 (1970), 83-96 (euclid:1102976640)
Discussion of this squashed 7-sphere coset space as a fiber for KK-compactification of 11-dimensional supergravity:
-
M. A. Awada, Mike Duff, Christopher Pope, Supergravity Breaks Down to , Phys. Rev. Lett. 50, 294 – Published 31 January 1983 (doi:10.1103/PhysRevLett.50.294)
-
Mike Duff, Bengt Nilsson, Christopher Pope, Spontaneous Supersymmetry Breaking by the Squashed Seven-Sphere, Phys. Rev. Lett. 50, 2043 – Published 27 June 1983; Erratum Phys. Rev. Lett. 51, 846 (doi:10.1103/PhysRevLett.50.2043)
Last revised on April 29, 2019 at 08:36:47. See the history of this page for a list of all contributions to it.