nLab space attachment
Context
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Contents
Idea
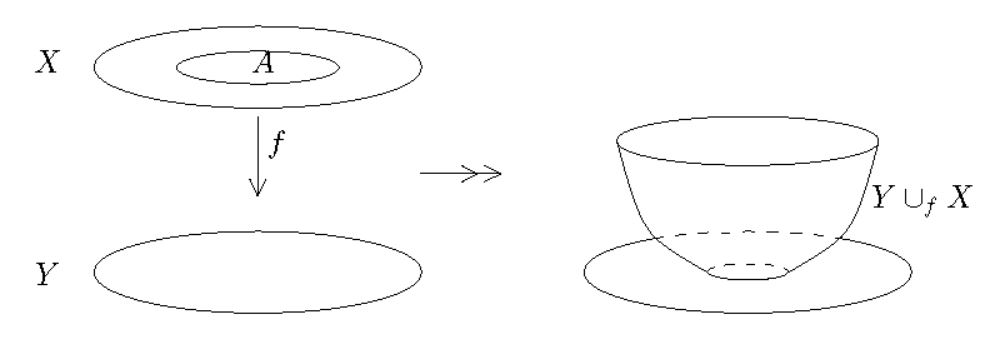
In topology, the result of a space attachment (sometimes called an attaching space or adjunction space) is a topological space, denoted , which is constructed by “attaching” or “gluing” two topological spaces and along a topological subspace by means of a continuous function . The function is then called the attaching map.
(graphics taken from AGP08, §3.1)
More abstractly, space attachments are pushouts along monomorphisms in the category Top of all topological spaces. The formally dual concept is that of fiber spaces or more generally of fiber products of topological spaces.
Definition
Let be topological spaces, let be a topological subspace and let be a continuous function.
Then the attaching space may be realized as the quotient topological space of the disjoint union space by the equivalence relation which identifies a point with its image :
More category theoretically, the attaching space is the pushout in the category Top of topological spaces of the subspace inclusion along , i.e. the topological space which is universal with the property that it makes the following square commute:
For more on this see at Top – Universal constructions.
Examples
- In forming topological cell complexes such as CW-complexes, one consecutively forms space attachments along (n-1)-sphere inclusions as boundaries of n-disks. These are called cell attachments.
Related concepts
examples of universal constructions of topological spaces:
References
-
Marcelo Aguilar, Samuel Gitler, Carlos Prieto, §3.1 in: Algebraic topology from a homotopical viewpoint, Springer (2008) [doi:10.1007/b97586]
-
Raoul Bott, Loring Tu, Chapter 17, p. 217 of: Differential Forms in Algebraic Topology, Graduate Texts in Mathematics 82, Springer (1982) [doi:10.1007/978-1-4757-3951-0]
See also
- Wikipedia, Adjunction space
Last revised on February 11, 2023 at 13:14:20. See the history of this page for a list of all contributions to it.