nLab Urysohn's lemma
Context
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Contents
Idea
Urysohn’s lemma (prop. below) states that on a normal topological space disjoint closed subsets may be separated by continuous functions in the sense that a continuous function exists which takes value 0 on one of the two subsets and value 1 on the other (called an “Urysohn function”, def. ) below. In fact the existence of such functions is equivalent to a space being normal (remark below).
Urysohn’s lemma is a key ingredient for instance in the proof of the Tietze extension theorem and in the proof of the existence of partitions of unity on paracompact topological spaces. See the list of implications below.
Statement
Definition
(Urysohn function)
Let be a topological space, and let be disjoint closed subsets. Then an Urysohn function for this situation is
to the closed interval equipped with its Euclidean metric topology, such that
-
it takes the value 0 on and the value 1 on :
Proposition
(Urysohn’s lemma)
Assuming excluded middle then:
Let be a normal (or ) topological space, and let be two disjoint closed subsets of . Then there exists an Urysohn function (def. ).
Remark
Beware that the function in prop. may take the values 0 or 1 even outside of the two subsets. The condition that the function takes value 0 or 1, respectively, precisely on the two subsets corresponds to perfectly normal spaces.
Remark
It is immediate that, conversely, the existence of an Urysohn function (def. ) implies that the topological space is normal. For let be disjoint closed subsets, and consider a continuous function with and then
are disjoint open neighbourhoods of these subsets.
Hence Urysohn’s lemma shows that a topological space being normal is equivalent to it admitting Urysohn functions.
Proof
Proof
Set
Since by assumption
we have
Notice that (by this lemma) if a space is normal then every open neighbourhood of a closed subset contains a smaller neighbourhood together with its closure
Apply this fact successively to the above situation to obtain the following infinite sequence of nested open subsets and closed subsets
and so on, labeled by the dyadic rational numbers within
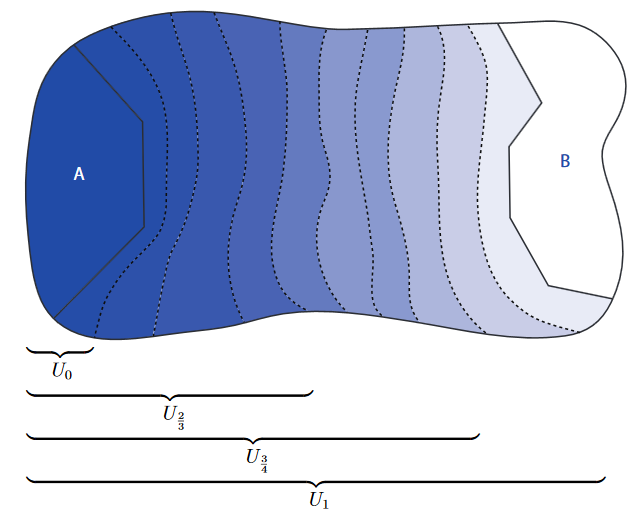
with the property
Define then the function
to assign to a point the infimum of the labels of those open subsets in this sequence that contain :
Here the limit is over the directed set of those that contain , ordered by reverse inclusion.
This function clearly has the property that and . It only remains to see that it is continuous.
To this end, first observe that
Here it is immediate from the definition that and that . For the remaining implication, it is sufficient to observe that
where is the boundary of .
This holds because the dyadic numbers are dense in . (And this would fail if we stopped the above decomposition into -s at some finite .) Namely, in one direction, if then for every small positive real number there exists a dyadic rational number with , and by construction hence . This implies that .
Now we claim that for all then
Thereby and are exhibited as unions of open subsets, and hence they are open.
Regarding the first point:
and
Regarding the second point:
and
(In these derivations we repeatedly use that is dense in , and we use the contrapositions of and , by excluded middle.)
Now since the subsets form a sub-base for the Euclidean metric topology on , it follows that all pre-images of are open, hence that is continuous.
Implications
Urysohn’s lemma is key in the proof of many other theorems, for instance
Related statements
References
Due to Pavel Urysohn.
-
Terence Tao, 245B, Notes 12: Continuous functions on locally compact Hausdorff spaces
-
Wikipedia, Urysohn’s lemma
Lectures notes include
- Tarun Chitra, section 2.1 of The Stone-Cech Compactification 2009 pdf
Last revised on December 6, 2018 at 21:35:08. See the history of this page for a list of all contributions to it.