nLab space attachment

Idea

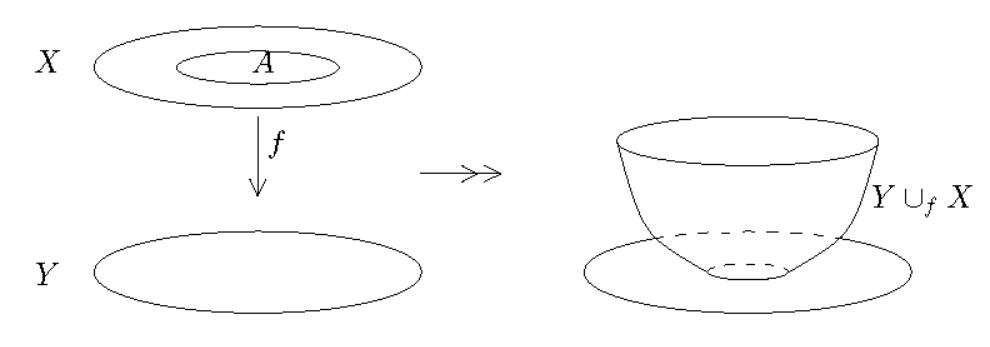
In topology, the result of a space attachment (sometimes called an attaching space or adjunction space) is a topological space, denoted $X \cup_{f} Y$, which is constructed by “attaching” or “gluing” two topological spaces $X$ and $Y$ along a topological subspace $A \subset X$ by means of a continuous function $f \colon A \to Y$. The function $f$ is then called the attaching map.

More abstractly, space attachments are pushouts along monomorphisms in the category Top of all topological spaces. The formally dual concept is that of fiber spaces or more generally of fiber products of topological spaces.

Definition

Let $X,Y \in Top$ be topological spaces, let $A \subset X$ be a topological subspace and let $f \colon A \to Y$ be a continuous function.

Then the attaching space $X \cup_f Y \in Top$ may be realized as the quotient topological space of the disjoint union space $X \sqcup Y$ by the equivalence relation which identifies a point $x \in A \subset X$ with its image $f(x) \in Y$:

$$X \cup_f Y \;\simeq\; \left( X \sqcup Y \right)/\sim \,.$$

More category theoretically, the attaching space is the pushout in the category Top of topological spaces of the subspace inclusion $i \colon A \hookrightarrow X$ along $f$, i.e. the topological space which is universal with the property that it makes the following square commute:

$$\array{ A &\overset{\phantom{A}i\phantom{A}}{\hookrightarrow}& X \\ {}^{\mathllap{f}}\downarrow &(po)& \downarrow \\ Y &\longrightarrow& X \cup_f Y } \,.$$

For more on this see at Top – Universal constructions.

Examples

• In forming topological cell complexes such as CW-complexes, one consecutively forms space attachments along (n-1)-sphere inclusions as boundaries of n-disks. These are called cell attachments.

Related concepts

examples of universal constructions of topological spaces:

$\phantom{AAAA}$limits	$\phantom{AAAA}$colimits
$\,$ point space$\,$	$\,$ empty space $\,$
$\,$ product topological space $\,$	$\,$ disjoint union topological space $\,$
$\,$ topological subspace $\,$	$\,$ quotient topological space $\,$
$\,$ fiber space $\,$	$\,$ space attachment $\,$
$\,$ mapping cocylinder, mapping cocone $\,$	$\,$ mapping cylinder, mapping cone, mapping telescope $\,$
	$\,$ cell complex, CW-complex $\,$

• Whitehead product

References

• Raoul Bott, Loring Tu, Chapter 17, p. 217 of Differential Forms in Algebraic Topology, Graduate Texts in Mathematics 82, Springer 1982 (doi:10.1007/BFb0063500)

See also

• Wikipedia, Adjunction space