nLab simple Lie group
Context
-Lie theory
∞-Lie theory (higher geometry)
Background
Smooth structure
Higher groupoids
Lie theory
∞-Lie groupoids
∞-Lie algebroids
Formal Lie groupoids
Cohomology
Homotopy
Related topics
Examples
-Lie groupoids
-Lie groups
-Lie algebroids
-Lie algebras
Simple Lie groups
Definition
A simple Lie group is a non-abelian connected Lie group with no nontrivial connected normal subgroups.
Via Lie's theorems this is equivalent to the Lie algebra of being a simple Lie algebra (over the real numbers).
Remark
This is not the same thing as a simple object in LieGrp (or even in ). However, the Lie algebra associated to a simple Lie group is always a simple Lie algebra (although that definition also requires a non-abelian clause).
Classification
The classification of simple Lie groups consists of four infinite series – the classical Lie groups – and five separate cases – the exceptional Lie groups.
See Wikipedia's list of simple Lie groups.
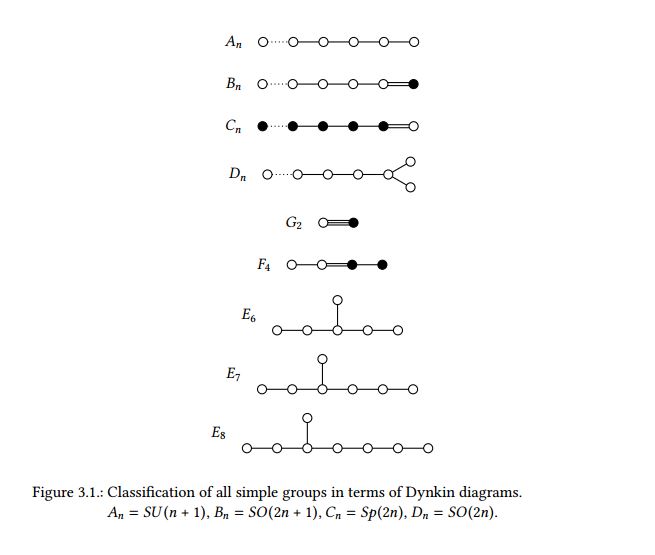
graphics grabbed from Schwichtenberg
See also at ADE classification
Examples
-
The special unitary group is simple for all .
-
The special orthogonal group is simple at least for (corresponding to SO(8)), hence so are the corresponding spin groups.
References
- Notes on simple Lie algebras and Lie groups (pdf)
See also
- Wikipedia, Simple Lie group
Last revised on August 29, 2019 at 08:00:02. See the history of this page for a list of all contributions to it.