nLab flop transition

Idea

The flop transition is a continuous path in a space of noncommutative 2-geometries that starts at an ordinary complex 3-dimensional Calabi-Yau space, then passes through a point that does not correspond to an ordinary geometry (the Gepner point) and emerges afterwards again as an ordinary CY-geometry – but now with different topology.

This was found and discussed in the context of string theory but the phenomenon is a general abstract one in the theory of 2d SCFTs regarded as generalized geometries – as described at 2-spectral triple.

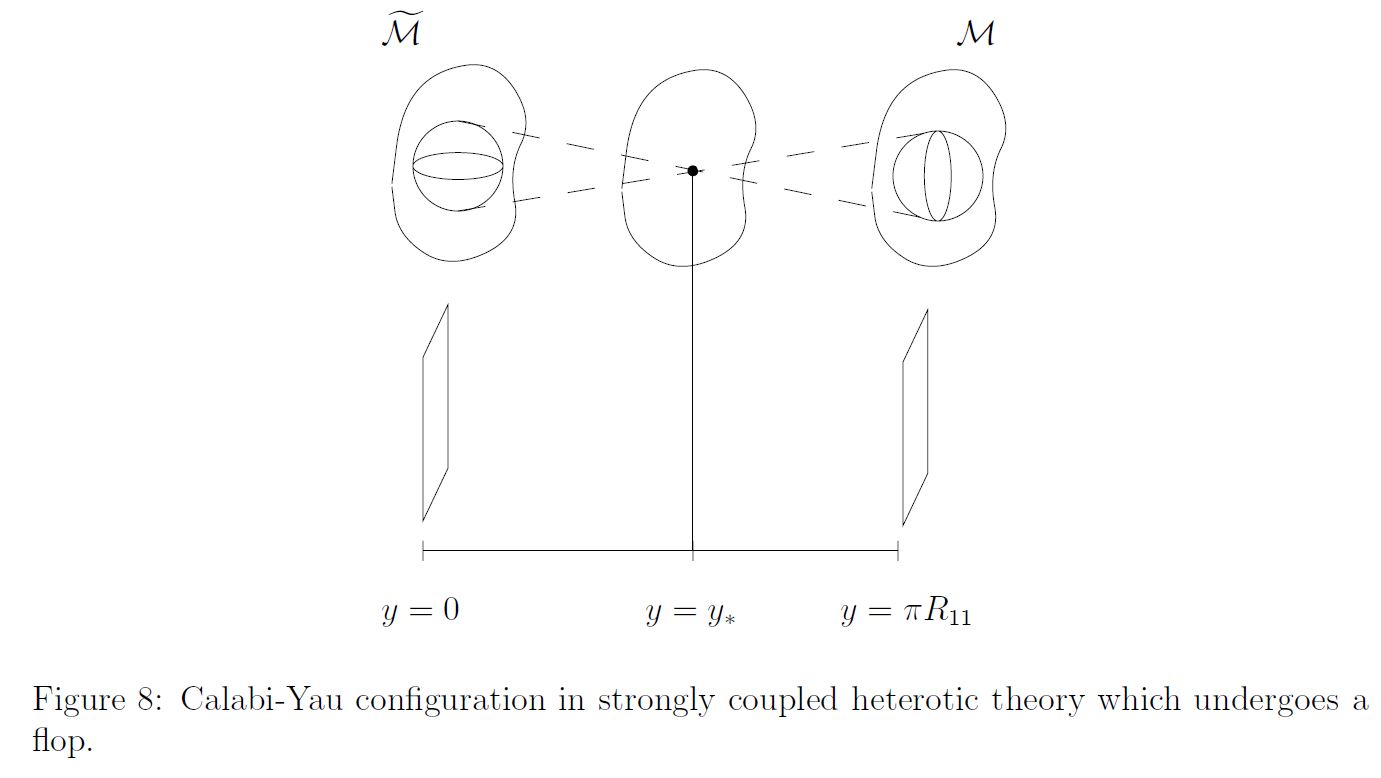
graphics grabbed from Greene 00

Related concepts

• conifold tansition

• moduli space of Calabi-Yau spaces

References

A survey is in

• Brian Greene, String Theory on Calabi-Yau Manifolds (arXiv:hep-th/9702155)

A rough and brief survey of the flop transition and related phenomena with many pointers to original literature is also given in

• Brian Greene, Aspects of collapsing cocycles, in Proceedings of Strings 2000, WorldScientific 2001 (pdf, doi:10.1142/4599)

See also

• Shing-Tung Yau, Moduli of high dimensional Calabi-Yau manifolds

On the quantum volume? of vanishing cycles in the flop transition:

• Brian Greene, Yakov Kanter, Small Volumes in Compactified String Theory, Nucl.Phys.B497:127-145,1997 (arXiv:hep-th/9612181)

• Brian Greene, Calin Lazaroiu, Collapsing D-Branes in Calabi-Yau Moduli Space: I, Nucl.Phys. B604 (2001) 181-255 (arXiv:hep-th/0001025)

• Calin Lazaroiu, Collapsing D-branes in one-parameter models and small/large radius duality, Nucl.Phys. B605 (2001) 159-191 (arXiv:hep-th/0002004)

• Mark Raugas, D-Branes and Vanishing Cycles in Higher Dimensions (arXiv:hep-th/0102133)