nLab magnetic field
Context
Physics
physics, mathematical physics, philosophy of physics
Surveys, textbooks and lecture notes
theory (physics), model (physics)
experiment, measurement, computable physics
-
-
-
Axiomatizations
-
Tools
-
Structural phenomena
-
Types of quantum field thories
-
Contents
Idea
In physics the electromagnetic field may be decomposed, over a choice of coordinate chart of spacetime, into two components: the electric field and the magnetic field.
See there there for more.
Properties
Magnetic flux quantization in type II superconductors
Due to the Meissner-Ochsenfeld effect, a superconductor placed in a sufficiently small external magnetic field (aligned along some axis) “expels” that field , making the total magnetic field in the bulk of the superconductor vanish. However, as the ambient magnetic field exceeds a critical value , this behaviour changes:
-
for type I superconductors, the superconducting state simply breaks down as and the ambient magnetic field fully penetrates the material as for any normal conductor;
-
for type II superconductors the superconducting state eventually also breaks down as , but there is an intermediate parameter region where both regimes mix:
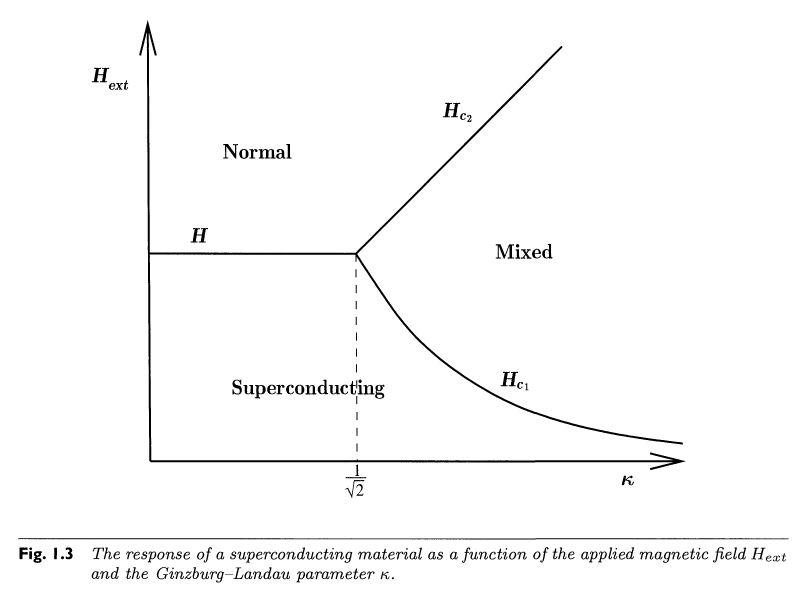
In this mixed regime, a finite number of elementary units of magnetic flux enter the superconductor, carried by little flux tubes inside vortices of electric currents: vortex strings (about a micron in diameter, e.g. Chapman 00, p. 559). Each vortex core carries one unit of magnetic flux – also called a fluxon – while at some small finite distance away from all vortices, the bulk magnetic flux in the superconductor still vanishes (mathematically: it vanishes at infinity, cf. eg. Chapman 2009 (2.31), Timm 2020 (6.101)) :
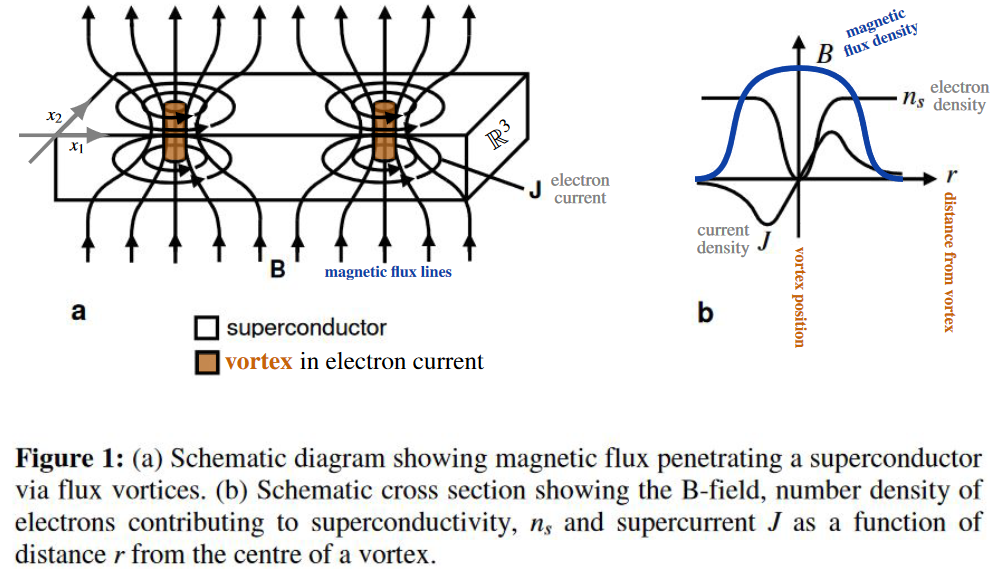
At sufficiently large density these vortices arrange into hexagonal patterns, first described by Abrikosov 57, whence also known as Abrikosov vortices.

This flux quantization in type II superconductors is traditionally explained via the effective field theory provided by the Landau-Ginzburg model; the derivation may be found reviewed in Chapman 00 (Section 2, culminating in (2.33)).
But, as indicated a little more explicitly in Alvarez-Gaumé 98 (Section IV.B, culminating below IV.11), the flux quantization as such is mathematically a direct consequence of the global topological nature of the electromagnetic field, the argument being the direct 2-dimensional analog of the quantization of instantons in QCD in 4d (see also at SU(2)-Instantons – From the correct maths to the traditional physics story) and in fact is but a slight variation of the argument for Dirac charge quantization of magnetic monopoles:
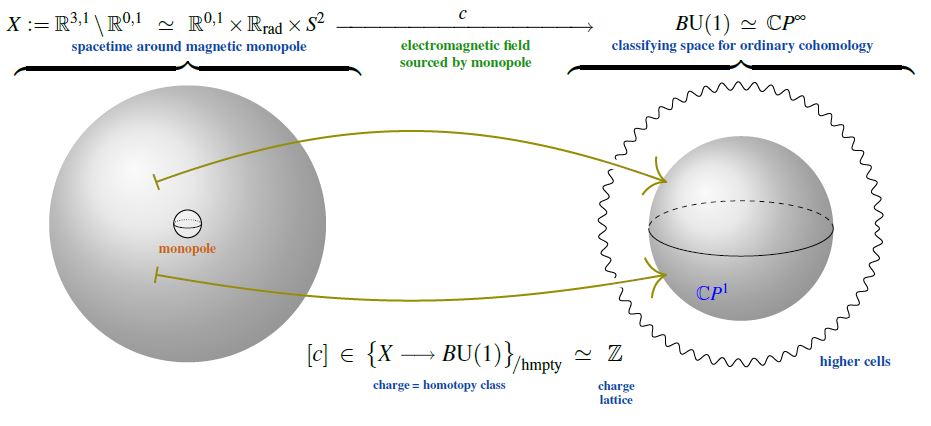
Namely, the electromagnetic field is a connection on a circle bundle, and hence the cohomology classifying space for the topological class of the electromagnetic field is the classifying space of the circle group, which, being an Eilenberg-MacLane space , has second homotopy group the integers:
This implies that on every spacetime which looks, up to homotopy equivalence, like a 2-sphere to the electromagnetic field, the magnetic flux is identified with an element in the group of integers, hence is quantized in integral multiples of some unit flux.
For the case of a (hypothetical) magnetic monopole (e.g. a magnetically charged black hole), it is the spacetime around the monopole (the complement of its worldline in the ambient (asymtptotically) Minkowski spacetime ) which has the homotopy type of a 2-sphere ; this implies the Dirac charge quantization of the magnetic monopole‘s magnetic charge:
For the case of the type II superconductor it is instead the transversal vanishing at infinity of the magnetic field (i.e. the Meissner-Ochsenfeld effect away from the vortices) which implies that the classifying map of the electromagnetic field sees not the full transversal Euclidean plane but its one-point compactification , which introduces an effective 2-sphere topology onto spacetime (same as the 3-sphere in the discussion of Skyrmions and the 4-sphere in the discussion of instantons): . This implies the superconductor’s magnetic flux quantization:
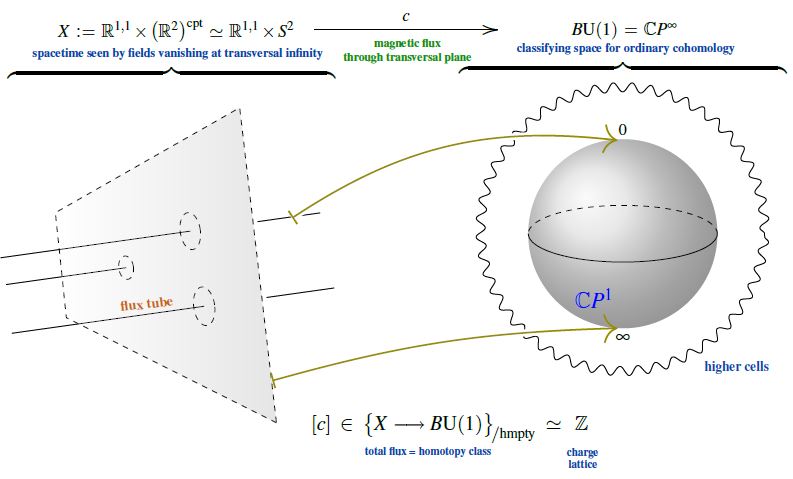
The argument that is given in most references, via consideration of the period of the vector potential on a large circle around the superconductor (e.g. Timm 20, Section 5.3), is secretly just the analysis of this picture through the clutching construction (the direct 2d analog of the discussion at SU(2)-Instantons – From the correct maths to the traditional physics story).
Related oncepts
References
General
See also:
- Wikipedia, Magnetic field
In holographic QCD:
- Umut Gursoy: Holographic QCD and magnetic fields [arXiv:2104.02839]
Motion in magnetic fields
- Dam Thanh Son, Mikhail Stephanov: Relativistic Guiding-Center Motion: Action Principle, Kinetic Theory, and Hydrodynamics, Phys. Rev. Lett. 133 (2024) 145201 [arXiv:2405.08073, doi:10.1103/PhysRevLett.133.145201]
Review:
- Dam Thanh Son: Lorentz-covariant description of relativistic guiding-center motion, talk at Simons Center Physics Seminar (2025-02-12) [recording:scgp:6931]
Last revised on February 14, 2025 at 08:54:49. See the history of this page for a list of all contributions to it.