nLab superconductivity
Context
Solid state physics
-
basics
-
Examples
Contents
Idea
In physics, a superconductor is a conductor whose electrical resistance essentially vanishes below a critical temperature.
At the same time, in their superconducting phase, magnetic fields are expelled from Type I superconductors, while for Type II superconductors there is a second, higher, critical temperature below which the magnetic field may penetrate in integer multiples of unit flux concentrated at a discrete set of points (where the electron-current forms Abrikosov vortices).
Properties
Magnetic flux quantization in type II superconductors
Due to the Meissner-Ochsenfeld effect, a superconductor placed in a sufficiently small external magnetic field (aligned along some axis) “expels” that field , making the total magnetic field in the bulk of the superconductor vanish. However, as the ambient magnetic field exceeds a critical value , this behaviour changes:
-
for type I superconductors, the superconducting state simply breaks down as and the ambient magnetic field fully penetrates the material as for any normal conductor;
-
for type II superconductors the superconducting state eventually also breaks down as , but there is an intermediate parameter region where both regimes mix:
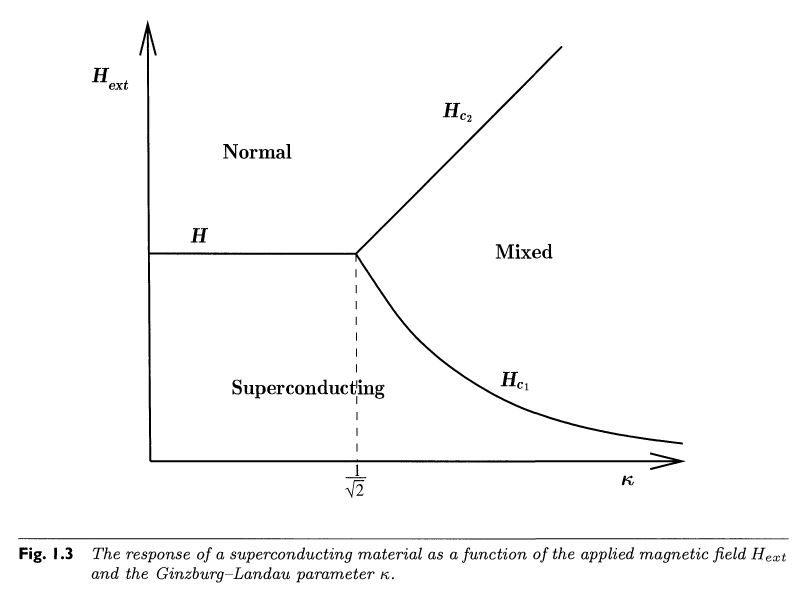
In this mixed regime, a finite number of elementary units of magnetic flux enter the superconductor, carried by little flux tubes inside vortices of electric currents: vortex strings (about a micron in diameter, e.g. Chapman 00, p. 559). Each vortex core carries one unit of magnetic flux – also called a fluxon – while at some small finite distance away from all vortices, the bulk magnetic flux in the superconductor still vanishes (mathematically: it vanishes at infinity, cf. eg. Chapman 2009 (2.31), Timm 2020 (6.101)) :
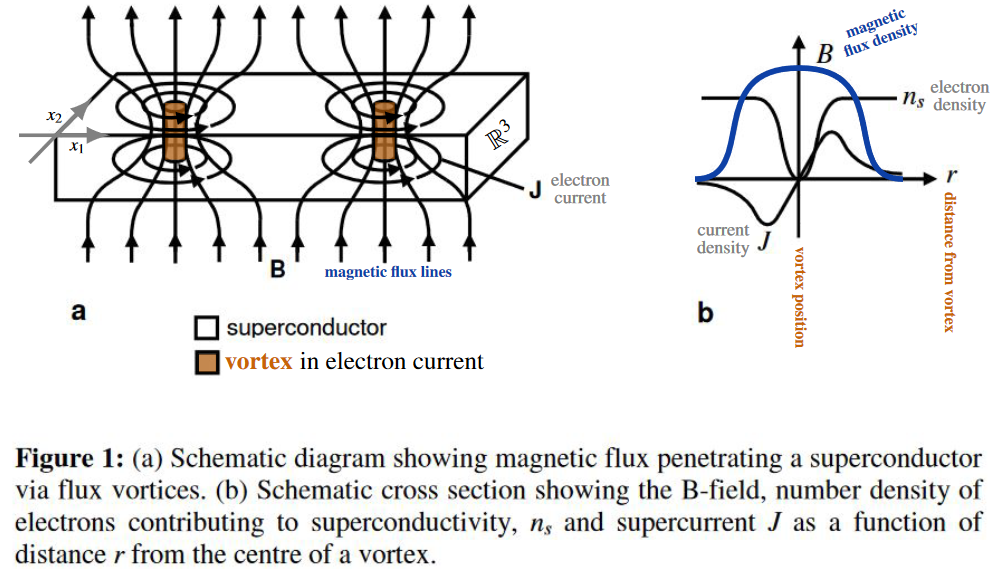
At sufficiently large density these vortices arrange into hexagonal patterns, first described by Abrikosov 57, whence also known as Abrikosov vortices.

This flux quantization in type II superconductors is traditionally explained via the effective field theory provided by the Landau-Ginzburg model; the derivation may be found reviewed in Chapman 00 (Section 2, culminating in (2.33)).
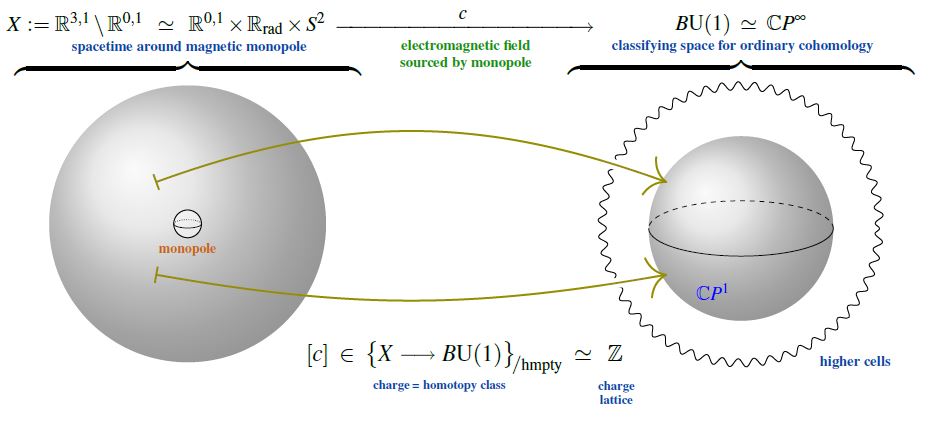
But, as indicated a little more explicitly in Alvarez-Gaumé 98 (Section IV.B, culminating below IV.11), the flux quantization as such is mathematically a direct consequence of the global topological nature of the electromagnetic field, the argument being the direct 2-dimensional analog of the quantization of instantons in QCD in 4d (see also at SU(2)-Instantons – From the correct maths to the traditional physics story) and in fact is but a slight variation of the argument for Dirac charge quantization of magnetic monopoles:
Namely, the electromagnetic field is a connection on a circle bundle, and hence the cohomology classifying space for the topological class of the electromagnetic field is the classifying space of the circle group, which, being an Eilenberg-MacLane space , has second homotopy group the integers:
This implies that on every spacetime which looks, up to homotopy equivalence, like a 2-sphere to the electromagnetic field, the magnetic flux is identified with an element in the group of integers, hence is quantized in integral multiples of some unit flux.
For the case of a (hypothetical) magnetic monopole (e.g. a magnetically charged black hole), it is the spacetime around the monopole (the complement of its worldline in the ambient (asymtptotically) Minkowski spacetime ) which has the homotopy type of a 2-sphere ; this implies the Dirac charge quantization of the magnetic monopole‘s magnetic charge:
For the case of the type II superconductor it is instead the transversal vanishing at infinity of the magnetic field (i.e. the Meissner-Ochsenfeld effect away from the vortices) which implies that the classifying map of the electromagnetic field sees not the full transversal Euclidean plane but its one-point compactification , which introduces an effective 2-sphere topology onto spacetime (same as the 3-sphere in the discussion of Skyrmions and the 4-sphere in the discussion of instantons): . This implies the superconductor’s magnetic flux quantization:
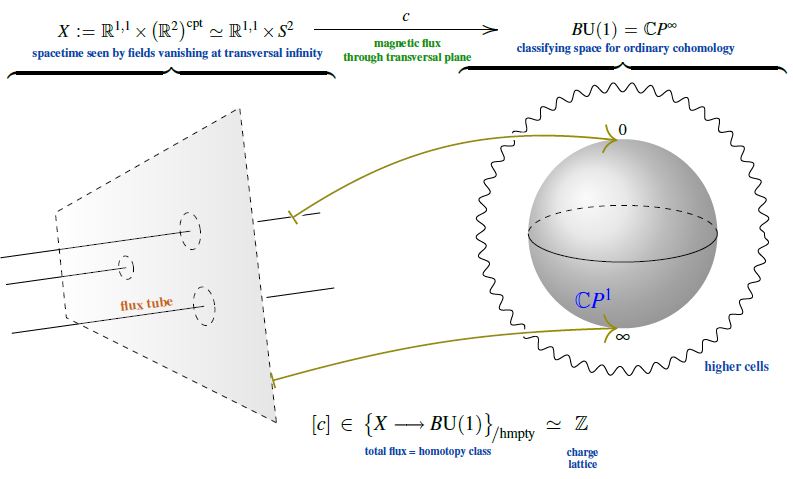
The argument that is given in most references, via consideration of the period of the vector potential on a large circle around the superconductor (e.g. Timm 20, Section 5.3), is secretly just the analysis of this picture through the clutching construction (the direct 2d analog of the discussion at SU(2)-Instantons – From the correct maths to the traditional physics story).
Related concepts
References
General
Comprehensive survey:
Theoretical introduction and review:
-
Lev Landau, Evgeny Lifshitz, Section VI of: Electrodynamics of Continuous Media, volume 8 of: Course of Theoretical Physics, Pergamon Press (1960, 1984) [ISBN:9780750626347, archive, pdf]
-
Alexander L. Fetter, John Dirk Walecka, Ch. 13 of: Quantum theory of many-particle systems, Mcgraw-Hill (1991); Dover (2003) [archive.org]
-
S. J. Chapman, A Hierarchy of Models for Type-II Superconductors, IAM Review Vol. 42, No. 4 (2000), pp. 555-598 (jstor:2653134)
-
Carsten Timm, Theory of Superconductivity, lecture notes (2020-2023) [pdf, pdf]
- Eduardo C. Marino: Quantum Field Theory Approach to Superconductivity, chapter 23 in: Quantum Field Theory Approach to Condensed Matter Physics, Cambridge University Press (2017) [doi:10.1017/9781139696548]
See also:
-
Wikipedia, Superconductivity
-
Wikipedia, Meissner effect
Textbook account in the context of quantum materials and topological insulators:
- Tudor D. Stanescu, Section II.5 of: Introduction to Topological Quantum Matter & Quantum Computation, CRC Press 2020 (ISBN:9780367574116)
Introducing Landau-Ginzburg models in superconductivity:
- Vitaly Ginzburg, Lev Landau, On the Theory of Superconductivity, reprinted In: On Superconductivity and Superfluidity Springer (2009) (doi:1007/978-3-540-68008-6_4)
Introducing the dimer model:
- Daniel S. Rokhsar and Steven A. Kivelson, Superconductivity and the Quantum Hard-Core Dimer Gas, Phys. Rev. Lett. 61, 2376 – Published 14 November 1988 (arXiv:10.1103/PhysRevLett.61.2376)
Argument that superconductors are actually topologically ordered phases of matter:
- Thors Hans Hansson, Vadim Oganesyan, S. L. Sondhi, Superconductors are topologically ordered, Annals Of Physics 313 497 (2004) [arXiv:cond-mat/0404327, doi:10.1016/j.aop.2004.05.006]
On doping semiconductors into superconductors:
- E. Bustarret: Superconductivity in doped semiconductors, Physica C: Superconductivity and its Applications 514 (2015) 36-45 [doi:10.1016/j.physc.2015.02.021]
Vortices and flux quantization
Original articles:
-
Alexei Abrikosov, On the Magnetic properties of superconductors of the second group, Sov. Phys. JETP 5 (1957) 1174-1182; Zh. Eksp. Teor. Fiz. 32 (1957) 1442-1452 [spire:9138, pdf]
-
Alexei Abrikosov, The magnetic properties of superconducting alloys, Journal of Physics and Chemistry of Solids Volume 2, Issue 3, 1957, Pages 199-208 (doi:10.1016/0022-3697(57)90083-5)
Further discussion:
-
A. M. Campbell, Maxwell’s Equations in Superconductors, IEEE Transactions on Applied Superconductivity 17 2 (2007) [doi:10.1109/TASC.2007.900042]
-
Aron J. Beekman, Jan Zaanen, Electrodynamics of Abrikosov vortices: the field theoretical formulation, Front. Phys. 6 (2011) 357–369 [doi:10.1007/s11467-011-0205-0]
Lecture notes:
-
Xiongjie Yu, Vortices in Type-II Superconductors, essay for Emergent States of Matter, Urbana-Champaign (2012) [pdf, pdf]
See also
- Wikipedia, Abrikosov vortex
First experimental detection of flux quantization in superconductors:
-
Bascom S. Deaver, Jr., William M. Fairbank, Experimental Evidence for Quantized Flux in Superconducting Cylinders, Phys. Rev. Lett. 7, 43 – Published 15 (1961) (doi:10.1103/PhysRevLett.7.43)
-
R. Doll, M. Näbauer, Experimental Proof of Magnetic Flux Quantization in a Superconducting Ring, Phys. Rev. Lett. 7, 51 (1961) (doi:10.1103/PhysRevLett.7.51)
More on the experimental detection magnetic flux quantization and vortices:
- J. C. Loudon, P. A. Midgley, Imaging Flux Vortices in Type II Superconductors with a Commercial Transmission Electron Microscope, Ultramicroscopy 109 6 (2009) 700-729 [arXiv:0807.2401, doi:10.1016/j.ultramic.2009.01.008]
More theoretically flavored discussion of the flux quantization mechanism:
- Luis Alvarez-Gaumé, Frederic Zamora, Section IV.B of: Duality in Quantum Field Theory (and String Theory), AIP Conference Proceedings 423, 46 (1998) (arXiv:hep-th/9709180)
On the vortex flux tubes as dynamical vortex strings:
-
Holger Bech Nielsen, Poul Olesen, Vortex-line models for dual strings, Nuclear Physics B Volume 61, 24 September 1973, Pages 45-61 (doi:10.1016/0550-3213(73)90350-7)
-
David Tong, Quantum Vortex Strings: A Review, Annals Phys. 324:30-52, 2009 (arXiv:0809.5060)
On superfluidity/superconductivity of anyons:
- Yi-Hong Chen, Frank Wilczek, Edward Witten, Bertrand Halperin, On Anyon Superconductivity, International Journal of Modern Physics B 03 07 (1989) 1001-1067 (reprinted in Wilczek 1990) doi:10.1142/S0217979289000725, pdf
Superconducting qbits
On realizing qbits and quantum gates (hence quantum computation) via quantum states of magnetic flux through (Josephson junctions in) superconductors, manipulated via electromagnetic pulses:
-
Michel H. Devoret, A. Wallraff, J. M. Martinis, Superconducting Qubits: A Short Review [arXiv:cond-mat/0411174]
-
John Clarke, Frank K. Wilhelm, Superconducting quantum bits, Nature 453 (2008) 1031–1042 doi:10.1038/nature07128
-
Jerry Moy Chow, Quantum Information Processing with Superconducting Qubits (2010) pdf
-
Michel H. Devoret, R. J. Schoelkopf, Superconducting Circuits for Quantum Information: An Outlook, Science 339 6124 (2013) 1169-1174 [doi:10.1126/science.1231930]
-
Jay M. Gambetta, Jerry M. Chow, Matthias Steffen, Building logical qubits in a superconducting quantum computing system, npj Quantum Information 3 2 (2017) doi:10.1038/s41534-016-0004-0
-
Morten Kjaergaard et al. Superconducting Qubits: Current State of Play, Annual Review of Condensed Matter Physics 11 (2019) 369-395 doi:10.1146/annurev-conmatphys-031119-050605
-
He-Liang Huang, Dachao Wu, Daojin Fan, Xiaobo Zhu, Superconducting Quantum Computing: A Review, Science China Information Sciences 63 8 (2020) 1-32 arXiv:2006.10433, doi:10.1007/s11432-020-2881-9
-
S. Kwon et al., Gate-based superconducting quantum computing, Journal of Applied Physics 129 (2021) 041102 doi:10.1063/5.0029735
-
Olivier Ezratty, Perspective on superconducting qubit quantum computing, Eur. Phys. J. A 59 94 (2023) [doi:10.1140/epja/s10050-023-01006-7]
Monograph:
- Chen, Church, Englert, Henkel, Rohwedder, Scully, Zubairy, section 9 of: Quantum Computing Devices Principles, Designs, and Analysis, Routledge (2007) [ISBN:9780367390372]
Fine detail of the pulse control:
-
M. Werninghaus, D. J. Egger, F. Roy, S. Machnes, F. K. Wilhelm, S. Filipp: Leakage reduction in fast superconducting qubit gates via optimal control, npj Quantum Information 7 14 (2021) doi:10.1038/s41534-020-00346-2
-
M. Carroll, S. Rosenblatt, P. Jurcevic, I. Lauer & A. Kandala. Dynamics of superconducting qubit relaxation times, npj Quantum Information 8 132 (2022) doi:10.1038/s41534-022-00643-y
-
Elisha Siddiqui Matekole, Yao-Lung L. Fang, Meifeng Lin, Methods and Results for Quantum Optimal Pulse Control on Superconducting Qubit Systems, 2022 IEEE International Parallel and Distributed Processing Symposium Workshops (2022) arXiv:2202.03260, doi:10.1109/IPDPSW55747.2022.00102
Corrections due to quasiparticle-excitations:
- Leonid I. Glazman, Gianluigi Catelani, Bogoliubov Quasiparticles in Superconducting Qubits, SciPost Phys. Lect. Notes 31 (2021) [arXiv:2003.04366, doi:10.21468/SciPostPhysLectNotes.31]
Anyons in topological superconductors
On anyon-excitations in topological superconductors.
via Majorana zero modes:
Original proposal:
- Nicholas Read, Dmitry Green, Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries, and the fractional quantum Hall effect, Phys. Rev. B61:10267, 2000 (arXiv:cond-mat/9906453)
Review:
-
Sankar Das Sarma, Michael Freedman, Chetan Nayak, Majorana Zero Modes and Topological Quantum Computation, npj Quantum Information 1, 15001 (2015) (nature:npjqi20151)
-
Nur R. Ayukaryana, Mohammad H. Fauzi, Eddwi H. Hasdeo, The quest and hope of Majorana zero modes in topological superconductor for fault-tolerant quantum computing: an introductory overview (arXiv:2009.07764)
-
Yusuke Masaki, Takeshi Mizushima, Muneto Nitta, Non-Abelian Anyons and Non-Abelian Vortices in Topological Superconductors [arXiv:2301.11614]
Further developments:
-
Meng Cheng, Victor Galitski, Sankar Das Sarma, Non-adiabatic Effects in the Braiding of Non-Abelian Anyons in Topological Superconductors, Phys. Rev. B 84, 104529 (2011) (arXiv:1106.2549)
-
Javad Shabani et al., Two-dimensional epitaxial superconductor-semiconductor heterostructures: A platform for topological superconducting networks, Phys. Rev. B 93 155402 (2016) [doi:10.1103/PhysRevB.93.155402, arXiv:1511.01127]
-
Javad Shabani et al., Zero-Energy Modes from Coalescing Andreev States in a Two-Dimensional Semiconductor-Superconductor Hybrid Platform, Phys. Rev. Lett. 119 (2017) 176805 [doi:10.1103/PhysRevLett.119.176805, arXiv:1703.03699]
-
Javad Shabani et al., Fusion of Majorana Bound States with Mini-Gate Control in Two-Dimensional Systems, Nature Communications 13 (2022) 1738-1747 [doi:10.1038/s41467-022-29463-6, arXiv:2101.09272]
-
Javad Shabani et al., Quasiparticle dynamics in epitaxial Al-InAs planar Josephson junctions, PRX Quantum 4 030339 (2023) [doi:10.1103/PRXQuantum.4.030339, arXiv:2303.04784]
-
William F. Schiela, Peng Yu, Javad Shabani: Progress in superconductor-semiconductor topological Josephson junctions, PRX Quantum 5 (2024) 030102 [doi:10.1103/PRXQuantum.5.030102, arXiv:2408.12749]
via Majorana zero modes restricted to edges of topological insulators:
- Biao Lian, Xiao-Qi Sun, Abolhassan Vaezi, Xiao-Liang Qi, Shou-Cheng Zhang: Topological quantum computation based on chiral Majorana fermions, PNA 115 43 (2018) 10938-10942 [doi:10.1073/pnas.1810003115]
Concerning measurement-based quantum gates on Majorana zero modes:
- Torsten Karzig, Yuval Oreg, Gil Refael, Michael H. Freedman: Robust Majorana magic gates via measurements, Phys. Rev. B 99 (2019) 144521 [doi:10.1103/PhysRevB.99.144521, arXiv:1812.10498]
See also:
- Yusuke Masaki, Takeshi Mizushima, Muneto Nitta, Non-Abelian Anyons and Non-Abelian Vortices in Topological Superconductors arXiv:2301.11614
Discussion via AdS/CFT
Discussion of superconductivity via AdS/CFT in condensed matter physics:
-
Sean Hartnoll, Christopher Herzog, Gary Horowitz, Building an AdS/CFT superconductor, Phys. Rev. Lett. 101:031601, 2008 (arXiv:0803.3295)
-
Alberto Salvio, Superconductivity, Superfluidity and Holography (arXiv:1301.0201)
-
Rong-Gen Cai, Li Li, Li-Fang Li, Run-Qiu Yang, Introduction to Holographic Superconductor Models, Sci China-Phys Mech Astron, 2015, 58(6):060401 (arXiv:1502.00437)
-
Sean Hartnoll, Andrew Lucas, Subir Sachdev, Section 6.3 of: Holographic quantum matter, MIT Press 2018 (arXiv:1612.07324, publisher)
-
Yiqian Chen, Xiaobo Guo, Peng Wang, Holographic Superconductors in a Non-minimally Coupled Einstein-Maxwell-scalar Model (arXiv:2111.03810)
-
Chuan-Yin Xia, Hua-Bi Zeng, Yu Tian, Chiang-Mei Chen, Jan Zaanen, Holographic Abrikosov lattice: vortex matter from black hole (arXiv:2111.07718)
-
Dong Wang, Xiongying Qiao, Qiyuan Pan, Chuyu Lai, Jiliang Jing, Holographic entanglement entropy and complexity for the excited states of holographic superconductors [arXiv:2301.00513]
(in relation to holographic entanglement entropy)
-
Chi-Hsien Tai, Wen-Yu Wen, A study of layered holographic superconductor [arXiv:2405.07535]
-
Souvik Paul, Sunandan Gangopadhyay: Noncommutative -wave holographic superconductors [arXiv:2502.08275]
-
Zhenguo Wang, Xian-Hui Ge, Shuta Ishigaki: Dependence of the critical temperature and disorder in holographic superconductors on superfluid density [arXiv:2312.16029^rbrack;
High -superconductivity
Via topological phases of matter:
- M. C. Diamantini, C. A. Trugenberger, V. M. Vinokur, Topological Nature of High Temperature Superconductivity (arXiv:2009.01763)
Doping semiconductors to superconductors
On doping of semiconductors to become superconducting:
-
Patrick J. Strohbeen, Aurelia M. Brook, Wendy L. Sarney, Javad Shabani: Superconductivity in hyperdoped by molecular beam epitaxy, AIP Advances 13 085118 (2023) [arXiv:2305.04610, doi:10.1063/5.0157509]
-
Javad Shabani et al.: Coherent Superconductor-Semiconductor Epitaxy for Integrated Quantum Electronics [arXiv:2412.15421]
Last revised on May 4, 2025 at 08:38:29. See the history of this page for a list of all contributions to it.