nLab non-perturbative effect
Contents
Idea
An effect in non-perturbative quantum field theory that cannot be seen in perturbative quantum field theory is called a non-perturbative effect.
More in detail, theories with instanton field configurations (such as in Yang-Mills theory, hence in QCD and QED) or branes (such as in string theory), etc., are expected to have observables which as functions of the coupling constant are transseries of the form
where the first sum is the Feynman perturbation series itself and where the terms with a non-analytic dependence of the form or are the contributions of the instantons. Since all the derivatives of the functions or vanish at coupling constant , the Taylor series of this part of the observable does not appear in perturbative QFT, even though it is present. Therefore this is called a non-perturbative effect.
Related is resurgence theory. See also at perturbation theory – Divergence/convergence for more.
Notice that, while non-perturbative effects are generally the least understood, they are not exotic but ubiquitous: Essentially the entire parameter space of a generic “physical theory” is non-perturbative. In fact, the non-perturbative region of parameter space is the complement of an infinitesimally thickened point (labeled “perturbative” in the following graphics):
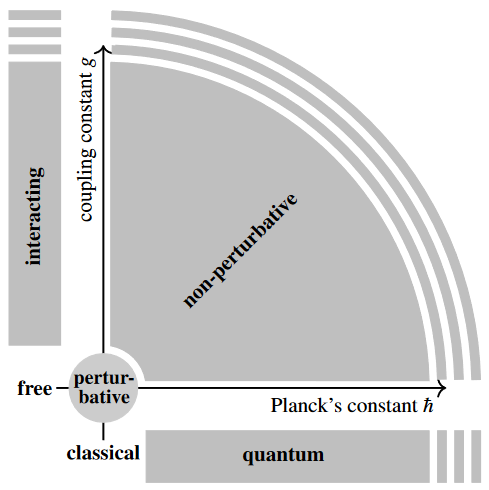
Examples
Schwinger effect
Confinement and the mass gap
A central example of a non-perturbative effect is confinement (hence the “mass gap problem”) in Yang-Mills theory at low temperature. Perturbation theory is not suited to explain this (e.g Espiru 94, section 7).
Quark-gluon plasma
At the other extreme of high temperature QCD, also the quark-gluon plasma, while now deconfined is thought to be strongly coupled.
Hadronic physics in flavour and anomalies
Non-perturbative effects in hadron-physics affects the discussion of possible beyond-standard model physics as seen in
Worldsheet and brane instantons in string/M-theory
-
, the Planck length in 11-dimensions;
-
the length (circumference) of the circle fiber for KK-compactification to 10 dimensions
and the string theory scales
-
, the string length scale;
-
, the string coupling constant of perturbative string theory.
Then under the duality between M-theory and type IIA string theory these scales are related as follows:
equivalently
equivalently
Hence a membrane instanton, which on a 3-cycle gives a contribution
becomes
-
if the cycle wraps, , a worldsheet instanton
-
the cycle does not wrap, a spacetime instanton contribution, specifically a D2-brane instanton?
(This unification of the two different non-perturbative effects in perturbative string theory (worldsheet instantons and spacetime instantons), to a single type of effect (membrane instanton) in M-theory was maybe first made explicit in Becker-Becker-Strominger 95. Brief review includes Marino 15, sections 1.2 and 1.3).
Related concepts
References
In field theory
- Alexander P. Bakulev, Dmitry Shirkov, Inevitability and Importance of Non-Perturbative Elements in Quantum Field Theory, Proceedings of the 6th Mathematical Physics Meeting, Sept. 14–23, 2010, Belgrade, Serbia, pp. 27–54, Belgrade Institute of Physics [arXiv:1102.2380, ISBN 978-86-82441-30-4, book webpage]
Discussion of traditional algebraic quantum field theory as being about non-perturbative effects (and therefore lacking any interesting models in 3+1 dimensions, so far…):
- Franco Strocchi, An Introduction to Non-Perturbative Foundations of Quantum Field Theory, Oxford University Press (2013) [doi:10.1093/acprof:oso/9780199671571.001.0001]
Genral introduction and toy examples (e.g. phi^4-theory or anharmonic oscillator):
-
Mario Flory, Robert C. Helling, Constantin Sluka, Section 2 of: How I Learned to Stop Worrying and Love QFT (arXiv:1201.2714)
Discussion for phi^4 theory is in
- Marco Serone, from 2:46 on in A look at using perturbation theory, January 2018 (recording)
Discussion for QCD:
- Marcos Mariño: Instantons and Large – An Introduction to Non-Perturbative Methods in QFT, Cambridge University Press (2015) [doi:10.1017/CBO9781107705968, pdf]
and for (super-)Yang-Mills theory and string theory:
-
Marcos Mariño, Lectures on non-perturbative effects in large N gauge theories, matrix models and strings, Fortschritte der Physik 62 5‐6 (2014) 455-540 [arXiv:1206.6272]
-
Marcos Mariño: Non-perturbative effects in string theory and AdS/CFT, Spring School on Superstring Theory and Related Topics 2015 [pdf, pdf, recording]
In QCD (hadrodynamics) via operator product expansion:
- Mikhail Shifman, OPE-based Methods in Nonperturbative QCD, Eur. Phys. J. C (2022) [arXiv:2208.10600]
In phenomenology
-
Ulrich Nierste, Flavour Anomalies: Phenomenology and BSM Interpretations, 2018 (pdf)
-
Fred Jegerlehner, The Role of Mesons in Muon (arXiv:1809.07413)
In cosmology
In cosmology:
- Anna Ijjas, Frans Pretorius, Paul Steinhardt, Stability and the gauge problem in non-perturbative cosmology, Journal of Cosmology and Astroparticle Physics, Volume 2019, January 2019 (arXiv:1809.07010, doi:10.1088/1475-7516/2019/01/015)
In string theory
The form of the contribution of non-perturbative effects in string theory was originally observed in
- Stephen Shenker, The Strength of nonperturbative effects in string theory, presented at the Cargese Workshop on Random Surfaces, Quantum Gravity and Strings, Cargese, France, May 1990 (spire)
The interpretation via D-branes of non-perturbative effects in the string coupling constant is due to
- Joseph Polchinski, Combinatorics of boundaries in string theory, Phys. Rev. D 50, 6041 (1994) (arXiv:hep-th/9407031)
The identification of non-perturbative contributions in string theory with brane contributions is due to
- Katrin Becker, Melanie Becker, Andrew Strominger, Five-branes, membranes and nonperturbative string theory, Nucl. Phys. B 456, 130 (1995) (hep-th/9507158)
Review includes
Reviews specifically in type II string theory include
-
Hugo Looyestijn, Non-perturbative effects in type IIA string theory, Master Thesis 2006 (pdf)
-
Angel Uranga, Non-perturbative effects and D-brane instanton resummation in string theory (pdf, pdf)
In M-Theory
The relation of non-perturbative effects in string theory to M-theory goes back to
- Edward Witten, section 2.2 of String Theory Dynamics In Various Dimensions, Nucl.Phys.B443:85-126,1995 (arXiv:hep-th/9503124)
In Becker-Becker-Strominger 95 it was realized that the worldsheet instantons and D-brane instantons of string theory unify to membrane instantons (see Marino 15, section 1.3)
Last revised on June 24, 2025 at 10:51:18. See the history of this page for a list of all contributions to it.