nLab quark-gluon plasma
Context
Fields and quanta
fields and particles in particle physics
and in the standard model of particle physics:
matter field fermions (spinors, Dirac fields)
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
(also: antiparticles)
hadrons (bound states of the above quarks)
minimally extended supersymmetric standard model
bosinos:
dark matter candidates
Exotica
Contents
Idea
The quark-gluon plasma is the phase of matter of quantum chromodynamics at extremely high temperature. At high temperature quarks are not confined to hadron bound states but propagate freely together with the gluons, forming a “quark-gluon soup”. Since this is analogous to an ordinary plasma which is a phase where electrons and protons are no longer bound to atoms but propagate freely, one speaks of quark-gluon plasma.
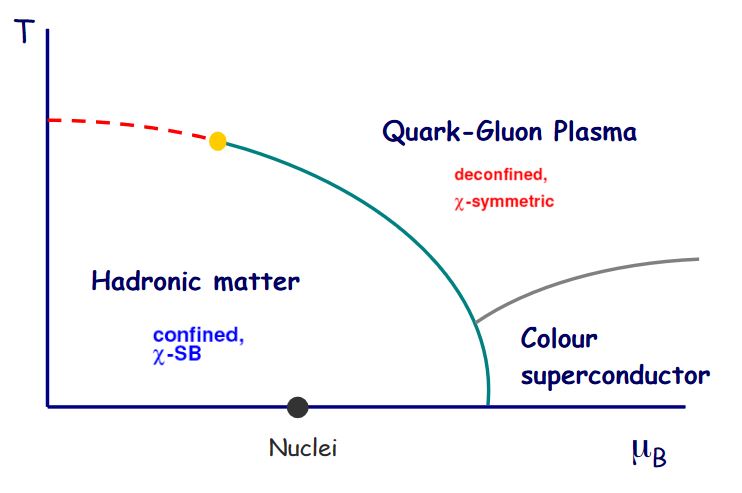
Schematic phase diagram of QCD. The vertical axis indicates temperature , the horizontal axis indicates baryon density. At low enough temperature quarks and gluons only appear as hadron bound states (confinement). But above a critical temperature these hadron bound states break apart (deconfinement) and quarks and gluons may exist freely. This phase of QCD is the quark-gluon plasma.
graphics grabbed from Blaizot 03.
Non-perturbative regime
Despite the deconfinement beyond temperature , the quark-gluon plasma at temperature as produced in experiment (Adams et al. 05, Adcox et al. 05) is apparently strongly coupled, meaning that its properties are non-perturbative effects requiring discussion of QCD as a non-perturbative field theory. With an exact such theory largely missing, much of the theoretical discussion of the quark-gluon plasma involves lattice QCD computer simulation. Indication for strong coupling of the QG-plasma comes from the nature of the elliptic flow seen both in experiment as well as in these computer simulations, which shows hydrodynamic behaviour with extremely small shear viscosity (e.g. Shuryak 01, Chakraborty 12).
It has been proposed (Policastro-Son-Starinets 01) that, therefore, an analytic approach to a description of the quark-gluon plasma (i.e. not just via lattice QCD computer experiment) might be given by approximate AdS-CFT duality, hence by the AdS/QCD correspondence or fluid/gravity correspondence (see e.g. Biagazzi-Cotrone 12). The difficulty with this approach is that for QCD (as opposed to N=4 D=4 SYM) AdS-CFT duality applies only to some approximation, see at AdS/QCD correspondence for more.
Perturbative regime
At yet higher energies, the quark-gluon plasma is eventually supposed to be weakly coupled again, due to asymptotic freedom (e.g. Blaizot 03)
Properties
Early cosmology and nucleosynthesis
In the standard model of cosmology a quark gluon plasma filled the universe about comoving seconds after the Big Bang. Decrease of temperature then led to the quark-gluon plasma condensing out to form hadrons and in particular baryons and hence in particular nucleons (protons and neutrons) and eventually atomic nuclei (cosmic nucleosynthesis).
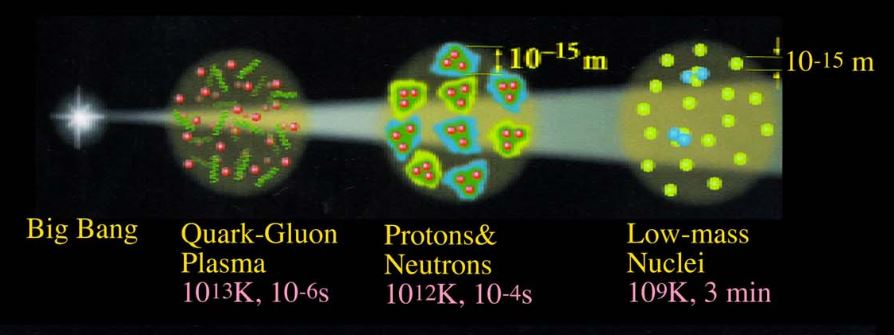
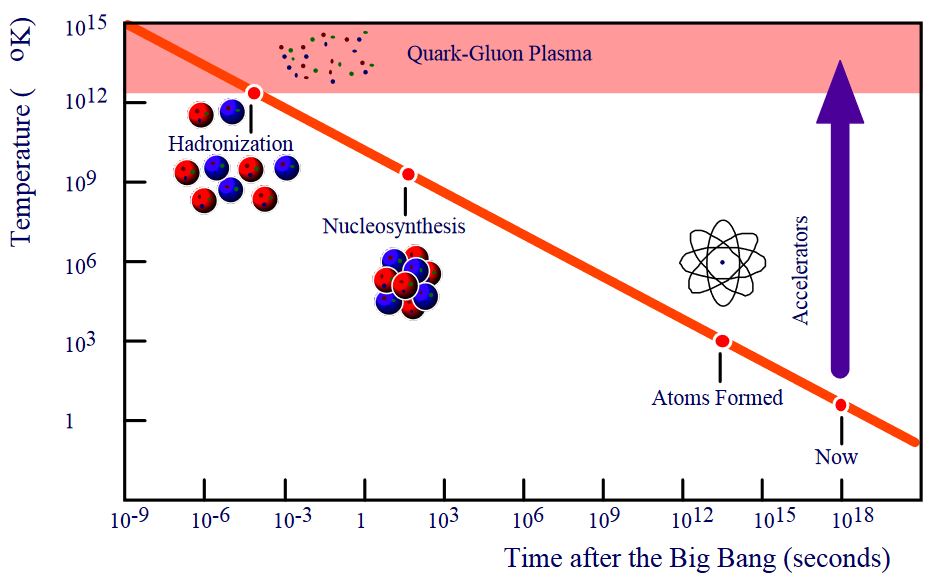
graphics grabbed from Haseeb 09
See the references below.
Related concepts
-
The quark-gluon plasma is naturally studied in terms of infinite-temperature thermal field theory (Blaizot-Iancu-Rebhan 03, section 2.2.4, Blaizot 04, around p. 17)
-
the QCD trace anomaly affects the equation of state of the quark-gluon plasma.
-
In as far as the quark-gluon plasma is described by fluid dynamics, the fluid/gravity correspondence applies.
References
General
-
Stanislaw Mrowczynski, Quark-Gluon Plasma, Acta Phys. Polon. B 29 (1998) 3711 [arXiv:nucl-th/9905005]
-
Mahnaz Q. Haseeb, Introduction to Quark Gluon Plasma, 2009 (pdf)
-
Roman Pasechnik, Michal Šumbera, Phenomenological Review on Quark-Gluon Plasma: Concepts vs. Observations, Universe 2017, 3(1), 7 (arXiv:1611.01533)
-
Jean-Paul Blaizot, Edmond Iancu, Anton Rebhan, Thermodynamics of the high temperature quark gluon plasma, Quark–Gluon Plasma 3, pp. 60-122 (2004) (arXiv:hep-ph/0303185, spire:615570)
-
Jean-Paul Blaizot, around p. 17 of Thermodynamics of the high temperature Quark-Gluon Plasma, AIP Conf. Proc. 739, 63-96 (2004) (doi:10.1063/1.1843592)
-
Jacopo Ghiglieri, Aleksi Kurkela, Michael Strickland, Aleksi Vuorinen, Perturbative Thermal QCD: Formalism and Applications (arXiv:2002.10188)
-
W. Busza, W.A. Zajc: The Early History of the Quark-Gluon Plasma [arXiv:2504.08720]
See also
- Wikipedia, Quark-Gluon plasma
On the rho-meson and its chiral partner a1-meson in the quark-gluon plasma:
- Robert Pisarski, Where does the Rho Go? Chirally Symmetric Vector Mesons in the Quark-Gluon Plasma, Phys. Rev. D52 (1995) 3773-3776 (arXiv:hep-ph/9503328)
Non-perturbative aspects
Discussion of non-perturbative effects in QCD:
-
Edward Shuryak, Nonperturbative QCD and Quark-Gluon Plasma, lectures at Trieste, 2001 (pdf)
-
Purnendu Chakraborty, Non-perturbative aspects of quark gluon plasma above deconfinement temperature, Proceedings of the DAE Symp. on Nucl. Phys. 57 (2012) (pdf)
Further discussion in relation to instantons in QCD includes
- Nikolai Kochelev, Ultra-light Glueballs in Quark-Gluon Plasma (arXiv:1501.07002)
Experimental realization
Realization of the quark-gluon plasma at the RHIC experiment has tentatively been claimed in
-
John Adams, et al. Experimental and theoretical challenges in the search for the quark–gluon plasma: The STAR Collaboration’s critical assessment of the evidence from RHIC collisions. Nuclear Physics A 757.1-2 (2005): 102-183.
-
K. Adcox, et al., Formation of dense partonic matter in relativistic nucleus–nucleus collisions at RHIC: experimental evaluation by the PHENIX collaboration Nuclear Physics A 757.1-2 (2005): 184-283.
Exposition and review:
- Maria Elena Tejeda-Yeomans, Heavy-ion physics: freedom to do hot, dense, exciting QCD (arXiv:2004.13812)
Status report:
- Dynamics of Hot QCD Matter – Current Status and Developments [arXiv:2208.13440]
In early universe cosmology
Discussion of the quark gluon-plasma in cosmology as the phase of matter shortly after the big bang:
-
Edward Witten, Cosmic Separation Of Phases, Phys. Rev. D30, 272 (1984) (doi:10.1103/PhysRevD.30.272)
-
Dominik J. Schwarz, The first second of the Universe, Annalen Phys.12:220-270, 2003 (arXiv:astro-ph/0303574)
-
K. Sakthi Murugesan, G. Janhavi, and P. R. Subramanian, Can the phase transition from quark-gluon plasma to hadron-resonance gas affect primordial nucleosynthesis?, Phys. Rev. D 41, 2384 (doi:10.1103/PhysRevD.41.2384)
-
K. Sakthi Murugesan, G. Janhavi, and P. R. Subramanian, Importance of interactions in quark-gluon plasma: Baryon-number density contrast and primordial nucleosynthesis, Phys. Rev. D 42, 3576 (1990) (arXiv:10.1103/PhysRevD.42.3576)
-
Keith Olive, The Quark - hadron transition in cosmology and astrophysics, Science 251, 1194 (1991)
-
A.A. Coley, T. Trappenberg, The Quark-Hadron Phase Transition, QCD Lattice Calculations and Inhomogeneous Big-Bang Nucleosynthesis, Phys.Rev. D50 (1994) 4881-4885 (arXiv:astro-ph/9307031)
-
Hideo Suganuma, Hiroko Ichie, Hideko Monden, Shoichi Sasaki, Manabu Orito, Tadahiro Yamamoto, Toshitaka Kajino, QCD Phase Transition at high Temperature in Cosmology (arXiv:hep-ph/9608333)
-
Deepak Chandra, Ashok Goyal, Dynamical evolution of the Universe in the quark-hadron phase transition and possible nugget formation, Phys.Rev. D62 (2000) 063505 (arXiv:hep-ph/9903466)
-
N. Borghini, W. N. Cottingham, R. Vinh Mau, Possible Cosmological Implications of the Quark-Hadron Phase Transition, J.Phys.G26:771, 2000 (arXiv:hep-ph/0001284)
-
Joseph I Kapusta, Quark-Gluon Plasma in the Early Universe, in Phase Transitions in the Early Universe: Theory and Observations Springer, Dordrecht, 2001. 103-121 (arXiv:astro-ph/0101516)
-
Michael McGuigan, Wolfgang Söldner, QCD Cosmology from the Lattice Equation of State (arXiv:0810.0265, spire:798226)
The effect of the strong interactions on cosmology was considered early on [10, 11] but the nonperturbative nature of the strong interactions at low energy limited the progress of the subject.
-
S. M. Blinder, Evolution of Matter from a Quark-Gluon Plasma, Wolfram Demonstration Project, 2011
-
The liquid universe – quark-gluon plasma and the creation of matter (pdf)
-
Sz. Borsanyi, Z. Fodor, K. H. Kampert, S. D. Katz, T. Kawanai, T. G. Kovacs, S. W. Mages, A. Pasztor, F. Pittler, J. Redondo, A. Ringwald, K. K. Szabo, Lattice QCD for Cosmology (arXiv:1606.07494)
Description via geometric engineering of QCD on intersecting branes
Description via geometric engineering of QCD on intersecting branes (“holographic QCD” see also at string theory results applied elsewhere):
Exposition and review:
-
Pavel Kovtun, Quark-Gluon Plasma and String Theory, RHIC news (2009) (blog entry)
-
Makoto Natsuume, String theory and quark-gluon plasma (arXiv:hep-ph/0701201)
-
Steven Gubser, Using string theory to study the quark-gluon plasma: progress and perils (arXiv:0907.4808)
-
Francesco Biagazzi, A. Cotrone, Holography and the quark-gluon plasma, AIP Conference Proceedings 1492, 307 (2012) (doi:10.1063/1.4763537, slides pdf)
-
Brambilla et al., section 9.2.2 of QCD and strongly coupled gauge theories - challenges and perspectives, Eur Phys J C Part Fields. 2014; 74(10): 2981 (doi:10.1140/epjc/s10052-014-2981-5)
-
Jorge Casalderrey-Solana, Hong Liu, David Mateos, Krishna Rajagopal, Urs Achim Wiedemann, Gauge/string duality, hot QCD and heavy ion collisions, Cambridge University Press, 2014 (arXiv:1101.0618)
-
Makoto Natsuume, Section 12 in: AdS/CFT Duality User Guide, Lecture Notes in Physics 903, Springer (2015) [arXiv:1409.3575, doi:10.1007/978-4-431-55441-7]
and specifically via “improved holographic QCD”
- Umut Gürsoy, Elias Kiritsis, Liuba Mazzanti, Georgios Michalogiorgakis, Francesco Nitti, Improved Holographic QCD, Lect. Notes Phys. 828 (2011) 79-146 [arXiv:1006.5461]
Holographic discussion of the shear viscosity of the quark-gluon plasma goes back to
- Giuseppe Policastro, D.T. Son, A.O. Starinets, Shear viscosity of strongly coupled supersymmetric Yang-Mills plasma, Phys. Rev. Lett. 87 081601 (2001) [arXiv:hep-th/0104066]
Other original articles include:
-
Brett McInnes, Holography of the Quark Matter Triple Point (arXiv:0910.4456)
-
Hovhannes R. Grigoryan, Paul M. Hohler, Mikhail A. Stephanov, Towards the Gravity Dual of Quarkonium in the Strongly Coupled QCD Plasma (arXiv:1003.1138)
-
Mansi Dhuria, Aalok Misra, Towards MQGP, JHEP 1311 (2013) 001 (arXiv:1306.4339)
-
Sara Heshmatian, Razieh Morad, Jet suppression in non-conformal plasma using AdS/CFT (arXiv:1812.09374)
-
Irina Ya. Aref’eva, Kristina Rannu, Pavel Slepov, Energy Loss in Holographic Anisotropic Model for Heavy Quarks in External Magnetic Field (arXiv:2012.05758)
With emphasis on application to neutron stars:
-
Carlos Hoyos, Niko Jokela, Matti Järvinen, Javier G. Subils, Javier Tarrio, Aleksi Vuorinen, Transport in strongly coupled quark matter, Phys. Rev. Lett. 125 (2020) 241601 7Lbrack;arXiv:2005.14205, doi:10.1103/PhysRevLett.125.241601]
-
Carlos Hoyos, Niko Jokela, Matti Järvinen, Javier G. Subils, Javier Tarrio, Aleksi Vuorinen, Holographic approach to transport in dense QCD matter, Phys. Rev. D 105 6 (2022) 066014 [arXiv:2109.12122, doi:10.1103/PhysRevD.105.066014]
See also:
-
Alfonso Ballon-Bayona, Luis A. H. Mamani, Alex S. Miranda, Vilson T. Zanchin, Effective holographic models for QCD: Thermodynamics and viscosity coefficients (arXiv:2103.14188)
-
Nelson R. F. Braga, Octavio C. Junqueira, Hawking-Page transition in holographic QCD at finite density, Phys. Lett. B 855 (2024) 138813 [arXiv:2404.04683, doi:10.1016/j.physletb.2024.138813]
-
Niko Jokela, Matti Järvinen, Aleksi Piispa, Refining holographic models of the quark-gluon plasma [arXiv:2405.02394]
“Holographic QCD has reached the level of sophistication that allows for a detailed reproduction of numerous lattice QCD outcomes”
-
Tuna Demircik, Niko Jokela, Matti Järvinen, Aleksi Piispa, Is holographic quark-gluon plasma homogeneous? [arXiv:2405.02392]
Last revised on April 14, 2025 at 18:25:09. See the history of this page for a list of all contributions to it.