nLab anomalous magnetic moment

Idea

In perturbative quantum field theory, the magnetic moment of particles as predicted by classical field theory may receive corrections due to quantum effects. Such corrections are also called quantum anomalies, and hence one speaks of the anomalous magnetic moments, traditionally denoted by “$g-2$”.

The archetypical example is the anomalous magnetic moment of the electron in quantum electrodynamics, which is famous as the pQFT-prediction that matches experiment to an accuracy of about $10^{-12}$ (e.g.Scharf 95, (3.10.20)).

Similarly there is the anomalous magenetic moment $g_\mu - 2$ of the muon and the other leptons.

Anomalies

In fact, the anomalous magnetic moment of the muon $g_\mu - 2$ has become notorious for apparently showing a noticeable discrepancy between theoretic prediction from the standard model of particle physics and its value as determined in experiment. The discrepancy is now found to have statistical significance around 3.5σ (DHMZ 17) or 4σ (Jegerlehner 18a).

In April 2021, after re-doing the Brookhaven experiment, Fermilab confirms these findings and states a statistical significance of the deviation of 4.2 sigma (Abi et al. 21).

Recent measurements may even show a possible deviation around 2.5 σ for the electron’s anomalous magnetic moment (see Falkowski 18). Details depend on understanding of non-perturbative effects (Jegerlehner 18b, section 2).

In particular, there seems to be inconsistencies in the theoretical understanding of the relevant lattice QCD-computations:

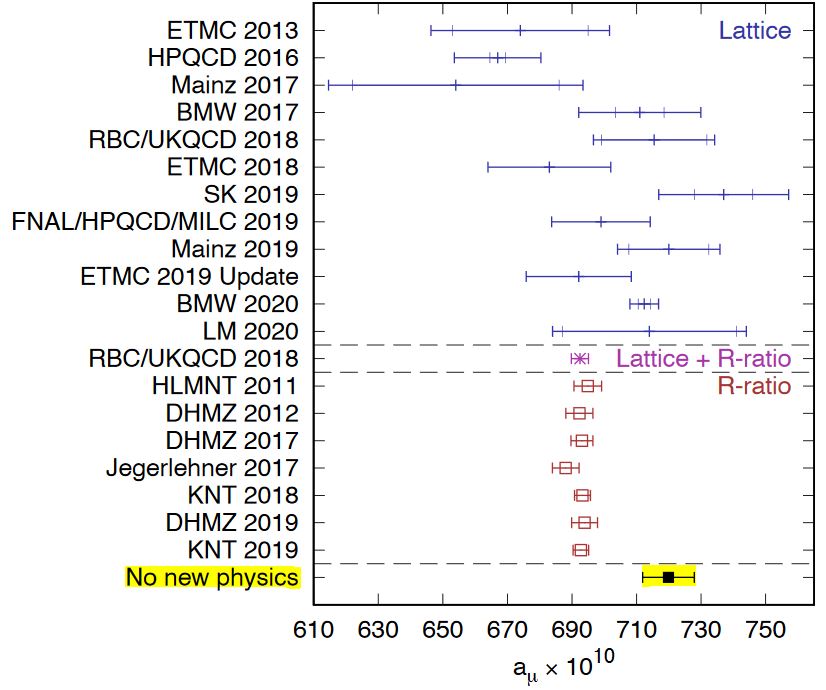
graphics from Lehner-Meyer 20, Fig 14

If these experimental “anomalies” (in the sense of phenomenology) in the anomalous magnetic moment $g_\mu - 2$ (and possibly even in $g_e -2$) are real (the established rule of thumb is that deviations are established once their statistical significance reaches 5σ, see here), they point to “new physics” beyond the standard model of particle physics.

In fact Lyons 13b argued that the detection-threshold of the statistical significance of anomalies here should be just 4σ, which would mean that they should already count as being detected:

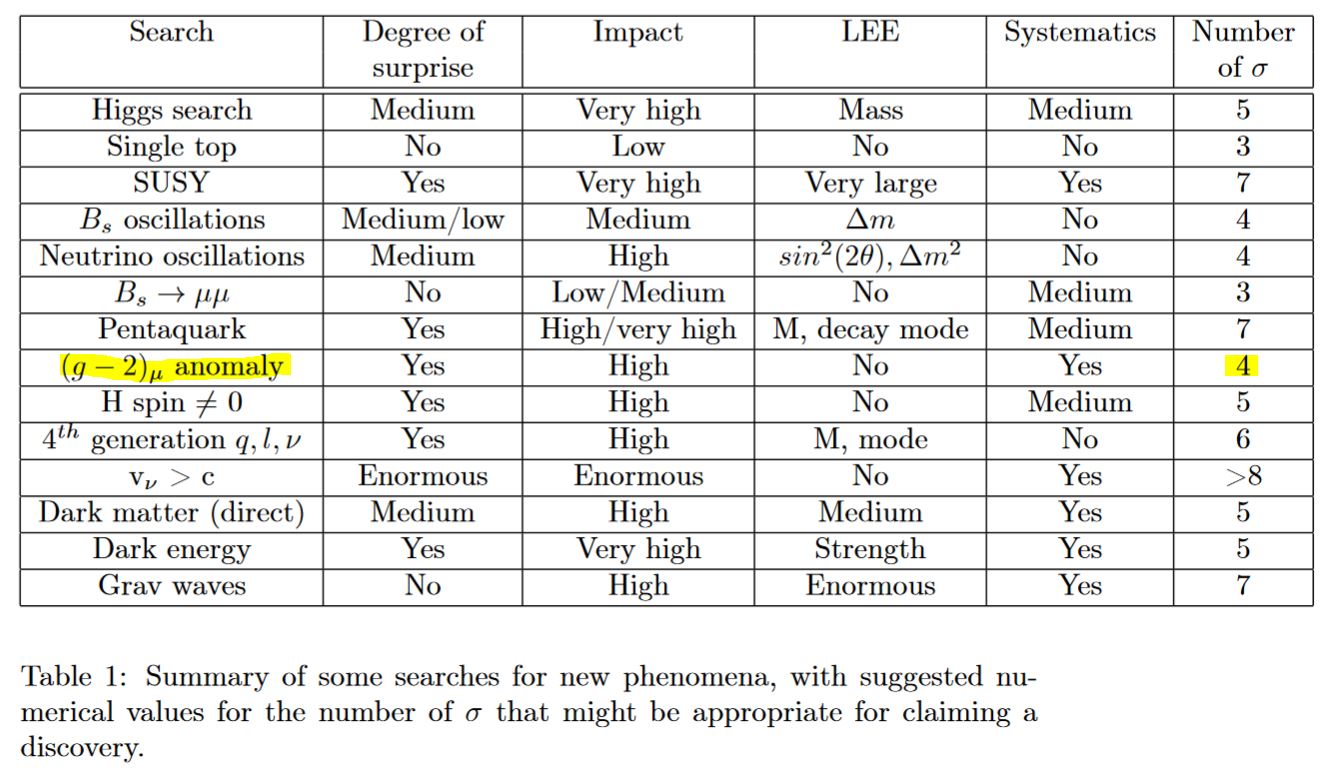
table taken from Lyons 13b, p. 4

Together with the flavour anomalies, these anomalies relate to the flavour problem in the standard model of particle physics:

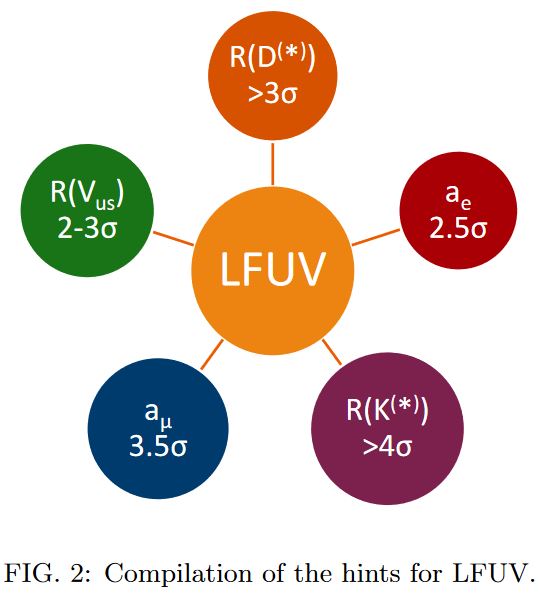
graphics from Crivellin-Hoferichter 20

(here “$R$” refers to flavour anomalies in various channels, “$a$” refers to anomalies in the the anomalous magnetic moments of the electron and the muon, “LFUV” is shoft for “Lepton Flavor Universality Violation”, and the numbers are the statistical significances of the effects seen)

Possible explanations for the anomalies in the anomalous magnetic moments is the existence of leptoquarks (Bauer-Neubert 15, CCDM 16, Falkowski 17, Müller 18), which at the same time are a candidate for explaining the flavour anomalies (see also Chiang-Okada 17).

Contributions

QED contributions

(…) for the electron see e.g. Scharf 95, section 3.10 (…)

Quantum gravity contributions

The further corrections of 1-loop perturbative quantum gravity to the anomalous magnetic moment of the electron and the muon have been computed in (Berends-Gastman 75) and found to be finite without need for renormalization. These Feynman diagrams contribute:

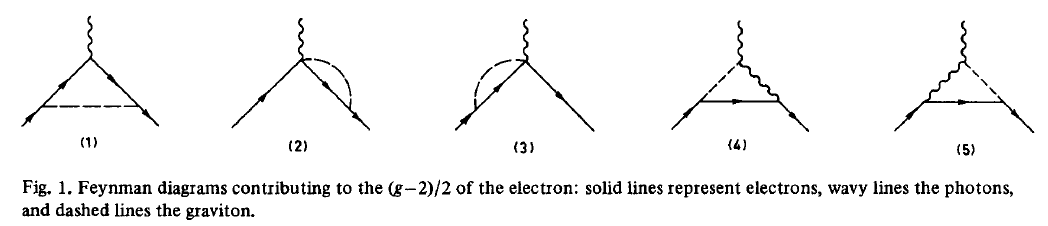
Axion contributions

Possible contributions to and xconstraints on $g_{lep}-2$ from hypothetical axions are discussed in ACGM 08, MMPP 16, BNT 17…

Related concepts

• electric dipole moment

References

General

Basic discussion:

• Othmar Steinmann, What is the Magnetic Moment of the Electron?, Commun.Math.Phys. 237 (2003) 181-201 (arXiv:hep-ph/0211187)

• Kirill Melnikov, Arkady Vainshtein, Theory of the Muon Anomalous Magnetic Moment, Springer Tracts in Modern Physics 216, 2006

• Friedrich Jegerlehner, The Anomalous Magnetic Moment of the Muon, Springer Tracts in Modern Physics 226, Springer-Verlag Berlin Heidelberg, 2008

• Song Li, Yang Xiao, Jin Min Yang, A pedagogical review on muon $g-2$, Modern Physics 4 (2021) 40-47 (arXiv:2110.04673)

Discussion of detection-threshold for the statistical significance of anomalies:

• Louis Lyons, Discovering the Significance of 5 sigma (arXiv:1310.1284)

See also

• Wikipedia, Anomalous magnetic dipole moment

Prediction to loop order 5 in QED:

• Tatsumi Aoyama, Masashi Hayakawa, Toichiro Kinoshita, Makiko Nio, Tenth-Order QED Contribution to the Electron $g-2$ and an Improved Value of the Fine Structure Constant, Phys. Rev. Lett. 109, 111807 (arXiv:1205.5368, doi:10.1103/PhysRevLett.109.111807)

Comprehensive discussion for the muon:

• T. Aoyama et al., The anomalous magnetic moment of the muon in the Standard Model (arXiv:2006.04822)

  Discussion up to 12th loop order in section 6.3.

• Alex Keshavarzi, Kim Siang Khaw, Tamaki Yoshioka, Muon $g-2$: current status (arXiv:2106.06723)

Experiment and deviation

Discussion of precision experiment and possible deviation from theory:

• Michel Davier, Andreas Hoecker, Bogdan Malaescu, Zhiqing Zhang, Reevaluation of the hadronic vacuum polarisation contributions to the Standard Model predictions of the muon g-2 and alpha(mZ) using newest hadronic cross-section data, Eur. Phys. J. C (2017) 77: 827 (arXiv:1706.09436)

• J. L. Holzbauer on behalf of the Muon g-2 collaboration, The Muon g-2 Experiment Overview and Status, Proceedings for The 19th International Workshop on Neutrinos from Accelerators (NUFACT 2017) (arXiv:1712.05980)

• Fred Jegerlehner, The Muon g-2 in Progress, Acta Physica Polonica 2018 (doi:10.5506/APhysPolB.49.1157, arXiv:1804.07409)

• Fred Jegerlehner, The Role of Mesons in Muon $g-2$ (arXiv:1809.07413)

• Adam Falkowski, Both $g-2$ anomalies, June 2018

• B. Abi et al. (Muon g−2 Collaboration), Measurement of the Positive Muon Anomalous Magnetic Moment to 0.46 ppm, Phys. Rev. Lett. 126, 141801 2021 (doi:10.1103/PhysRevLett.126.141801)

  $\,$

  Exposition:

  Priscilla Cushman, Muon’s Escalating Challenge to the Standard Model, Physics 14, 54, April 2021 (web)

• Maarten Golterman, Theory review for hadronic corrections to $g-2$ [arXiv:2208.05560]

• Ashutosh Kotwal, Joaquim Matias, Andrea Mauri, Tom Tong, Lukas Varnhorst, Round table on Standard Model Anomalies [arXiv:2211.13030]

Relation to flavour anomalies

Possible explanation of the anomaly in the anomalous magnetic moments in terms of leptoquarks:

• Martin Bauer, Matthias Neubert, One Leptoquark to Rule Them All: A Minimal Explanation for $R_{D^{(\ast)}}$, $R_K$ and $(g-2)_\mu$, Phys. Rev. Lett. 116, 141802 (2016) (arXiv:1511.01900)

• Estefania Coluccio Leskow, Andreas Crivellin, Giancarlo D’Ambrosio, Dario Müller, $(g-2)_\mu$, Lepton Flavour Violation and Z Decays with Leptoquarks: Correlations and Future Prospects, Phys. Rev. D 95, 055018 (2017) (arXiv:1612.06858)

• Anirban Biswas, Avirup Shaw, Reconciling dark matter, $R_{K^{(\ast)}}$ anomalies and $(g-2)_\mu$ in an $L_\mu-L_\tau$ scenario (arXiv:1903.08745)

• Adam Falkowski, Leptoquarks strike back, November 2017

• Cheng-Wei Chiang, Hiroshi Okada, A simple model for explaining muon-related anomalies and dark matter (arXiv:1711.07365)

• Dario Müller, Leptoquarks in Flavour Physics, EPJ Web of Conferences 179, 01015 (2018) (arXiv:1801.03380)

• Junichiro Kawamura, Stuart Raby, Andreas Trautner, Complete Vector-like Fourth Family and new $U(1)'$ for Muon Anomalies (arXiv:1906.11297)

Further possible joint explanation of the anomalies observed in the muon anomalous magnetic moment and the flavour anomalies:

• Geneviève Bélanger, Cédric Delaunay, Susanne Westhoff, A Dark Matter Relic From Muon Anomalies, Phys. Rev. D 92, 055021 (2015) (arXiv:1507.06660)

• Cheng-Wei Chiang, Hiroshi Okada, A simple model for explaining muon-related anomalies and dark matter (arXiv:1711.07365)

• Junichiro Kawamura, Stuart Raby, Andreas Trautner, Complete Vector-like Fourth Family and new $U(1)'$ for Muon Anomalies (arXiv:1906.11297)

• Lorenzo Calibbi, M.L. López-Ibáñez, Aurora Melis, Oscar Vives, Muon and electron $g-2$ and lepton masses in flavor models (arXiv:2003.06633)

• A. S. de Jesus, S. Kovalenko, F. S. Queiroz, K. Sinha, C. Siqueira, Vector-Like Leptons and Inert Scalar Triplet: Lepton Flavor Violation, $g-2$ and Collider Searches (arXiv:2004.01200)

• Shaikh Saad, Combined explanations of $(g-2)_\mu$, $R_{D^\ast}$, $R_{K^\ast}$ anomalies in a two-loop radiative neutrino mass model (arXiv:2005.04352)

• Da Huang, António P. Morais, Rui Santos, Anomalies in $B$ Decays and Muon $g-2$ from Dark Loops (arXiv:2007.05082)

• K.S. Babu, P.S. Bhupal Dev, Sudip Jana, Anil Thapa, Unified Framework for $B$-Anomalies, Muon $g-2$, and Neutrino Masses (arXiv:2009.01771)

• Sang Quang Dinh, Hieu Minh Tran, Muon $g-2$ and semileptonic $B$ decays in BDW model with gauge kinetic mixing (arXiv:2011.07182)

• Mingxuan Du, Jinhan Liang, Zuowei Liu, Van Que Tran, A vector leptoquark interpretation of the muon $g-2$ and $B$ anomalies (arXiv:2104.05685)

A leptoquark model meant to address all of the flavour anomalies, the (g-2)-anomaly and the Cabibbo anomaly at once:

• David Marzocca, Sokratis Trifinopoulos, A Minimal Explanation of Flavour Anomalies: B-Meson Decays, Muon Magnetic Moment, and the Cabbibo Angle (arXiv:2104.05730)

Realization in F-theory of GUT-models with Z'-bosons and/or [leptoquarks]] addressing the flavour anomalies and the (g-2) anomalies:

• Miguel Crispim Romao, Stephen F. King, George K. Leontaris, Non-universal $Z'$ from Fluxed GUTs, Physics Letters B Volume 782, 10 July 2018, Pages 353-361 (arXiv:1710.02349)

• A. Karozas, G. K. Leontaris, I. Tavellaris, N. D. Vlachos, On the LHC signatures of $SU(5) \times U(1)'$ F-theory motivated models (arXiv:2007.05936)

QED contributions

The computation of the anomalous magnetic dipole moment of the electron in QED is spelled out (via causal perturbation theory) in

• Günter Scharf, section 3.10, culminating in (3.10.20), of Finite Quantum Electrodynamics – The Causal Approach, Berlin: Springer-Verlag, 1995, 2nd edition

QCD contribution

General

Discussion of QCD contributions via lattice QCD:

• Christoph Lehner, Aaron S. Meyer, Consistency of hadronic vacuum polarization between lattice QCD and the R-ratio (arXiv:2003.04177)

Via holographic QCD

Application of holographic QCD to anomalous magnetic moment of the muon:

• Luigi Cappiello, What does Holographic QCD predict for anomalous $(g-2)_\mu$?, 2015 (pdf)

• Josef Leutgeb, Anton Rebhan, Axial vector transition form factors in holographic QCD and their contribution to the anomalous magnetic moment of the muon (arXiv:1912.01596)

• Josef Leutgeb, Anton Rebhan, Axial vector transition form factors in holographic QCD and their contribution to the muon $g-2$ (arXiv:2012.06514)

• Josef Leutgeb, Anton Rebhan, Hadronic light-by-light contribution to the muon $g-2$ from holographic QCD with massive pions (arXiv:2108.12345)

• Josef Leutgeb, Jonas Mager, Anton Rebhan, Holographic QCD and the muon anomalous magnetic moment (arXiv:2110.07458)

Gravity contributions

Corrections at 1-loop from quantum gravity are discussed in

• F. A. Berends, R. Gastmans, Quantum gravity and the electron and muon anomalous magnetic moment, Phys. Lett. B55 Issue 3 Feb 1975 311-312 (doi:10.1016/0370-2693(75)90608-5)

This discussion is adapted to supergravity in

• F. del Aguila, A. Culatti, R. Munoz-Tapia, M. Perez-Victoria, Supergravity corrections to $(g-2)_l$ in differential renormalization, Nuclear Physics B 504 (1997) 532-550 (arXiv:hep-ph/9702342)

Axion contributions

Contribution of hypothetical axions to the anomalous magnetic moment of the electron and muon in QED:

• Yannis Semertzidis, Magnetic and Electric Dipole Moments in Storage Rings, chapter 6 of Markus Kuster, Georg Raffelt, Berta Beltrán (eds.), Axions: Theory, cosmology, and Experimental Searches, Lect. Notes Phys. 741 (Springer, Berlin Heidelberg 2008) (doi:10.1007/978-3-540-73518-2_2)

• Roberta Armillis, Claudio Coriano, Marco Guzzi, Simone Morelli, Axions and Anomaly-Mediated Interactions: The Green-Schwarz and Wess-Zumino Vertices at Higher Orders and g-2 of the muon, JHEP 0810:034,2008 (arXiv:0808.1882)

• W.J. Marciano, A. Masiero, P. Paradisi, M. Passera, Contributions of axion-like particles to lepton dipole moments, Phys. Rev. D 94, 115033 (2016) (arXiv:1607.01022)

• Martin Bauer, Matthias Neubert, Andrea Thamm, Collider Probes of Axion-Like Particles, J. High Energ. Phys. (2017) 2017: 44. (arXiv:1708.00443, doi:10.1007/JHEP12(2017)044)

The basic relevant Feynman diagrams are worked out here:

• pdf