nLab CW-pair

Idea

In algebraic topology, by a CW-pair $(X,A)$ is meant a CW-complex $X$ equipped with a sub-complex inclusion $A \hookrightarrow X$.

The concept appears prominently in the discussion of ordinary relative homology and generally in the Eilenberg-Steenrod axioms for generalized homology/generalized cohomology.

Properties

General

Proposition

For $X$ a CW complex, the inclusion $A \hookrightarrow X$ of any subcomplex has an open neighbourhood in $X$ which is a deformation retract of $A$. In particular such an inclusion is a good pair in the sense of relative homology.

For instance (Hatcher 2002, prop. A.5).

Proposition

For $(X,A)$ a CW-pair, then the $A$-relative singular homology of $X$ coincides with the reduced singular homology of the quotient space $X/A$:

$$H_n(X , A) \simeq \tilde H_n(X/A) \,.$$

For instance (Hatcher 2002, prop. 2.22).

Proof

By assumption we can find a neighbourhood $A \stackrel{j}{\to} U \hookrightarrow X$ such that $A \hookrightarrow U$ has a deformation retract and hence in particular is a homotopy equivalence and so induces also isomorphisms on all singular homology groups.

It follows in particular that for all $n \in \mathbb{N}$ the canonical morphism $H_n(X,A) \stackrel{H_n(id,j)}{\to} H_n(X,U)$ is an isomorphism, by homotopy invariance of relative singular homology.

Given such $U$ we have an evident commuting diagram of pairs of topological spaces

Here the right vertical morphism is in fact a homeomorphism.

Applying relative singular homology to this diagram yields for each $n \in \mathbb{N}$ the commuting diagram of abelian groups

Here the left horizontal morphisms are the above isomorphims induced from the deformation retract. The right horizontal morphisms are isomorphisms by excision and the right vertical morphism is an isomorphism since it is induced by a homeomorphism. Hence the left vertical morphism is an isomorphism (2-out-of-3 for isomorphisms).

Collapsing contractible subcomplexes

Proposition

If the sub-complex $A$ is contractible, then the quotient coprojection is a homotopy equivalence.

$$\ast \overset{\sim}{\longrightarrow} A \phantom{---} \Rightarrow \phantom{---} X \overset{\sim}{\longrightarrow} X/A \,.$$

(e.g. Hatcher p 11).

Example

Let $X$ be the pushout (in Top) which attaches an arc — identified as $A \subset X$ — to the 2-sphere, connecting a pair of distinct points:

(from Hatcher 2002)

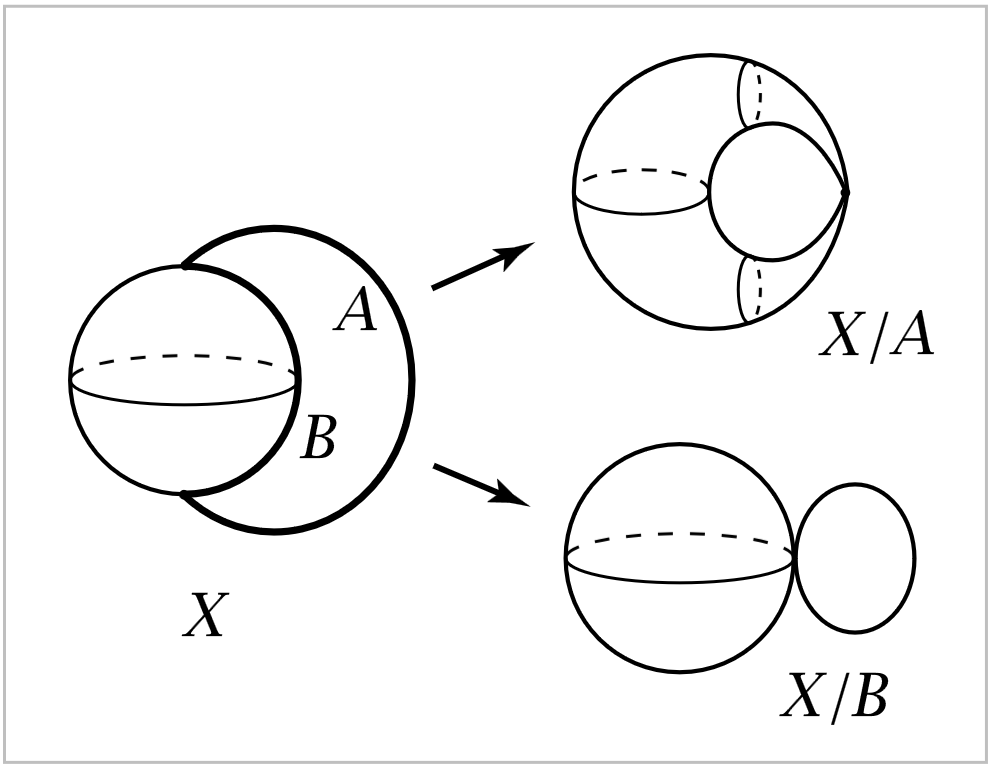
and let $B$ be any arc inside $S^2$ connecting these two distinct points. Then Prop. gives homotopy equivalences

$$S^2 / S^0 \,=\, X/A \overset{\sim}{\longrightarrow} X \overset{\sim}{\longrightarrow} X/B \,=\, S^2 \vee S^1 \,.$$

(e.g. Hatcher 2002 p 11).

In generalization of this example:

Example

For $\Sigma^2_{g,n} \,\coloneqq\, \Sigma^2_g \setminus \{s_1, \cdots, s_n\}$ the result of subjecting a closed surface $\Sigma^2_g$ to $n \geq 2$ punctures, the one-point compactification $\big(\Sigma^2_{g,n}\big)^\ast$ is homotopy equivalent to the wedge sum of the original surface with $n-1$ circles:

$$\big(\Sigma^2_{g,n}\big)^\ast \;\simeq\; \Sigma^2_g \,\vee\, \textstyle{\bigvee_{n-1}} S^1 \,.$$

This follows from Prop. by generalizing Ex. as follows: Instead of a single arc, take $A$ and $B$ there to each be, in themselves, the linear graph consisting of $n-1$ arcs (edges) and observe that that after identifying the vertices all with each other, this gives the wedge sum of $(n-1)$ circles.

Then take $X \coloneqq \Sigma^2_g \cup A$ to be the result of attaching this graph to the closed surface by gluing the vertices to the marked points (the would-be punctures) and observe that $(\Sigma^2_{g,n})^\ast = X/A$. With $B$ similarly identified as the corresponding graph but now embedded inside $\Sigma^2_g$, we have $X/B = \Sigma^2_g \,\vee\, \textstyle{\bigvee_{n-1}} S^1$.

References

• Allen Hatcher, Algebraic Topology, Cambridge University Press (2002) [ISBN:9780521795401, webpage]

• Marcelo Aguilar, Samuel Gitler, Carlos Prieto, section 5.1 of Algebraic topology from a homotopical viewpoint, Springer (2002) (toc pdf)