nLab Hanany-Witten effect
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
Idea
In string theory, what has come to be known as the Hanany-Witten-effect (or -process, -tansition, or -move) is an expected phenomenon exhibited by branes in type II string theory which is roughly described as follows:
“Moving an NS5-brane across a -brane creates a -brane stretching between the two”.
(Here in type IIA string theory and in type IIB string theory.)
Something like this was informally argued in Hanany & Witten (1997). Later authors have tried to offer explanation and illustration of what is meant to be happening here, as follows:
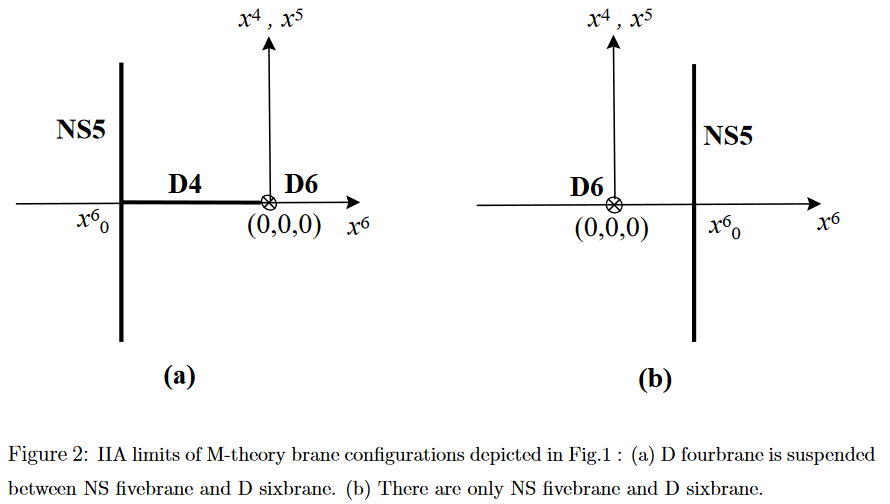
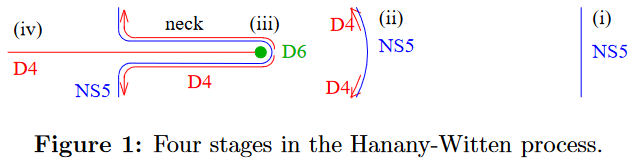
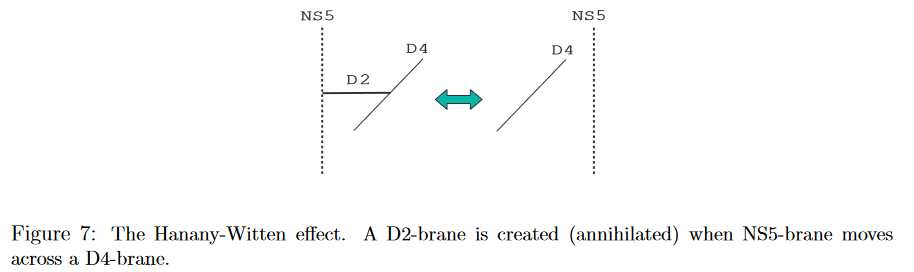
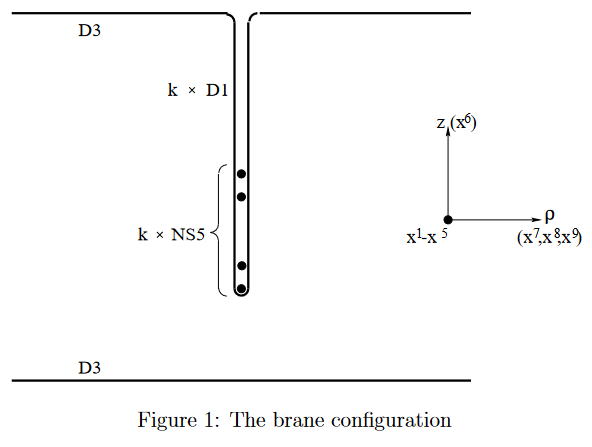
Marolf (2001) suggested that the Hanany-Witten effect may be understood entirely as a consequence of the famous (pregeometric) Bianchi identity for the RR-field-fluxes sourced by the D-branes, which is twisted by the B-field-flux sourced by NS5-branes:
and offered an argument in prose [Marolf (2001) pp. 3].
Below we spell out this approach in more detail.
Examples
D6 stretching between D8 and NS5
(cf. D6-D8 brane bound state and Bergshoeff, Lozano & Ortin (1998))
We explain the “Hanany-Witten effect” in detail for the case of “flat” NS5–D6–D8-configurations, as a consequence of the pregeometric Bianchi identities (1) satisfied by the flux densities sourced by these branes.
In this case we are dealing with
-
Minkowski spacetimes which we may identify with their canonical coordinate charts .
-
A closed differential 3-form
being the B-field flux density sourced by an NS5-brane with worldvolume
-
A closed differential 0-form (the “Romans mass”)
being the RR-field flux density sourced by a D8-brane whose worldvolume
we take to be located at for some .
-
being the RR-field flux density sourced by a D6-brane with potential worldvolume (“potential” because the D6 may have vanishing charge carried by parts of its worldvolume, hence may “disappear” from its would-be worldvolume locus in parts, as we will see):
(2)transverse to that of both the NS5-brane and the D8-brane and satisying the equation
(3)where now and are understood of the pullback (restriction) of the above differential forms of these names to the complement of the D6-brane worldvolume (2).
Notice that even if/though the original forms is not exact, after this pullback/restriction to this it does become exact, so that the equation (3) is meaningful.
In order to model the Hanany-Witten effect proper as considered by previous authors, we declare the following boundary conditions:
-
The Romans vacuum is to the “right” of the D8-brane
(4)Notice that the Bianchi identity for is , which means that it is a locally constant function whose jump across the D8-brane worldvolume measures the charge/number of these D8-branes (cf. eg. Fazzi (2017) p. 40). Hence
(5) -
There is no D6-brane to the far “left” of the NS5/D8,
(6)which just means to disregard D6-brane whose presence is not due to the Hanany-Witten effect.
With these boundary conditions set, the differential equation (3) may be solved for , and hence for the density of D6-brane charge/number which is “created” by the Hanany-Witten effect: At given the number/charge of D6-branes seen is the integral of around the 2-sphere in
over . Now there are two cases:
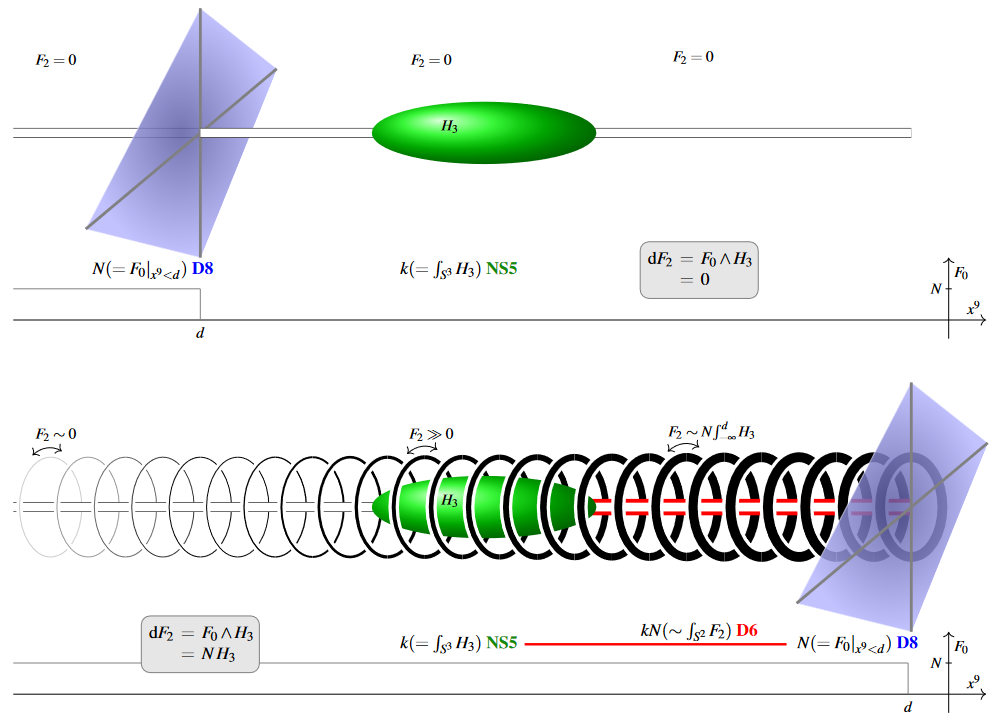
-
– indicated in the top part of figure (7)
In this case the NS5-brane is to the “right” of the D8-brane and hence in the Romans vacuum where . Here the differential equation (3) becomes
This means that does not change in the Romans vacuum, and hence if it vanishes to the left, as the boundary condition assumes, then it vanishes throughout.
Since the integral of counts the number/charge of D6-brane, the conclsusion is that no D6-branes are created in this situation.
-
– indicated in the bottom part of figure (7)
In this case the NS5-brane is to the “left” of the D8-brane and hence in the region where equals the number of D8-branes. Here the differential equation (3) becomes
This means now that as approach the NS5/D8-branes from the “left”, is continuously increasing by a rate measured by the density of NS5-brane flux. While this is everywhere non-vanishing, it is concentrated around the NS5-brane worldvolume locus (falling off by a power law from there). Therefore once we have “crossed the NS5-brane” and thus picked up most of its flux, will have increased from its asympotically vanishing value to , the product of the number of NS5-branes and D8-branes. This is hence the number of D6-branes “created” by the Hanany-Witten effect.
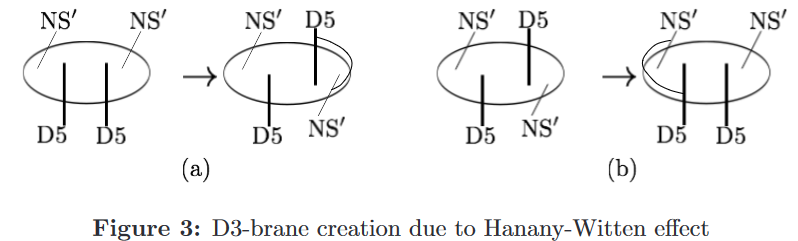
D3 stretching between D5 and NS5
(cf. D3-D5 brane bound state)
We discuss the “creation” of D3-brane flux “in between” a background of D5-brane- and NS5-brane flux as seen from (just) the pregeometric flux-equations.
If we assume that there are no D7-branes present in that the RR-field flux density which they source vanishes, , then the Bianchi identity for the D5-brane-flux is just
just as for the B-field flux density
Hence assume that there is a pair of flat parallel D5-branes and NS5-branes at a positive distance from each other
in that the respective flux densities are
and
In the following we regard both of these as further pulled back/restricted to the joint complement . Notice that as such they differ, one being the translate of the other by along one of the axes.
Now the Bianchi identity for the RR-field flux density sourced by any D3-branes is
Imposing the boundary condition that vanishes at infinity, the differential equation will imply the presence of non-vanishing -flux and hence of -branes “in between” the D5/NS5 iff the wedge product has the form of a “multipole” roughly supported in between these branes.
The following graphics, which shows a 2-dimensional shadow of the situation, qualitatively indicates that and why this is the case:
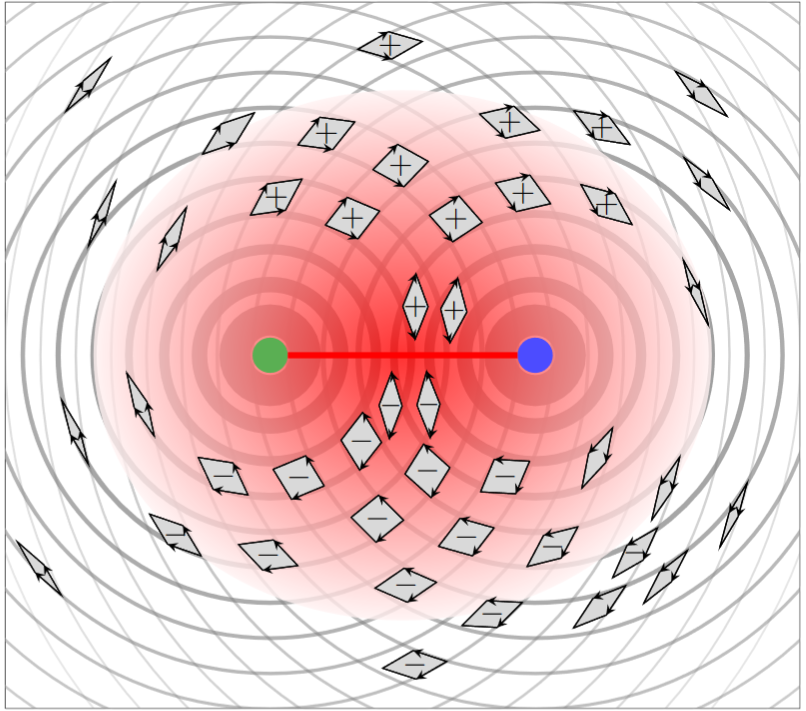
Here
-
the strength of the circular lines indicates the absolute value of the flux densities , (vanishing at infinity and spiked at the locus of the sourcing 5-brane),
-
the little arrows indicate the orientation? of the two flux densities, projected to the plane that is being shown
-
the little parallelograms indicate the orientation of the wedge product in the projection to the plane being shown.
(Hence what the graphics is really showing, approximately, is the wedge product of a pair of translates of pulled back to around either puncture of the 2-punctured plane.)
The point is to observe that — besides the abolute value of the wedge product evidently being concentrated near the branes, hence particularly between them when they are close — the sign of the orientation of the wedge product changes as the transverse coordinate passes through the axis between the branes.
Hence as we solve the differential equation incrementally by running, say, from the top to the bottom in the above graphics, we see that the absolute value of — indicated in above — fist incrementally picks up positive contributions as we approach the area between the branes, and then dimishies again as we leave that area. In total, the absolute value of the solution will be supported roughly in between the two 5-branes.
Since is the flux sourced by D3-branes, this means that D3-branes are seen to be “created” in between the 5-branes.
However, from this analysis of the fluxes alone, it does not follow that the D3-branes would disappear as the NS5- and D5-brane “swap positions”, as Hanany-Witten would suggest. In fact there is no intrinsic such directedness in the problem in the first place with respect to which one could even speak about the branes “swapping positions”.
Hence to see the full Hanany-Witten effect in this case, if it exists, one may have to look beyond the bare fluxes and include also the field of gravity. A suggestion for how this might work is given, for the analogous situation of M2-M5 brane intersections, in Hosomichi (2000), §5.
Related concepts
brane intersections/bound states/wrapped branes/polarized branes
-
D-branes and anti D-branes form bound states by tachyon condensation, thought to imply the classification of D-brane charge by K-theory
-
intersecting D-branes/fuzzy funnels:
-
Dp-D(p+6) brane bound state
References
The original article:
- Amihay Hanany, Edward Witten, Type IIB Superstrings, BPS Monopoles, And Three-Dimensional Gauge Dynamics, Nucl. Phys.B 492 (1997) 152-190 [arXiv:hep-th/9611230, doi:10.1016/S0550-3213(97)80030-2]
Further discussion:
-
Toshio Nakatsu, Kazutoshi Ohta, Takashi Yokono, Yuhsuke Yoshida, A Proof of Brane Creation via M theory, Mod. Phys. Lett. A 13 (1998) 293-302 [arXiv:hep-th/9711117, doi:10.1142/S0217732398000358]
-
Takahiro Kubota, Jian-Ge Zhou, RR charges of D2-branes in group manifold and Hanany-Witten effect, JHEP 0012 (2000) 030 [arXiv:hep-th/0010170, doi:10.1088/1126-6708/2000/12/030]
-
Donald Marolf, §2 of: T-duality and the case of the disappearing brane, JHEP 0106:036 (2001) [arXiv:hep-th/0103098, doi:10.1088/1126-6708/2001/06/036]
-
Minoru Eto, Youichi Isozumi, Muneto Nitta, Keisuke Ohashi, Kazutoshi Ohta, Norisuke Sakai, §3.3 in: D-brane Construction for Non-Abelian Walls, Phys.Rev. D 71 (2005) 125006 [arXiv:hep-th/0412024, doi:10.1103/PhysRevD.71.125006]
-
Oskar Pelc, , On the Quantization Constraints for a D3 Brane in the Geometry of NS5 Branes, JHEP 0008 (2000) 030 [arXiv:hep-th/0007100, doi:10.1088/1126-6708/2000/08/030]
-
Dongmin Gang, Eunkyung Koh, Kimyeong Lee, Jaemo Park, ABCD of 3d and 4 Superconformal Field Theories [arXiv:1108.3647]
See also:
- Wikipedia, Hanany-Witten transition
The case of D6-D8 brane bound states:
-
Amihay Hanany, Alberto Zaffaroni, §2.4 in: Chiral Symmetry from Type IIA Branes, Nucl. Phys. B 509 (1998) 145-168 [arXiv:hep-th/9706047, doi:10.1016/S0550-3213(97)00595-6]
-
Eric Bergshoeff, Yolanda Lozano, Tomas Ortin, p. 60 of: Massive Branes, Nucl. Phys. B 518 (1998) 363-423 [arXiv:hep-th/9712115, doi:10.1016/S0550-3213(98)00045-5]
Discussion for M2-M5 brane intersections:
- Kazuo Hosomichi, On Branes Ending on Branes in Supergravity, JHEP 0006 (2000) 004 [arXiv:hep-th/0002069, doi:10.1088/1126-6708/2000/06/004]
Last revised on January 27, 2024 at 16:58:28. See the history of this page for a list of all contributions to it.