nLab D6-brane

Idea

The D-brane of dimension 6+1 in type IIA string theory.

Relation to other branes

To the KK-monopole in M-theory

The lift of the D6 to M-theory is the Kaluza-Klein monopole there (Townsend 95).

One way to understand this is as follows: the first Chern class of the M-theory circle bundle is the D0-brane degree-2 RR-field strength $R_0$. By the self-duality of the RR-fields this is the Hodge dual of the D6-brane degree-8 field strength. Now given a Kaluza-Klein monopole after removing the locus of the monopole where the circle-fiber degenerates (as in the original Dirac charge quantization argument) it is a non-degenerated circle bundle such that the integral of the 2-form $R_0$ over any 2-sphere surrounding the singular locus is non-trivial. By the usual yoga of electric-magnetic duality this integral measures the magnetic flux of a D6-brane sitting at the singular locus. For more on this see at Kaluza-Klein monopole – Relation to the D6-brane, and see at M-theory lift of gauge enhancement on D6-branes.

To D7-branes

The T-dual of the D6 branes is the D7-brane in type IIB string theory.

Bound states

bound states/brane intersections involving D6-branes:

• D6-D8 brane bound state

• D2-D6 brane bound state

• D4-D6 brane bound state

Table of branes

from M-branes to F-branes: superstrings, D-branes and NS5-branes

M-theory on $S^1_A \times S^1_B$-elliptic fibration	KK-compactification on $S^1_A$	type IIA string theory	T-dual KK-compactification on $S^1_B$	type IIB string theory	geometrize the axio-dilaton	F-theory on elliptically fibered-K3 fibration	duality between F-theory and heterotic string theory	heterotic string theory on elliptic fibration
M2-brane wrapping $S_A^1$	double dimensional reduction $\mapsto$	type IIA superstring	$\mapsto$	type IIB superstring	$\mapsto$	“	$\mapsto$	heterotic superstring
M2-brane wrapping $S_B^1$	$\mapsto$	D2-brane	$\mapsto$	D1-brane	$\mapsto$	“
M2-brane wrapping $p$ times around $S_A^1$ and $q$ times around $S_B^1$	$\mapsto$	$p$ strings and $q$ D2-branes	$\mapsto$	(p,q)-string	$\mapsto$	“
M5-brane wrapping $S_A^1$	double dimensional reduction $\mapsto$	D4-brane	$\mapsto$	D5-brane	$\mapsto$	“
M5-brane wrapping $S_B^1$	$\mapsto$	NS5-brane	$\mapsto$	NS5-brane	$\mapsto$	“	$\mapsto$	NS5-brane
M5-brane wrapping $p$ times around $S_A^1$ and $q$ times around $S_B^1$	$\mapsto$	$p$ D4-brane and $q$ NS5-branes	$\mapsto$	(p,q)5-brane	$\mapsto$	“
M5-brane wrapping $S_A^1 \times S_B^1$	$\mapsto$		$\mapsto$	D3-brane	$\mapsto$	“
KK-monopole/A-type ADE singularity (degeneration locus of $S^1_A$-circle fibration, Sen limit of $S^1_A \times S^1_B$ elliptic fibration)	$\mapsto$	D6-brane	$\mapsto$	D7-branes	$\mapsto$	A-type nodal curve cycle degeneration locus of elliptic fibration (Sen 97, section 2)		SU-gauge enhancement
KK-monopole orientifold/D-type ADE singularity	$\mapsto$	D6-brane with O6-planes	$\mapsto$	D7-branes with O7-planes	$\mapsto$	D-type nodal curve cycle degeneration locus of elliptic fibration (Sen 97, section 3)		SO-gauge enhancement
exceptional ADE-singularity	$\mapsto$		$\mapsto$		$\mapsto$	exceptional ADE-singularity of elliptic fibration	$\mapsto$	E6-, E7-, E8-gauge enhancement

(e.g. Johnson 97, Blumenhagen 10)

Phenomenology – Intersecting D-brane models

D6-branes are the main ingredient in type IIA string phenomenology in the guise of intersecting D-brane models, see also at string phenomenology the section Models in type II with intersecting branes.

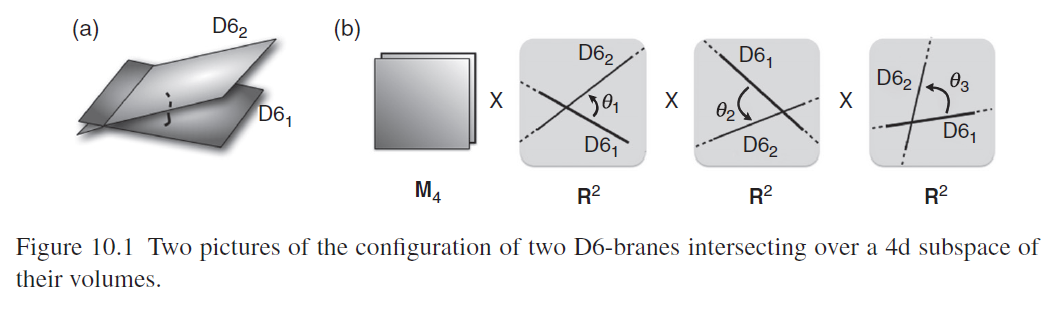
graphics grabbed from Ibáñez-Uranga 12

Related concept

Table of branes appearing in supergravity/string theory (for classification see at brane scan).

brane	in supergravity	charged under gauge field	has worldvolume theory
black brane	supergravity	higher gauge field	SCFT
D-brane	type II	RR-field	super Yang-Mills theory
$(D = 2n)$	type IIA	$\,$	$\,$
D(-2)-brane	$\,$	$\,$
D0-brane	$\,$	$\,$	BFSS matrix model
D2-brane	$\,$	$\,$	$\,$
D4-brane	$\,$	$\,$	D=5 super Yang-Mills theory with Khovanov homology observables
D6-brane	$\,$	$\,$	D=7 super Yang-Mills theory
D8-brane	$\,$	$\,$
$(D = 2n+1)$	type IIB	$\,$	$\,$
D(-1)-brane	$\,$	$\,$	$\,$
D1-brane	$\,$	$\,$	2d CFT with BH entropy
D3-brane	$\,$	$\,$	N=4 D=4 super Yang-Mills theory
D5-brane	$\,$	$\,$	$\,$
D7-brane	$\,$	$\,$	$\,$
D9-brane	$\,$	$\,$	$\,$
(p,q)-string	$\,$	$\,$	$\,$
(D25-brane)	(bosonic string theory)
NS-brane	type I, II, heterotic	circle n-connection	$\,$
string	$\,$	B2-field	2d SCFT
NS5-brane	$\,$	B6-field	little string theory
D-brane for topological string			$\,$
A-brane			$\,$
B-brane			$\,$
M-brane	11D SuGra/M-theory	circle n-connection	$\,$
M2-brane	$\,$	C3-field	ABJM theory, BLG model
M5-brane	$\,$	C6-field	6d (2,0)-superconformal QFT
M9-brane/O9-plane			heterotic string theory
M-wave
topological M2-brane	topological M-theory	C3-field on G₂-manifold
topological M5-brane	$\,$	C6-field on G₂-manifold
S-brane
SM2-brane, membrane instanton
M5-brane instanton
D3-brane instanton
solitons on M5-brane	6d (2,0)-superconformal QFT
self-dual string		self-dual B-field
3-brane in 6d

References

The relation to the Kaluza-Klein monopole in M-theory is due to

• Paul Townsend, The eleven-dimensional supermembrane revisited, Phys.Lett.B350:184-187,1995 (arXiv:hep-th/9501068)

Further discussion and derivation of the Chan-Paton gauge field content on the D6 from the KK-monopole is discussed in

• César Gómez, Juan José Manjarín, A note on the dyonic D6-brane, 6th International Workshop on Conformal Field Theory and Integrable Models, Landau Institute, Sept. 2002 (arXiv:hep-th/0302096)

• Juan José Manjarín, Topics on D-brane charges with B-fields, Int. J. Geom. Meth. Mod. Phys. 1 (2004) (arXiv:hep-th/0405074)

Discussion of D6 intersecting branes for intersecting D-brane models:

• Luis Ibáñez, Angel Uranga, String Theory and Particle Physics – An Introduction to String Phenomenology, Cambridge 2012

• Angel Uranga, Model building in IIA: Intersecting brane worlds, 2012 (pdf)