nLab E-string

Idea

In string theory, specifically in type IIA string theory, the brane intersection of a D2-brane with an O8-plane is called an E-string.

graphics grabbed from KKLPV 14, p. 4

Hence under the S-duality between type I and heterotic string theory the E-string is dual to the heterotic string.

The M-theory lift of the E-string is the brane intersection of an M2-brane with an M9-brane which wraps the M-theory circle fiber, hence an $M9_I$-brane of Horava-Witten theory (KKLPV 14, p. 4/5), hence a D8-brane from the dual perspective of type I' string theory.

The other end of the M2-brane-lift of the E-string is on an M5-brane:

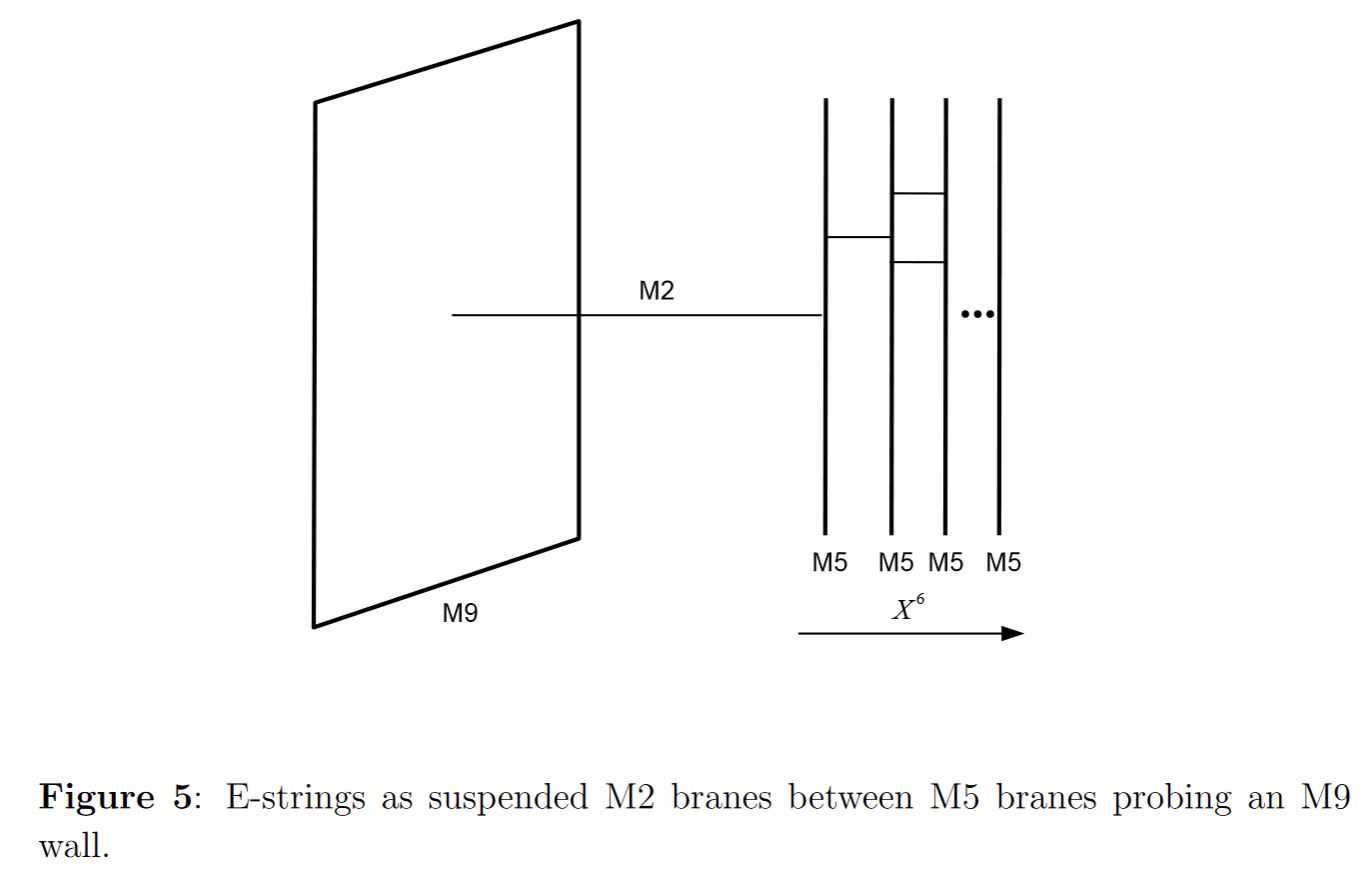
graphics grabbed from GHKKLV 15

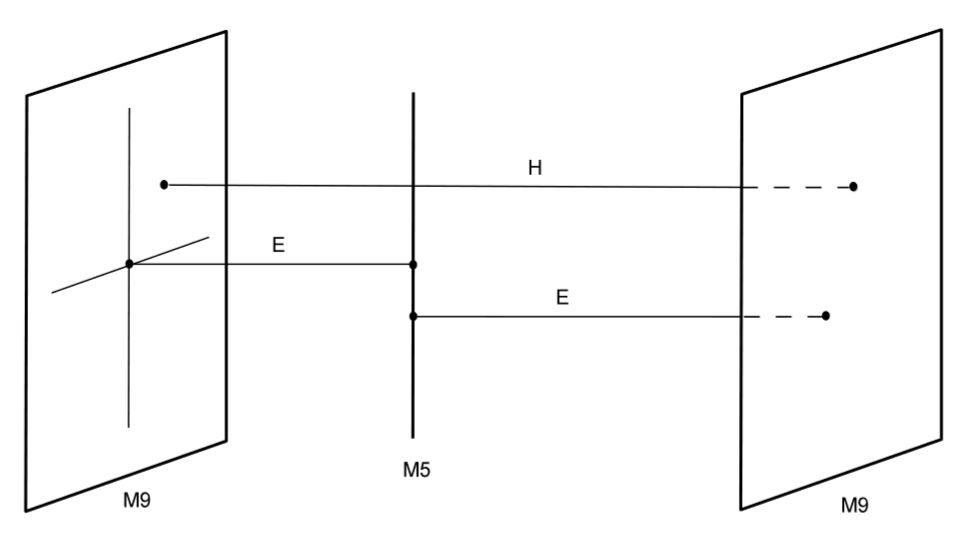
graphics grabbed from HLV 14

In contrast, if both ends of the M2-brane are on an M5-brane, some authors speak of “M-strings”:

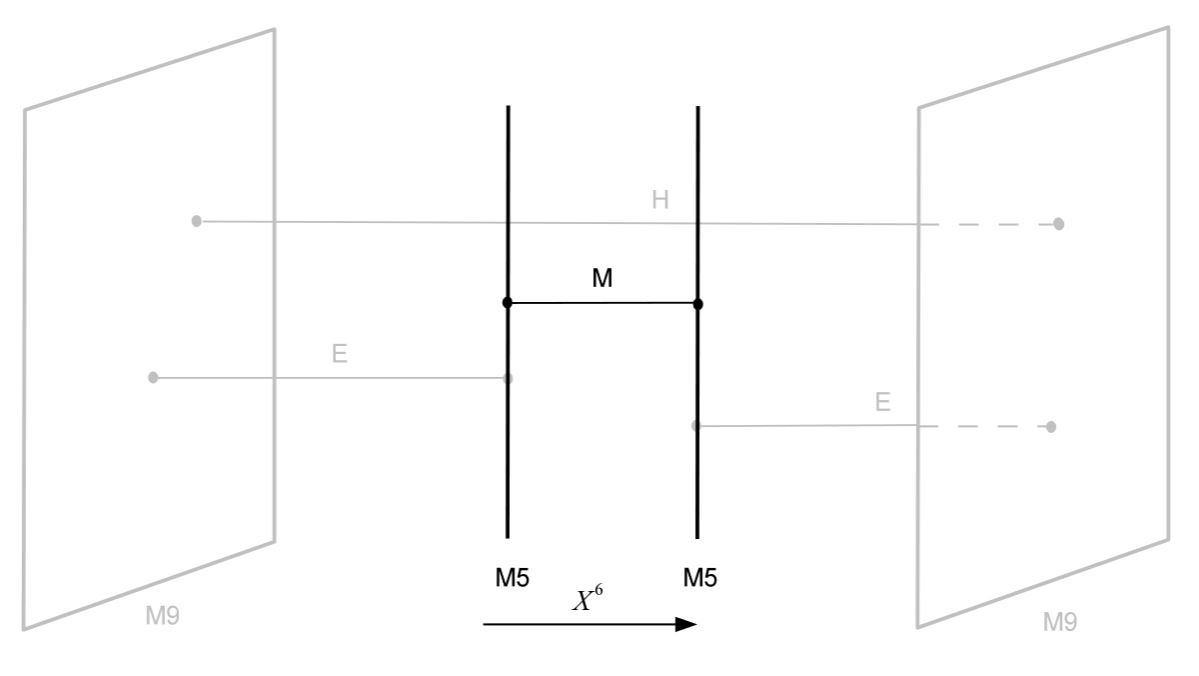
graphics grabbed from HLV 14

Finally, an M2-brane stretching between two MO9-planes gives the heterotic string at its boundary:

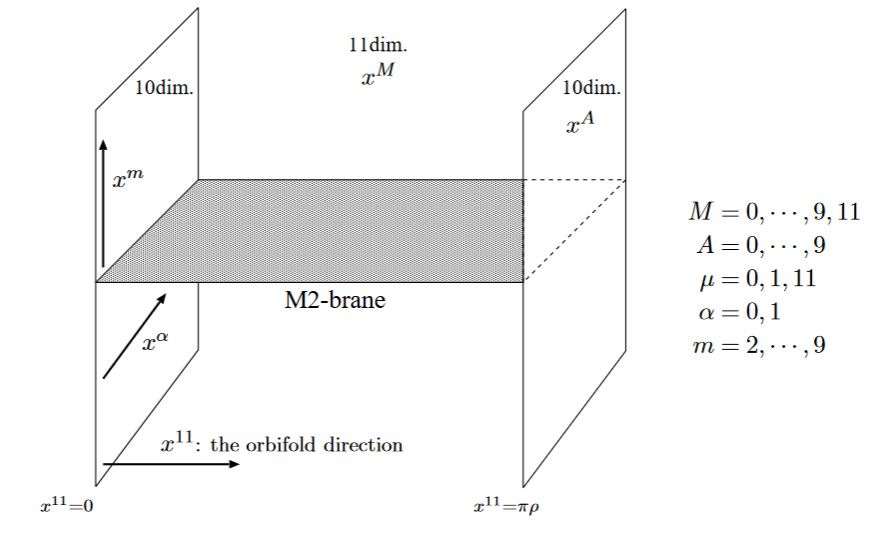
from Kashima 00

Properties

E-string elliptic genus

See at E-string elliptic genus.

Related concepts

• D=6 N=(1,0) SCFT

KK-compactification of M-theory

• M-theory on a circle

• M-theory on 8-manifolds/on Spin(7)-manifolds

• M-theory on G₂-manifolds

  • G₂-MSSM

• M-theory on Sp(1)-manifolds

• M-theory on hyperbolic manifolds

• heterotic M-theory on ADE-orbifolds

• M-theory on Calabi-Yau manifolds

  • on CY2-folds

  • on CY3-folds

  • on CY4-folds

  • on CY5-folds

brane intersections/bound states/wrapped branes/polarized branes

• D-branes and anti D-branes form bound states by tachyon condensation, thought to imply the classification of D-brane charge by K-theory

• intersecting D-branes/fuzzy funnels:

  • Dp-D(p+2)-brane bound state and Yang-Mills monopoles

    • D0-D2 brane bound state

    • D1-D3 brane bound state

    • D2-D4 brane bound state

    • D3-D5 brane bound state

    • D4-D6 brane bound state

    • D6-D8-brane bound state

  • Dp-D(p+4)-brane bound state and Yang-Mills instantons

    • D0-D4 brane bound state

    • D1-D5 brane bound state

    • D2-D6 brane bound state

    • D3-D7 brane bound state

    • D4-D8 brane bound state

    • D5-D9 brane bound state

      small instanton

• Dp-D(p+6) brane bound state

  • D0-D6 brane bound state

  • D1-D7 brane bound state

  • D2-D8 brane bound state

• NS5-D4-D2 bound states

• Hanany-Witten effect

S-duality$\,$bound states:

• (p,q)-string

• (p,q)5-branes

• string network

• 5-brane web

intersecting$\,$M-branes:

• M5-MO9 brane bound state

• M2-M5 brane bound state

  • M-string, E-string

• membrane triple junction

References

General

E-strings as M5-branes wrapped on a half K3?:

• J. A. Minahan, D. Nemeschansky, Nicholas Warner, Partition Functions for BPS States of the Non-Critical $E_8$ String, Adv. Theor. Math. Phys.1:167-183, 1998 (arXiv:hep-th/9707149)

• J. A. Minahan, D. Nemeschansky, Cumrun Vafa, Nicholas Warner, E-Strings and $N=4$ Topological Yang-Mills Theories, Nucl. Phys. B527 (1998) 581-623 (arXiv:hep-th/9802168)

• Amer Iqbal, A note on E-strings, Adv. Theor. Math. Phys. 7 (2003) 1-23 (arXiv:hep-th/0206064)

E-strings as M2-branes stretched between M5 and MO9:

• Babak Haghighat, Guglielmo Lockhart, Cumrun Vafa, Fusing E-string to heterotic string: $E + E \to H$, Phys. Rev. D 90 126012 (2014) [arXiv:1406.0850, doi:10.1103/PhysRevD.90.126012]

• Abhijit Gadde, Babak Haghighat, Joonho Kim, Seok Kim, Guglielmo Lockhart, Cumrun Vafa, 6d String Chains, JHEP 1802 (2018) 143 (arXiv:1504.04614)

On their Seiberg-Witten curve:

• Tohru Eguchi, Kazuhiro Sakai, Seiberg-Witten Curve for the E-String Theory, JHEP 0205:058, 2002 (arXiv:hep-th/0203025)

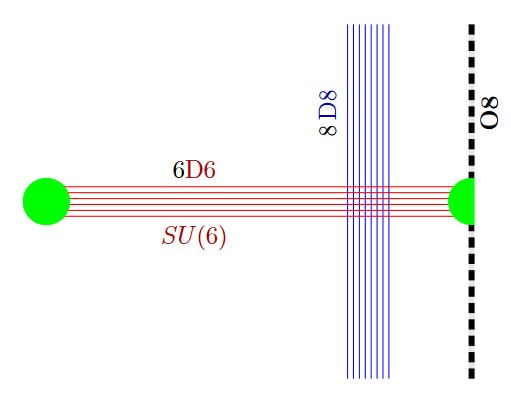
and on their quantum Seiberg-Witten curve in relation to D6-D8-brane bound states:

• Jin Chen, Babak Haghighat, Hee-Cheol Kim, Marcus Sperling, Xin Wang, E-string Quantum Curve, Nuclear Physics B 973 (2021) 115602 [arXiv:2103.16996, doi:10.1016/j.nuclphysb.2021.115602]

On the E-string elliptic genus:

• Kenji Mohri, Exceptional String: Instanton Expansions and Seiberg-Witten Curve, Rev. Math. Phys. 14 (2002) 913-975 (arXiv:hep-th/0110121)

• Joonho Kim, Seok Kim, Kimyeong Lee, Jaemo Park, Cumrun Vafa, Elliptic Genus of E-strings, JHEP 1709 (2017) 098 (arXiv:1411.2324)

• Wenhe Cai, Min-xin Huang, Kaiwen Sun, On the Elliptic Genus of Three E-strings and Heterotic Strings, J. High Energ. Phys. 2015, 79 (2015). (arXiv:1411.2801, doi:10.1007/JHEP01(2015)079)

On the Green-Schwarz anomaly cancellation in D=6 N=(1,0) SCFT:

• Kantaro Ohmori, Hiroyuki Shimizu, Yuji Tachikawa, Anomaly polynomial of E-string theories, J. High Energ. Phys. 2014, 2 (2014) (arXiv:1404.3887)

See also:

• Sung-Soo Kim, Yuji Sugimoto, Futoshi Yagi, Surface defects on E-string from 5-brane webs, JHEP 12(2020) 183 (arXiv:2008.06428)

In F-theory

Discussion in F-theory:

• Jie Gu, Babak Haghighat, Albrecht Klemm, Kaiwen Sun, Xin Wang, Elliptic Blowup Equations for 6d SCFTs. III: E–strings, M–strings and Chains (arXiv:1911.11724)

In heterotic M-theory on ADE-orbifolds

Discussion in heterotic M-theory on ADE-orbifolds, where the M5-branes parallel to an MO9 sit on an MK6/D6-brane on an ADE-singularity:

• E. Gorbatov, Vadim Kaplunovsky, Jacob Sonnenschein, Stefan Theisen, Shimon Yankielowicz, around (6.13) in On Heterotic Orbifolds, M Theory and Type I’ Brane Engineering, JHEP 0205:015, 2002 (arXiv:hep-th/0108135)

Relation to D$p$-D$(p+2)$-brane bound states

The lift of Dp-D(p+2)-brane bound states in string theory to M2-M5-brane bound states/E-strings in M-theory, under duality between M-theory and type IIA string theory+T-duality, via generalization of Nahm's equation (eventually motivating the BLG model/ABJM model):

• Anirban Basu, Jeffrey Harvey, The M2-M5 Brane System and a Generalized Nahm’s Equation, Nucl.Phys. B713 (2005) 136-150 (arXiv:hep-th/0412310)

• Jonathan Bagger, Neil Lambert, Sunil Mukhi, Constantinos Papageorgakis, Section 2.2.1 of Multiple Membranes in M-theory, Physics Reports, Volume 527, Issue 1, 1 June 2013, Pages 1-100 (arXiv:1203.3546, doi:10.1016/j.physrep.2013.01.006)