nLab twisted Pontrjagin theorem

Idea

A twisted Pontrjagin theorem should generalize the Pontrjagin theorem from plain homotopy theory/cobordism theory to parametrized homotopy theory/twisted cobordism theory:

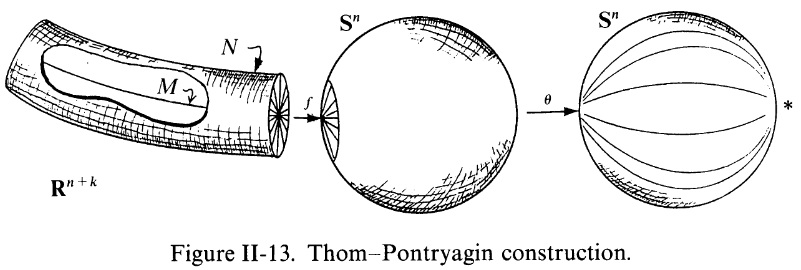
Where the plain Pontrjagin theorem identifies the Cohomotopy of a differentiable manifold with its cobordism classes of normally framed submanifolds, the twisted Pontrjagin theorem should identify twisted Cohomotopy with cobordism classes of normally twisted-framed submanifolds (Cruickshank 03, Lemma 5.2)

Related concepts

• Pontrjagin theorem, equivariant Pontrjagin theorem

References

Pontrjagin-Thom construction

Pontrjagin’s construction

General

The Pontryagin theorem, i.e. the unstable and framed version of the Pontrjagin-Thom construction, identifying cobordism classes of normally framed submanifolds with their Cohomotopy charge in unstable Borsuk-Spanier Cohomotopy sets, is due to:

• Lev Pontrjagin, Classification of continuous maps of a complex into a sphere, Communication I, Doklady Akademii Nauk SSSR 19 3 (1938) 147-149

• Lev Pontryagin, Homotopy classification of mappings of an (n+2)-dimensional sphere on an n-dimensional one, Doklady Akad. Nauk SSSR (N.S.) 19 (1950), 957–959 (pdf)

(both available in English translation in Gamkrelidze 86),

as presented more comprehensively in:

• Lev Pontrjagin, Smooth manifolds and their applications in Homotopy theory, Trudy Mat. Inst. im Steklov, No 45, Izdat. Akad. Nauk. USSR, Moscow, 1955 (AMS Translation Series 2, Vol. 11, 1959) (doi:10.1142/9789812772107_0001, pdf)

The Pontrjagin theorem must have been known to Pontrjagin at least by 1936, when he announced the computation of the second stem of homotopy groups of spheres:

• Lev Pontrjagin, Sur les transformations des sphères en sphères (pdf) in: Comptes Rendus du Congrès International des Mathématiques – Oslo 1936 (pdf)

Review:

• Daniel Freed, Karen Uhlenbeck, Appendix B of: Instantons and Four-Manifolds, Mathematical Sciences Research Institute Publications, Springer 1991 (doi:10.1007/978-1-4613-9703-8)

• Glen Bredon, chapter II.16 of: Topology and Geometry, Graduate Texts in Mathematics 139, Springer (1993) [doi:10.1007/978-1-4757-6848-0, pdf]

• Antoni Kosinski, chapter IX of: Differential manifolds, Academic Press (1993) [pdf, ISBN:978-0-12-421850-5]

• John Milnor, Chapter 7 of: Topology from the differentiable viewpoint, Princeton University Press, 1997. (ISBN:9780691048338, pdf)

• Mladen Bestvina (notes by Adam Keenan), Chapter 16 in: Differentiable Topology and Geometry, 2002 (pdf)

• Michel Kervaire, La méthode de Pontryagin pour la classification des applications sur une sphère, in: E. Vesentini (ed.), Topologia Differenziale, CIME Summer Schools, vol. 26, Springer 2011 (doi:10.1007/978-3-642-10988-1_3)

• Rustam Sadykov, Section 1 of: Elements of Surgery Theory, 2013 (pdf, pdf)

• András Csépai, Stable Pontryagin-Thom construction for proper maps, Period Math Hung 80, 259–268 (2020) (arXiv:1905.07734, doi:10.1007/s10998-020-00327-0)

Discussion of the early history:

• Kosinski 93, Section IX.9

Twisted/equivariant generalizations

The (fairly straightforward) generalization of the Pontrjagin theorem to the twisted Pontrjagin theorem, identifying twisted Cohomotopy with cobordism classes of normally twisted-framed submanifolds, is made explicit in:

• James Cruickshank, Lemma 5.2 using Sec. 5.1 in: Twisted homotopy theory and the geometric equivariant 1-stem, Topology and its Applications Volume 129, Issue 3, 1 April 2003, Pages 251-271 (doi:10.1016/S0166-8641(02)00183-9)

A general equivariant Pontrjagin theorem – relating equivariant Cohomotopy to normal equivariant framed submanifolds – remains elusive, but on free G-manifolds it is again straightforward (and reduces to the twisted Pontrjagin theorem on the quotient space), made explicit in:

• James Cruickshank, Thm. 5.0.6, Cor. 6.0.13 in: Twisted Cobordism and its Relationship to Equivariant Homotopy Theory, 1999 (pdf, pdf)

In negative codimension

In negative codimension, the Cohomotopy charge map from the Pontrjagin theorem gives the May-Segal theorem, now identifying Cohomotopy cocycle spaces with configuration spaces of points:

• Peter May, The geometry of iterated loop spaces, Springer 1972 (pdf)

• Graeme Segal, Configuration-spaces and iterated loop-spaces, Invent. Math. 21 (1973), 213–221. MR 0331377 (pdf)

  c Generalization of these constructions and results is due to

• Dusa McDuff, Configuration spaces of positive and negative particles, Topology Volume 14, Issue 1, March 1975, Pages 91-107 (doi:10.1016/0040-9383(75)90038-5)

• Carl-Friedrich Bödigheimer, Stable splittings of mapping spaces, Algebraic topology. Springer 1987. 174-187 (pdf, pdf)

Thom’s construction

Thom's theorem i.e. the unstable and oriented version of the Pontrjagin-Thom construction, identifying cobordism classes of normally oriented submanifolds with homotopy classes of maps to the universal special orthogonal Thom space $M SO(n)$, is due to:

• René Thom, Quelques propriétés globales des variétés différentiables, Comment. Math. Helv. 28, (1954). 17-86 (doi:10.1007/BF02566923, dml:139072, digiz:GDZPPN002056259, pdf)

Textbook accounts:

• Robert Stong, Notes on Cobordism theory, 1968 (toc pdf, publisher page)

Lashof’s construction

The joint generalization of Pontryagin 38a, 55 (framing structure) and Thom 54 (orientation structure) to any family of tangential structures (“(B,f)-structure”) is first made explicit in

• Richard Lashof, Poincaré duality and cobordism, Trans. AMS 109 (1963), 257-277 (doi:10.1090/S0002-9947-1963-0156357-4)

and the general statement that has come to be known as the Pontryagin-Thom isomorphism (identifying the stable cobordism classes of normally (B,f)-structured submanifolds with homotopy classes of maps to the Thom spectrum Mf) is really due to Lashof 63, Theorem C.

Textbook accounts:

• Theodor Bröcker, Tammo tom Dieck, Satz 3.1 & 4.9 in: Kobordismentheorie, Lecture Notes in Mathematics 178, Springer (1970) [ISBN:9783540053415]

• Stanley Kochman, section 1.5 of: Bordism, Stable Homotopy and Adams Spectral Sequences, AMS 1996

• Yuli Rudyak, On Thom spectra, orientability and cobordism, Springer Monographs in Mathematics (1998) [doi:10.1007/978-3-540-77751-9, pdf]

Lecture notes:

• John Francis, Topology of manifolds course notes (2010) (web), Lecture 3: Thom’s theorem (pdf), Lecture 4 Transversality (notes by I. Bobkova) (pdf)

• Cary Malkiewich, Section 3 of: Unoriented cobordism and $M O$, 2011 (pdf)

• Tom Weston, Part I of An introduction to cobordism theory (pdf)

See also:

• Manifold Atlas, The Pontrjagin-Thom isomorphism