nLab Thom's theorem
This entry is about Thom’s theorem in cobordism theory. For the isomorphism in cohomology induced by Thom classes see at Thom isomorphism.
Context
Cobordism theory
cobordism theory = manifolds and cobordisms + stable homotopy theory/higher category theory
Concepts of cobordism theory
-
homotopy classes of maps to Thom space MO
-
complex cobordism cohomology theory
flavors of bordism homology theories/cobordism cohomology theories, their representing Thom spectra and cobordism rings:
bordism theoryM(B,f) (B-bordism):
relative bordism theories:
global equivariant bordism theory:
algebraic:
Stable Homotopy theory
Ingredients
Contents
Contents
Idea
What is called Thom’s theorem or the Pontrjagin-Thom isomorphism (due to Thom 54, Pontrjagin 55) states that for a given universal tangential structure the stable homotopy groups of the universal Thom spectrum , with its canonical ring spectrum structure, form the cobordism ring
of manifolds with that tangential structure; and that this isomorphism is exhibited by the Pontryagin-Thom construction (see there).
More generally, for a topological space, the group of -bordism classes of -manifolds in is isomorphic to the generalized homology of with coefficients in :
Ingredients
Tangential structure on the Stable normal bundle
Definition
Given a smooth manifold of dimension and equipped with an embedding
for some , then the classifying map of its normal bundle is the function
which sends to the normal of the tangent space
regarded as a point in .
The normal bundle of itself is the subbundle of the tangent bundle
consisting of those vectors which are orthogonal to the tangent vectors of :
Definition
A (B,f)-structure is
-
for each a pointed CW-complex
-
equipped with a pointed Serre fibration
to the classifying space (def.);
-
for all a pointed continuous function
which is the identity for ;
such that for all these squares commute
where the bottom map is the canonical one from def. .
The -structure is multiplicative if it is moreover equipped with a system of maps which cover the canonical multiplication maps (def.)
and which satisfy the evident associativity and unitality, for the unit, and, finally, which commute with the maps in that all these squares commute:
and
Similarly, an --structure is a compatible system
indexed only on the even natural numbers.
Generally, an --structure for , is a compatible system
for all , hence for all .
We write for the universal vector bundle pulled back to the corresponding space of the -structure and with
and we write for the maps of total space of vector bundles over the :
Example
Examples of -structures (def. ) include the following:
-
and is orthogonal structure (or “no structure”);
-
and the universal principal bundle-projection is framing-structure;
-
the classifying space of the special orthogonal group and the canonical projection is orientation structure;
-
the classifying space of the spin group and the canonical projection is spin structure.
Examples of --structures (def. ) include
-
the classifying space of the unitary group, and the canonical projection is almost complex structure (or rather: almost Hermitian structure).
-
the classifying space of the symplectic group, and the canonical projection is almost symplectic structure.
Examples of --structures (def. ) include
- the classifying space of the quaternionic unitary group, and the canonical projection is almost quaternionic structure.
Definition
Given a smooth manifold of dimension , and given a -structure as in def. , then a -structure on the stable normal bundle of the manifold is an equivalence class of the following structure:
-
an embedding for some ;
-
a homotopy class of a lift of the classifying map of the normal bundle (def. )
The equivalence relation on such structures is to be that generated by the relation if
-
the second inclusion factors through the first as
-
the lift of the classifying map factors accordingly (as homotopy classes)
Bordism
Throughout, let be a multiplicative (B,f)-structure (def.).
Definition
Write for the standard interval, regarded as a smooth manifold with boundary. For Consider its embedding
as the arc
where denotes the canonical linear basis of , and equipped with the structure of a manifold with normal framing structure (def.) by equipping it with the canonical framing
of its normal bundle.
Let now be a (B,f)-structure (def.). Then for any embedded manifold with -structure on its normal bundle (def.), define its negative or orientation reversal of to be the restriction of the structured manifold
to .
Definition
Two closed manifolds of dimension equipped with normal -structure and (def.) are called bordant if there exists a manifold with boundary of dimension equipped with -strcuture if its boundary with -structure restricted to that boundary is the disjoint union of with the negative of , according to def.
Proposition
The relation of -bordism (def. ) is an equivalence relation.
Write for the -graded set of -bordism classes of -manifolds.
Proposition
Under disjoint union of manifolds, then the set of -bordism equivalence classes of def. becomes an -graded abelian group
(that happens to be concentrated in non-negative degrees). This is called the -bordism group.
Moreover, if the (B,f)-structure is multiplicative (def.), then Cartesian product of manifolds followed by the multiplicative composition operation of -structures makes the -bordism ring into a commutative ring, called the -bordism ring.
e.g. (Kochmann 96, prop. 1.5.3)
Thom spaces
Definition
Let be a topological space and let be a vector bundle over of rank , which is associated to an O(n)-principal bundle. Equivalently this means that is the pullback of the universal vector bundle (def. ) over the classifying space . Since preserves the metric on , by definition, such inherits the structure of a metric space-fiber bundle. With respect to this structure:
-
the unit disk bundle is the subbundle of elements of norm ;
-
the unit sphere bundle is the subbundle of elements of norm ;
;
-
the Thom space is the cofiber (formed in Top (prop.)) of
canonically regarded as a pointed topological space.
If is a general real vector bundle, then there exists an isomorphism to an -associated bundle and the Thom space of is, up to based homeomorphism, that of this orthogonal bundle.
Remark
If the rank of is positive, then is non-empty and then the Thom space (def. ) is the quotient topological space
However, in the degenerate case that the rank of vanishes, hence the case that , then , but . Hence now the pushout defining the cofiber is
which exhibits as the coproduct of with the point, hence as with a basepoint freely adjoined.
Proposition
Let be two real vector bundles. Then the Thom space (def. ) of the direct sum of vector bundles is expressed in terms of the Thom space of the pullbacks and of to the disk/sphere bundle of as
Proof
Notice that
-
;
-
.
(Since a point at radius in is a point of radius in and a point of radius in .)
Proposition
For a vector bundle then the Thom space (def. ) of , the direct sum of vector bundles with the trivial rank vector bundle, is homeomorphic to the smash product of the Thom space of with the -sphere (the -fold reduced suspension).
Example
By prop. and remark the Thom space (def. ) of a trivial vector bundle of rank is the -fold suspension of the base space
Therefore a general Thom space may be thought of as a “twisted suspension”, with twist encoded by a vector bundle (or rather by its underlying spherical fibration). See at Thom spectrum – For infinity-module bundles for more on this.
Proposition
For and to vector bundles, let be the direct sum of vector bundles of their pullbacks to . The corresponding Thom space (def. ) is the smash product of the individual Thom spaces:
Universal Thom spectra
Proposition
For each the pullback of the rank- universal vector bundle to the classifying space of rank vector bundles is the direct sum of vector bundles of the rank universal vector bundle with the trivial rank-1 bundle: there is a pullback diagram of topological spaces of the form
where the bottom morphism is the canonical one (def.).
(e.g. Kochmann 96, p. 25)
Proof
For each , there is such a pullback of the canonical vector bundles over Grassmannians
where the bottom morphism is the canonical inclusion (def.).
Now we claim that taking the colimit in each of the four corners of this system of pullback diagrams yields again a pullback diagram, and this proves the claim.
To see this, remember that we work in the category of compactly generated topological spaces (def.). By their nature, we may test the universal property of a would-be pullback space already by mapping compact topological spaces into it. Now observe that all the inclusion maps in the four corners of this system of diagrams are relative cell complex inclusions, by prop. . Together this implies (via this lemma) that we may test the universal property of the colimiting square at finite stages. And so this implies the claim by the above fact that at each finite stage there is a pullback diagram.
Definition
The universal real Thom spectrum is the spectrum, which is represented by the sequential prespectrum (def.) whose th component space is the Thom space (def. )
of the rank- universal vector bundle, and whose structure maps are the image under the Thom space functor of the top morphisms in prop. , via the homeomorphisms of prop. :
More generally, there are universal Thom spectra associated with any other tangent structure (“(B,f)-structure”), notably for the orthogonal group replaced by the special orthogonal groups , or the spin groups , or the string 2-group , or the fivebrane 6-group ,…, or any level in the Whitehead tower of . To any of these groups there corresponds a Thom spectrum (denoted, respectively, , MSpin, , , etc.), which is in turn related to oriented cobordism, spin cobordism, string cobordism, et cetera.:
Definition
Given a (B,f)-structure (def. ), write for the pullback of the universal vector bundle (def. ) to the corresponding space of the -structure and with
and we write for the maps of total space of vector bundles over the :
Observe that the analog of prop. still holds:
Proposiiton
Given a (B,f)-structure (def. ), then the pullback of its rank- vector bundle (def. ) along the map is the direct sum of vector bundles of the rank- bundle with the trivial rank-1-bundle: there is a pullback square
Proof
Unwinding the definitions, the pullback in question is
Definition
Given a (B,f)-structure (def. ), its universal Thom spectrum is, as a sequential prespectrum, given by component spaces being the Thom spaces (def. ) of the -associated vector bundles of def.
and with structure maps given via prop. by the top maps in prop. :
Similarly for an -structure indexed on every th natural number (such as almost complex structure, almost quaternionic structure, example ), there is the corresponding Thom spectrum as a sequential spectrum (def.).
If for some natural system of groups , then one usually writes for . For instance , MSpin, MU, MSp etc.
If the -structure is multiplicative (def. ), then the Thom spectrum canonical becomes a ring spectrum: the multiplication maps are covered by maps of vector bundles
and under forming Thom spaces this yields (prop.) maps
which are associative by the associativity condition in a multiplicative -structure. The unit is
Example
The universal Thom spectrum (def. ) for framing structure (exmpl.) is equivalently the sphere spectrum (def.)
Because in this case and so , whence .
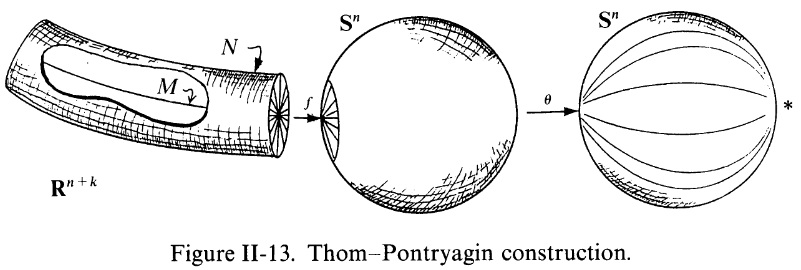
Pontrjagin-Thom construction
Definition
For a smooth manifold and an embedding, then a tubular neighbourhood of is a subset of the form
for some , , small enough such that the map
from the normal bundle (def. ) given by
is a diffeomorphism.
Proposition
(tubular neighbourhood theorem)
For every embedding of smooth manifolds, there exists a tubular neighbourhood according to def. .
Remark
Given an embedding with a tubuluar neighbourhood (def. ) then by construction:
-
the Thom space (def. ) of the normal bundle (def. ) is homeomorphic to the quotient topological space of the topological closure of the tubular neighbourhood by its boundary:
;
-
there exists a continous function
which is the identity on and is constant on the basepoint of the quotient on all other points.
Definition
For a smooth manifold of dimension and for an embedding, then the Pontrjagin-Thom collapse map is, for any choice of tubular neighbourhood (def. ) the composite map of pointed topological spaces
where the first map identifies the k-sphere as the one-point compactification of ; and where the second and third maps are those of remark .
The Pontrjagin-Thom construction is the further composite
with the image under the Thom space construction of the morphism of vector bundles
induced by the classifying map of the normal bundle (def. ).
This defines an element
in the th stable homotopy group (def.) of the Thom spectrum (def. ).
More generally, for a smooth manifold with normal (B,f)-structure according to def. , then its Pontrjagin-Thom construction is the composite
with
Proposition
The Pontrjagin-Thom construction (def. ) respects the equivalence classes entering the definition of manifolds with stable normal -structure (def. ) hence descends to a function (of sets)
Proof
It is clear that the homotopies of classifying maps of -structures that are devided out in def. map to homotopies of representatives of stable homotopy groups. What needs to be shown is that the construction respects the enlargement of the embedding spaces.
Given a embedded manifold with normal -structure
write
for its image under the Pontrjagin-Thom construction (def. ). Now given , consider the induced embedding with normal -structure given by the composite
By prop. and using the pasting law for pullbacks, the classifying map for the enlarged normal bundle sits in a diagram of the form
Hence the Pontrjagin-Thom construction for the enlarged embedding space is (using prop. ) the composite
The composite of the first two morphisms here is , while last morphism is the structure map in the Thom spectrum (by def. ):
This manifestly identifies as being the image of under the component map in the sequential colimit that defines the stable homotopy groups (def.). Therefore and , for all , represent the same element in .
Thom’s theorem
Recall that the Pontrjagin-Thom construction (def.) associates to an embbeded manifold with normal -structure (def.) an element in the stable homotopy group of the universal -Thom spectrum in degree the dimension of that manifold.
Lemma
For be a multiplicative (B,f)-structure (def.), the -Pontrjagin-Thom construction (def.) is compatible with all the relations involved to yield a graded ring homomorphism
from the -bordism ring (def. ) to the stable homotopy groups of the universal -Thom spectrum equipped with the ring structure induced from the canonical ring spectrum structure (def.).
Proof
By prop. the underlying function of sets is well-defined before dividing out the bordism relation (def. ). To descend this further to a function out of the set underlying the bordism ring, we need to see that the Pontrjagin-Thom construction respects the bordism relation. But the definition of bordism is just so as to exhibit under a left homotopy of representatives of homotopy groups.
Next we need to show that it is
-
a group homomorphism;
-
a ring homomorphism.
Regarding the first point:
The element 0 in the cobordism group is represented by the empty manifold. It is clear that the Pontrjagin-Thom construction takes this to the trivial stable homotopy now.
Given two -manifolds with -structure, we may consider an embedding of their disjoint union into some such that the tubular neighbourhoods of the two direct summands do not intersect. There is then a map from two copies of the k-cube, glued at one face
such that the first manifold with its tubular neighbourhood sits inside the image of the first cube, while the second manifold with its tubular neighbourhood sits indide the second cube. After applying the Pontryagin-Thom construction to this setup, each cube separately maps to the image under of the respective manifold, while the union of the two cubes manifestly maps to the sum of the resulting elements of homotopy groups, by the very definition of the group operation in the homotopy groups (def.). This shows that is a group homomorphism.
Regarding the second point:
The element 1 in the cobordism ring is represented by the manifold which is the point. Without restriction we may consoder this as embedded into , by the identity map. The corresponding normal bundle is of rank 0 and hence (by remark ) its Thom space is , the 0-sphere. Also is the rank-0 vector bundle over the point, and hence (by def. ) and so indeed represents the unit element in .
Finally regarding respect for the ring product structure: for two manifolds with stable normal -structure, represented by embeddings into , then the normal bundle of the embedding of their Cartesian product is the direct sum of vector bundles of the separate normal bundles bulled back to the product manifold. In the notation of prop. there is a diagram of the form
To the Pontrjagin-Thom construction of the product manifold is by definition the top composite in the diagram
which hence is equivalently the bottom composite, which in turn manifestly represents the product of the separate PT constructions in .
Theorem
The ring homomorphsim in lemma is an isomorphism.
Due to (Thom 54, Pontrjagin 55). See for instance (Kochmann 96, theorem 1.5.10).
Proof idea
Observe that given the result of the Pontrjagin-Thom construction map, the original manifold may be recovered as this pullback:
To see this more explicitly, break it up into pieces:
Moreover, since the n-spheres are compact topological spaces, and since the classifying space , and hence its universal Thom space, is a sequential colimit over relative cell complex inclusions, the right vertical map factors through some finite stage (by this lemma), the manifold is equivalently recovered as a pullback of the form
(Recall that is our notation for the universal vector bundle with -structure, while denotes a Stiefel manifold.)
The idea of the proof now is to use this property as the blueprint of the construction of an inverse to : given an element in represented by a map as on the right of the above diagram, try to define and the structure map of its normal bundle as the pullback on the left.
The technical problem to be overcome is that for a general continuous function as on the right, the pullback has no reason to be a smooth manifold, and for two reasons:
-
the map may not be smooth around the image of ;
-
even if it is smooth around the image of , it may not be transversal to , and the intersection of two non-transversal smooth functions is in general still not a smooth manifold.
The heart of the proof is in showing that for any there are small homotopies relating it to an that is both smooth around the image of and transversal to .
The first condition is guaranteed by Sard's theorem, the second by Thom's transversality theorem.
(…)
Related entries
References
Pontrjagin-Thom construction
Pontrjagin’s construction
General
The Pontryagin theorem, i.e. the unstable and framed version of the Pontrjagin-Thom construction, identifying cobordism classes of normally framed submanifolds with their Cohomotopy charge in unstable Borsuk-Spanier Cohomotopy sets, is due to:
-
Lev Pontrjagin, Classification of continuous maps of a complex into a sphere, Communication I, Doklady Akademii Nauk SSSR 19 3 (1938) 147-149
-
Lev Pontryagin, Homotopy classification of mappings of an (n+2)-dimensional sphere on an n-dimensional one, Doklady Akad. Nauk SSSR (N.S.) 19 (1950), 957–959 (pdf)
(both available in English translation in Gamkrelidze 86),
as presented more comprehensively in:
- Lev Pontrjagin: Smooth manifolds and their applications in Homotopy theory, Trudy Mat. Inst. im Steklov 45 Izdat. Akad. Nauk. USSR, Moscow (1955), AMS Translation Series 2 11 (1959) doi:10.1142/9789812772107_0001, pdf]
The Pontrjagin theorem must have been known to Pontrjagin at least by 1936, when he announced the computation of the second stem of homotopy groups of spheres:
- Lev Pontrjagin, Sur les transformations des sphères en sphères (pdf) in: Comptes Rendus du Congrès International des Mathématiques – Oslo 1936 (pdf)
Review:
-
Daniel Freed, Karen Uhlenbeck, Appendix B of: Instantons and Four-Manifolds, Mathematical Sciences Research Institute Publications, Springer 1991 (doi:10.1007/978-1-4613-9703-8)
-
Glen Bredon, chapter II.16 of: Topology and Geometry, Graduate Texts in Mathematics 139, Springer (1993) [doi:10.1007/978-1-4757-6848-0, pdf]
-
Antoni Kosinski, chapter IX of: Differential manifolds, Academic Press (1993) [pdf, ISBN:978-0-12-421850-5]
-
John Milnor, Chapter 7 of: Topology from the differentiable viewpoint, Princeton University Press (1997) ISBN:9780691048338, pdf]
-
Mladen Bestvina (notes by Adam Keenan), Chapter 16 in: Differentiable Topology and Geometry (2002) pdf]
-
Michel Kervaire, La méthode de Pontryagin pour la classification des applications sur une sphère, in: E. Vesentini (ed.), Topologia Differenziale, CIME Summer Schools, vol. 26, Springer 2011 (doi:10.1007/978-3-642-10988-1_3)
-
Rustam Sadykov, Section 1 of: Elements of Surgery Theory, 2013 (pdf, pdf)
-
Riccardo Benedetti, chapter 17 of: Lectures on Differential Topology, Graduate Studies in Mathematics 218, AMS (2021) [arXiv:1907.10297, ISBN: 978-1-4704-6674-9]
-
András Csépai, Stable Pontryagin-Thom construction for proper maps, Period Math Hung 80, 259–268 (2020) (arXiv:1905.07734, doi:10.1007/s10998-020-00327-0)
See also further references at differential topology.
Discussion of the early history:
Twisted/equivariant generalizations
The (fairly straightforward) generalization of the Pontrjagin theorem to the twisted Pontrjagin theorem, identifying twisted Cohomotopy with cobordism classes of normally twisted-framed submanifolds, is made explicit in:
- James Cruickshank, Lemma 5.2 using Sec. 5.1 in: Twisted homotopy theory and the geometric equivariant 1-stem, Topology and its Applications Volume 129, Issue 3, 1 April 2003, Pages 251-271 (doi:10.1016/S0166-8641(02)00183-9)
A general equivariant Pontrjagin theorem – relating equivariant Cohomotopy to normal equivariant framed submanifolds – remains elusive, but on free G-manifolds it is again straightforward (and reduces to the twisted Pontrjagin theorem on the quotient space), made explicit in:
- James Cruickshank, Thm. 5.0.6, Cor. 6.0.13 in: Twisted Cobordism and its Relationship to Equivariant Homotopy Theory, 1999 (pdf, pdf)
In negative codimension
In negative codimension, the Cohomotopy charge map from the Pontrjagin theorem gives the May-Segal theorem, now identifying Cohomotopy cocycle spaces with configuration spaces of points:
-
Peter May, The geometry of iterated loop spaces, Springer 1972 (pdf)
-
Graeme Segal, Configuration-spaces and iterated loop-spaces, Invent. Math. 21 (1973), 213–221. MR 0331377 (pdf)
c Generalization of these constructions and results is due to
-
Dusa McDuff, Configuration spaces of positive and negative particles, Topology Volume 14, Issue 1, March 1975, Pages 91-107 (doi:10.1016/0040-9383(75)90038-5)
-
Carl-Friedrich Bödigheimer, Stable splittings of mapping spaces, Algebraic topology. Springer 1987. 174-187 (pdf, pdf)
Thom’s construction
Thom's theorem i.e. the unstable and oriented version of the Pontrjagin-Thom construction, identifying cobordism classes of normally oriented submanifolds with homotopy classes of maps to the universal special orthogonal Thom space , is due to:
- René Thom, Quelques propriétés globales des variétés différentiables, Comment. Math. Helv. 28, (1954). 17-86 (doi:10.1007/BF02566923, dml:139072, digiz:GDZPPN002056259, pdf)
Textbook accounts:
- Robert Stong: Notes on Cobordism theory, (1968) toc pdf, publisher page]
Lashof’s construction
The joint generalization of Pontryagin 38a, 55 (framing structure) and Thom 54 (orientation structure) to any family of tangential structures (“(B,f)-structure”) is first made explicit in
- Richard Lashof, Poincaré duality and cobordism, Trans. AMS 109 (1963), 257-277 (doi:10.1090/S0002-9947-1963-0156357-4)
and the general statement that has come to be known as the Pontryagin-Thom isomorphism (identifying the stable cobordism classes of normally (B,f)-structured submanifolds with homotopy classes of maps to the Thom spectrum Mf) is really due to Lashof 63, Theorem C.
Textbook accounts:
-
Theodor Bröcker, Tammo tom Dieck, Satz 3.1 & 4.9 in: Kobordismentheorie, Lecture Notes in Mathematics 178, Springer (1970) [ISBN:9783540053415]
-
Stanley Kochman, section 1.5 of: Bordism, Stable Homotopy and Adams Spectral Sequences, AMS 1996
-
Yuli Rudyak, On Thom spectra, orientability and cobordism, Springer Monographs in Mathematics (1998) [doi:10.1007/978-3-540-77751-9, pdf]
Lecture notes:
-
John Francis, Topology of manifolds course notes (2010) (web), Lecture 3: Thom’s theorem (pdf), Lecture 4 Transversality (notes by I. Bobkova) (pdf)
-
Cary Malkiewich, Section 3 of: Unoriented cobordism and , 2011 (pdf)
-
Tom Weston, Part I of An introduction to cobordism theory (pdf)
See also:
Last revised on March 4, 2024 at 23:27:33. See the history of this page for a list of all contributions to it.