nLab superconductivity

Skip the Navigation Links | Home Page | All Pages | Latest Revisions | Discuss this page |
Redirected from "Meissner effect".
Contents

Context

Solid state physics

Contents

Idea

(…)

Properties

Magnetic flux quantization in type II superconductors

Due to the Meissner-Ochsenfeld effect, a superconductor placed in a sufficiently small external magnetic field H ext<H c 1H_{ext} \lt H_{c_1} (aligned along some axis) “expels” that field , making the total magnetic field in the bulk of the superconductor vanish. However, as the ambient magnetic field exceeds a critical value H c 1H_{c_1}, this behaviour changes:

  • for type I superconductors, the superconducting state simply breaks down as H ext>H c 1H_{ext} \gt H_{c_1} and the ambient magnetic field fully penetrates the material as for any normal conductor;

  • for type II superconductors the superconducting state eventually also breaks down as H ext>H c 2>H c 1H_{ext} \gt H_{c_2} \gt H_{c_1}, but there is an intermediate parameter region H c 1<H ext<H c 2H_{c_1} \lt H_{ext} \lt H_{c_2} where both regimes mix:

From Chapman 09

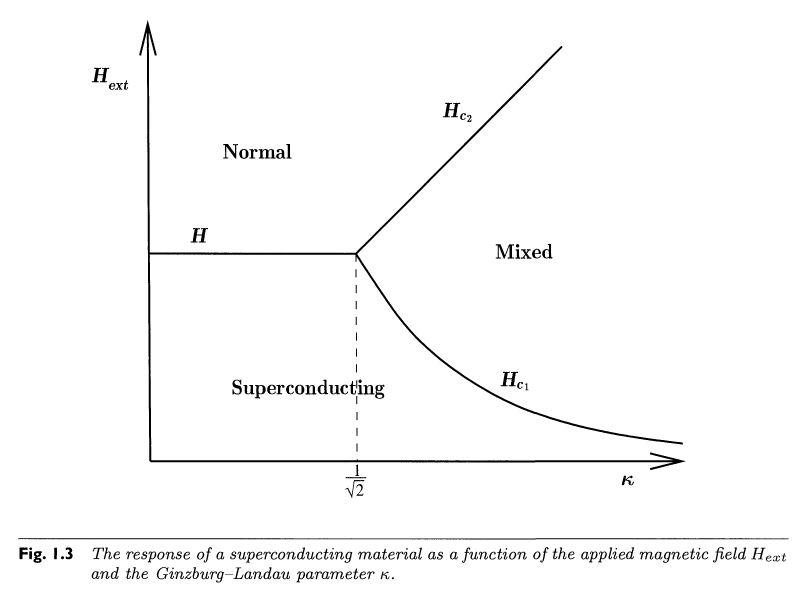
In this mixed regime, a finite number of elementary units of magnetic flux enter the superconductor, carried by little flux tubes inside vortices of electric currents: vortex strings (about a micron in diameter, e.g. Chapman 00, p. 559). Each vortex core carries one unit of magnetic flux – also called a fluxon – while at some small finite distance away from all vortices, the bulk magnetic flux in the superconductor still vanishes (mathematically: it vanishes at infinity, cf. eg. Chapman 2009 (2.31), Timm 2020 (6.101)) :

(1)
adapted from Loudon and Midgley 2009

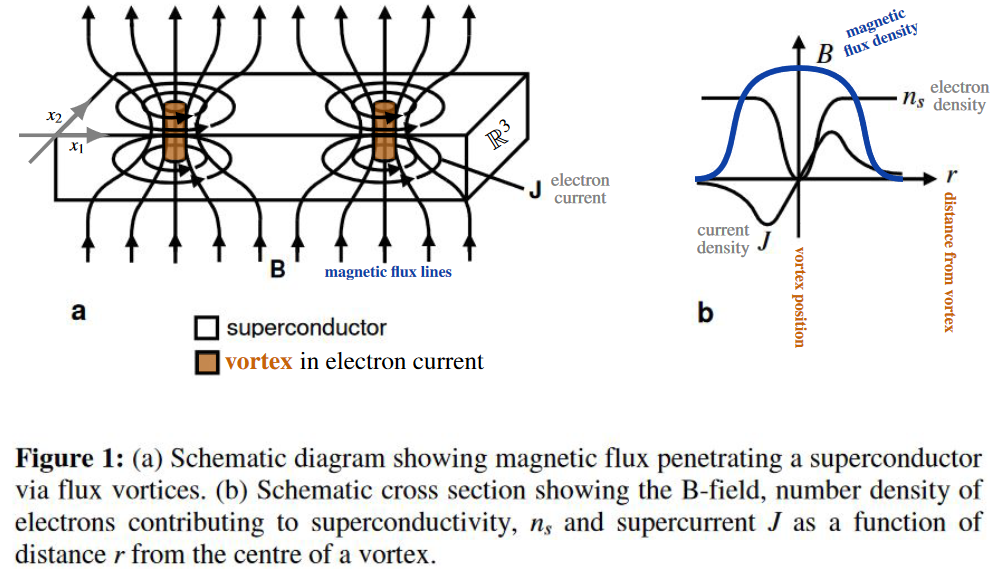
At sufficiently large density these vortices arrange into hexagonal patterns, first described by Abrikosov 57, whence also known as Abrikosov vortices.

(2)
from Yu 2012

This flux quantization in type II superconductors is traditionally explained via the effective field theory provided by the Landau-Ginzburg model; the derivation may be found reviewed in Chapman 00 (Section 2, culminating in (2.33)).

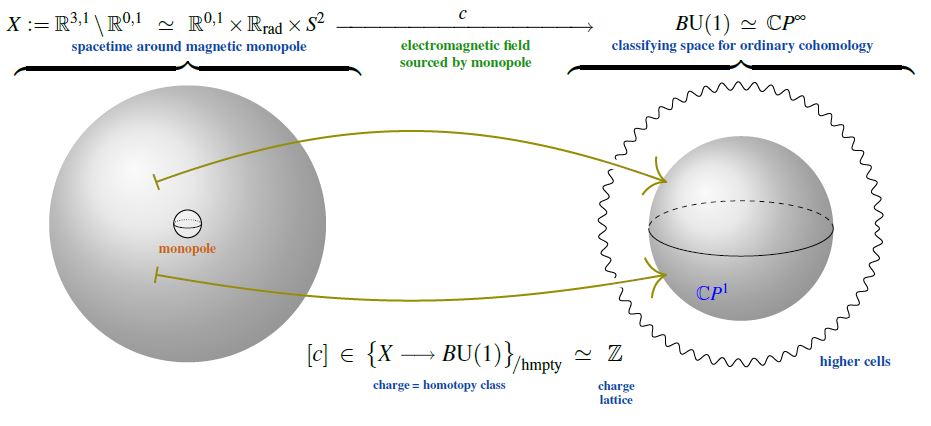
But, as indicated a little more explicitly in Alvarez-Gaumé 98 (Section IV.B, culminating below IV.11), the flux quantization as such is mathematically a direct consequence of the global topological nature of the electromagnetic field, the argument being the direct 2-dimensional analog of the quantization of instantons in QCD in 4d (see also at SU(2)-Instantons – From the correct maths to the traditional physics story) and in fact is but a slight variation of the argument for Dirac charge quantization of magnetic monopoles:

Namely, the electromagnetic field is a connection on a circle bundle, and hence the cohomology classifying space for the topological class of the electromagnetic field is the classifying space B U ( 1 ) B \mathrm{U}(1) of the circle group, which, being an Eilenberg-MacLane space K(ℤ,2)K(\mathbb{Z},2), has second homotopy group the integers:

π 2(BU(1))≃{S 2→BU(1)} /hmpty≃ℤ. \pi_2(B \mathrm{U}(1)) \;\simeq\; \big\{ S^2 \to B \mathrm{U}(1)\big\}_{\big/hmpty} \;\simeq\; \mathbb{Z} \,.

This implies that on every spacetime which looks, up to homotopy equivalence, like a 2-sphere to the electromagnetic field, the magnetic flux is identified with an element in the group of integers, hence is quantized in integral multiples of some unit flux.

For the case of a (hypothetical) magnetic monopole (e.g. a magnetically charged black hole), it is the spacetime around the monopole (the complement of its worldline ℝ 0,1\mathbb{R}^{0,1} in the ambient (asymtptotically) Minkowski spacetime ℝ 3,1\mathbb{R}^{3,1}) which has the homotopy type of a 2-sphere ℝ 3,1∖ℝ 0,1≃ℝ 0,1×ℝ rad×S 2\mathbb{R}^{3,1} \setminus \mathbb{R}^{0,1} \,\simeq\, \mathbb{R}^{0,1} \times \mathbb{R}_{rad} \times S^2; this implies the Dirac charge quantization of the magnetic monopole‘s magnetic charge:

from SS21

For the case of the type II superconductor it is instead the transversal vanishing at infinity of the magnetic field (i.e. the Meissner-Ochsenfeld effect away from the vortices) which implies that the classifying map of the electromagnetic field sees not the full transversal Euclidean plane ℝ 2\mathbb{R}^2 but its one-point compactification (ℝ 2) cpt≃S 2\big( \mathbb{R}^2 \big)^{cpt} \,\simeq\, S^2, which introduces an effective 2-sphere topology onto spacetime (same as the 3-sphere in the discussion of Skyrmions and the 4-sphere in the discussion of instantons): ℝ 1,1×(ℝ 2) cpt≃ℝ 1,1×S 2\mathbb{R}^{1,1} \times \big( \mathbb{R}^2 \big)^{cpt} \,\simeq\, \mathbb{R}^{1,1} \times S^2. This implies the superconductor’s magnetic flux quantization:

from SS21

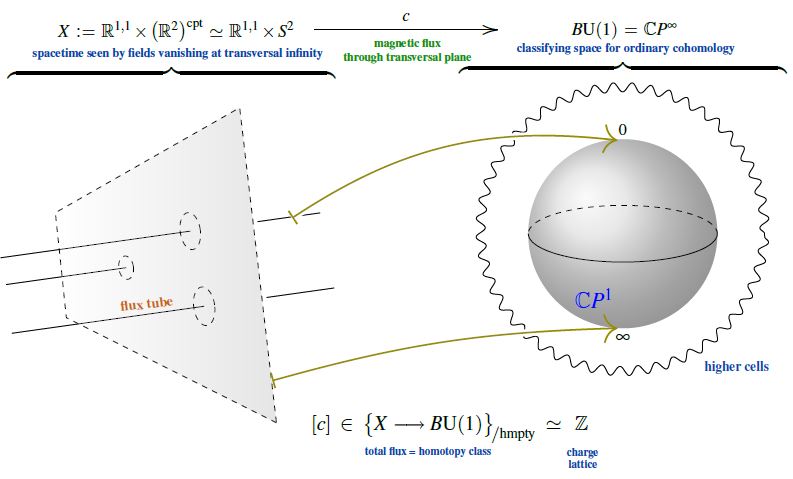
The argument that is given in most references, via consideration of the period of the vector potential on a large circle around the superconductor (e.g. Timm 20, Section 5.3), is secretly just the analysis of this picture through the clutching construction (the direct 2d analog of the discussion at SU(2)-Instantons – From the correct maths to the traditional physics story).

References

General

Comprehensive survey:

  • www.phys.nthu.edu.tw: Superconductivity, lecture slides [I:pdf, II:pdf, III:pdf, full:pdf]

Theoretical introduction and review:

See also:

Textbook account in the context of quantum materials and topological insulators:

Introducing Landau-Ginzburg models in superconductivity:

Introducing the dimer model:

  • Daniel S. Rokhsar and Steven A. Kivelson, Superconductivity and the Quantum Hard-Core Dimer Gas, Phys. Rev. Lett. 61, 2376 – Published 14 November 1988 (arXiv:10.1103/PhysRevLett.61.2376)

Argument that superconductors are actually topologically ordered phases of matter:

Vortices and flux quantization

Original articles:

Further discussion:

Lecture notes:

See also

First experimental detection of flux quantization in superconductors:

  • Bascom S. Deaver, Jr., William M. Fairbank, Experimental Evidence for Quantized Flux in Superconducting Cylinders, Phys. Rev. Lett. 7, 43 – Published 15 (1961) (doi:10.1103/PhysRevLett.7.43)

  • R. Doll, M. Näbauer, Experimental Proof of Magnetic Flux Quantization in a Superconducting Ring, Phys. Rev. Lett. 7, 51 (1961) (doi:10.1103/PhysRevLett.7.51)

More on the experimental detection magnetic flux quantization and vortices:

More theoretically flavored discussion of the flux quantization mechanism:

On the vortex flux tubes as dynamical vortex strings:

On superfluidity/superconductivity of anyons:

Superconducting qbits

On realizing qbits and quantum gates (hence quantum computation) via quantum states of magnetic flux through (Josephson junctions in) superconductors, manipulated via electromagnetic pulses:

Monograph:

  • Chen, Church, Englert, Henkel, Rohwedder, Scully, Zubairy, section 9 of: Quantum Computing Devices Principles, Designs, and Analysis, Routledge (2007) [ISBN:9780367390372]

Fine detail of the pulse control:

  • M. Werninghaus, D. J. Egger, F. Roy, S. Machnes, F. K. Wilhelm, S. Filipp: Leakage reduction in fast superconducting qubit gates via optimal control, npj Quantum Information 7 14 (2021) [[doi:10.1038/s41534-020-00346-2]]

  • M. Carroll, S. Rosenblatt, P. Jurcevic, I. Lauer & A. Kandala. Dynamics of superconducting qubit relaxation times, npj Quantum Information 8 132 (2022) [[doi:10.1038/s41534-022-00643-y]]

  • Elisha Siddiqui Matekole, Yao-Lung L. Fang, Meifeng Lin, Methods and Results for Quantum Optimal Pulse Control on Superconducting Qubit Systems, 2022 IEEE International Parallel and Distributed Processing Symposium Workshops (2022) [[arXiv:2202.03260, doi:10.1109/IPDPSW55747.2022.00102]]

Corrections due to quasiparticle-excitations:

Anyons in topological superconductors

On anyon-excitations in topological superconductors.

via Majorana zero modes:

Original proposal:

  • Nicholas Read, Dmitry Green, Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries, and the fractional quantum Hall effect, Phys. Rev. B61:10267, 2000 (arXiv:cond-mat/9906453)

Review:

  • Sankar Das Sarma, Michael Freedman, Chetan Nayak, Majorana Zero Modes and Topological Quantum Computation, npj Quantum Information 1, 15001 (2015) (nature:npjqi20151)

  • Nur R. Ayukaryana, Mohammad H. Fauzi, Eddwi H. Hasdeo, The quest and hope of Majorana zero modes in topological superconductor for fault-tolerant quantum computing: an introductory overview (arXiv:2009.07764)

  • Yusuke Masaki, Takeshi Mizushima, Muneto Nitta, Non-Abelian Anyons and Non-Abelian Vortices in Topological Superconductors &lbrack;arXiv:2301.11614&rbrack;

Further developments:

via Majorana zero modes restricted to edges of topological insulators:

  • Biao Lian, Xiao-Qi Sun, Abolhassan Vaezi, Xiao-Liang Qi, and Shou-Cheng Zhang, Topological quantum computation based on chiral Majorana fermions, PNAS October 23, 2018 115 (43) 10938-10942; first published October 8, 2018 (doi:10.1073/pnas.1810003115)

See also:

  • Yusuke Masaki, Takeshi Mizushima, Muneto Nitta, Non-Abelian Anyons and Non-Abelian Vortices in Topological Superconductors [[arXiv:2301.11614]]

Discussion via AdS/CFT

Discussion of superconductivity via AdS/CFT in condensed matter physics:

High T cT_c-superconductivity

Via topological phases of matter:

  • M. C. Diamantini, C. A. Trugenberger, V. M. Vinokur, Topological Nature of High Temperature Superconductivity (arXiv:2009.01763)

Last revised on May 31, 2024 at 13:39:07. See the history of this page for a list of all contributions to it.

EditDiscussPrevious revisionChanges from previous revisionHistory (37 revisions) Cite Print Source