nLab vortex string

Idea

By a vortex string one typically means a string-shaped soliton threading through a vortex-solution in a 4-dimensional gauge theory.

The original example are the magnetic flux tubes through the Abrikosov vortices seen in type II superconductors at critical values of the magnetic field. The idea to think of these as string-like dynamical objects in themselves, much as in string theory, is due to Nielsen-Olesen 73, hence one also speaks of Nielsen-Oleson vortices or Nielsen-Olesen strings.

More generally, such string-shaped vortices are considered in Yang-Mills theories with non-abelian gauge group (see e.g. Tong 09).

Details

Magnetic flux quantization in type II superconductors

Due to the Meissner-Ochsenfeld effect, a superconductor placed in a sufficiently small external magnetic field $H_{ext} \lt H_{c_1}$ (aligned along some axis) “expels” that field , making the total magnetic field in the bulk of the superconductor vanish. However, as the ambient magnetic field exceeds a critical value $H_{c_1}$, this behaviour changes:

• for type I superconductors, the superconducting state simply breaks down as $H_{ext} \gt H_{c_1}$ and the ambient magnetic field fully penetrates the material as for any normal conductor;

• for type II superconductors the superconducting state eventually also breaks down as $H_{ext} \gt H_{c_2} \gt H_{c_1}$, but there is an intermediate parameter region $H_{c_1} \lt H_{ext} \lt H_{c_2}$ where both regimes mix:

From Chapman 09

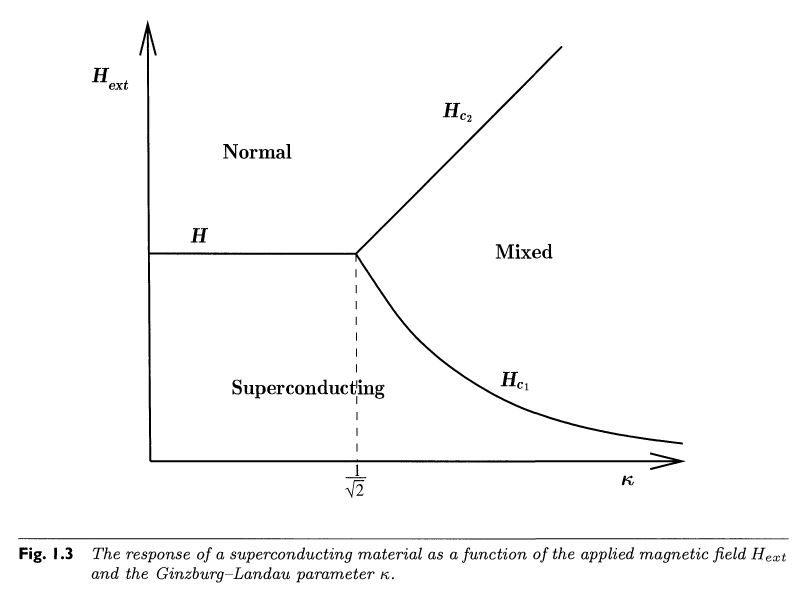
In this mixed regime, a finite number of elementary units of magnetic flux enter the superconductor, carried by little flux tubes inside vortices of electric currents: vortex strings (about a micron in diameter, e.g. Chapman 00, p. 559). Each vortex core carries one unit of magnetic flux – also called a fluxon – while at some small finite distance away from all vortices, the bulk magnetic flux in the superconductor still vanishes (mathematically: it vanishes at infinity, cf. eg. Chapman 2009 (2.31), Timm 2020 (6.101)) :

(1)

adapted from Loudon and Midgley 2009

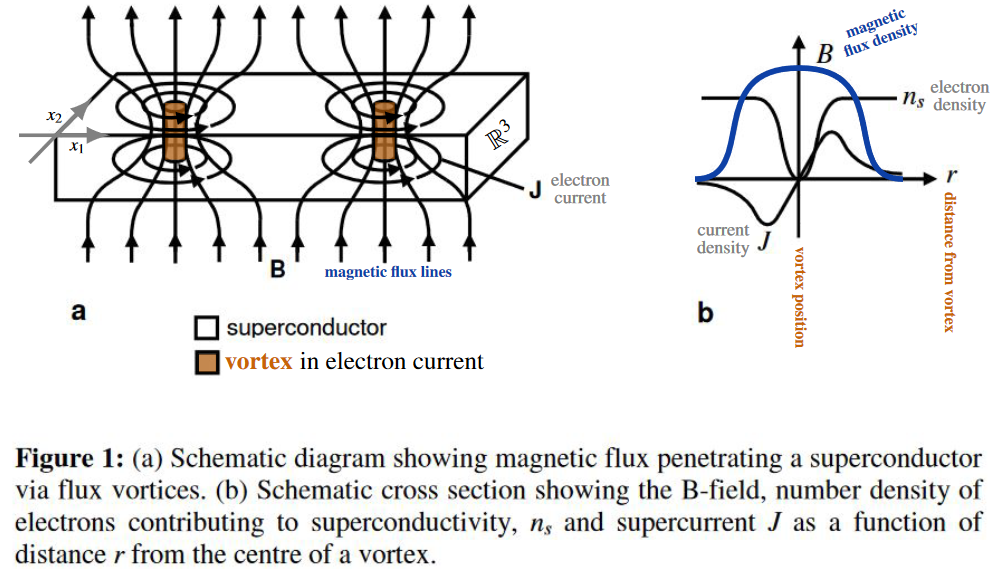
At sufficiently large density these vortices arrange into hexagonal patterns, first described by Abrikosov 57, whence also known as Abrikosov vortices.

(2)

from Yu 2012

This flux quantization in type II superconductors is traditionally explained via the effective field theory provided by the Landau-Ginzburg model; the derivation may be found reviewed in Chapman 00 (Section 2, culminating in (2.33)).

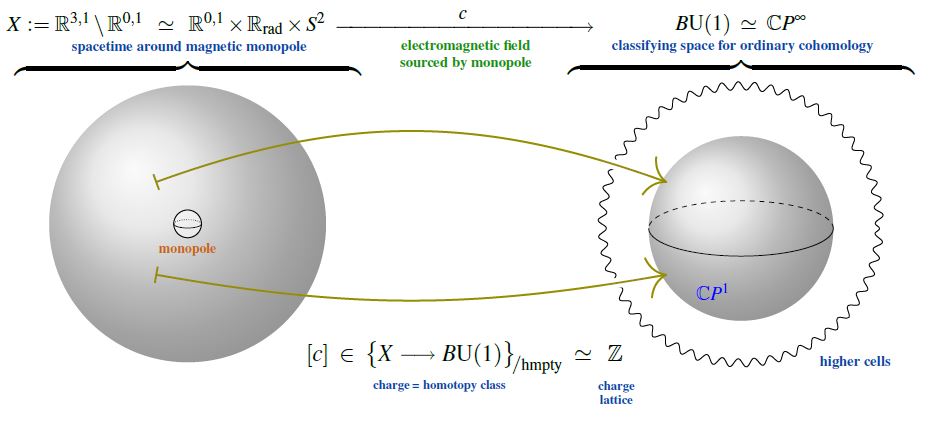
But, as indicated a little more explicitly in Alvarez-Gaumé 98 (Section IV.B, culminating below IV.11), the flux quantization as such is mathematically a direct consequence of the global topological nature of the electromagnetic field, the argument being the direct 2-dimensional analog of the quantization of instantons in QCD in 4d (see also at SU(2)-Instantons – From the correct maths to the traditional physics story) and in fact is but a slight variation of the argument for Dirac charge quantization of magnetic monopoles:

Namely, the electromagnetic field is a connection on a circle bundle, and hence the cohomology classifying space for the topological class of the electromagnetic field is the classifying space $B \mathrm{U}(1)$ of the circle group, which, being an Eilenberg-MacLane space $K(\mathbb{Z},2)$, has second homotopy group the integers:

$$\pi_2(B \mathrm{U}(1)) \;\simeq\; \big\{ S^2 \to B \mathrm{U}(1)\big\}_{\big/hmpty} \;\simeq\; \mathbb{Z} \,.$$

This implies that on every spacetime which looks, up to homotopy equivalence, like a 2-sphere to the electromagnetic field, the magnetic flux is identified with an element in the group of integers, hence is quantized in integral multiples of some unit flux.

For the case of a (hypothetical) magnetic monopole (e.g. a magnetically charged black hole), it is the spacetime around the monopole (the complement of its worldline $\mathbb{R}^{0,1}$ in the ambient (asymtptotically) Minkowski spacetime $\mathbb{R}^{3,1}$) which has the homotopy type of a 2-sphere $\mathbb{R}^{3,1} \setminus \mathbb{R}^{0,1} \,\simeq\, \mathbb{R}^{0,1} \times \mathbb{R}_{rad} \times S^2$; this implies the Dirac charge quantization of the magnetic monopole‘s magnetic charge:

from SS21

For the case of the type II superconductor it is instead the transversal vanishing at infinity of the magnetic field (i.e. the Meissner-Ochsenfeld effect away from the vortices) which implies that the classifying map of the electromagnetic field sees not the full transversal Euclidean plane $\mathbb{R}^2$ but its one-point compactification $\big( \mathbb{R}^2 \big)^{cpt} \,\simeq\, S^2$, which introduces an effective 2-sphere topology onto spacetime (same as the 3-sphere in the discussion of Skyrmions and the 4-sphere in the discussion of instantons): $\mathbb{R}^{1,1} \times \big( \mathbb{R}^2 \big)^{cpt} \,\simeq\, \mathbb{R}^{1,1} \times S^2$. This implies the superconductor’s magnetic flux quantization:

from SS21

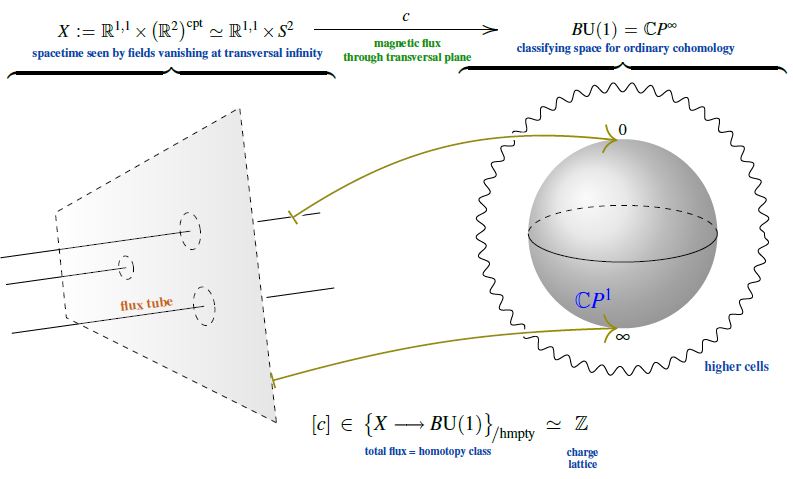
The argument that is given in most references, via consideration of the period of the vector potential on a large circle around the superconductor (e.g. Timm 20, Section 5.3), is secretly just the analysis of this picture through the clutching construction (the direct 2d analog of the discussion at SU(2)-Instantons – From the correct maths to the traditional physics story).

Related cocepts

• Abrikosov vortex

• cosmic string

• defect brane

References

In electromagnetism

Vortex strings were originally considered in the abelian gauge theory of electromagnetism as Abrikosov vortices in type II superconductors.

• Alexei Abrikosov, On the Magnetic properties of superconductors of the second group, Sov. Phys. JETP 5 (1957) 1174-1182, Zh. Eksp. Teor. Fiz. 32 (1957) 1442-1452 (spire:9138)

The idea that these vortex flux tube could be thought of as dynamical strings much as in string theory is due to:

• Holger Bech Nielsen, Poul Olesen, Vortex-line models for dual strings, Nuclear Physics B Volume 61, 24 September 1973, Pages 45-61 (doi:10.1016/0550-3213(73)90350-7)

See also

• Wikipedia, Nielsen-Olesen vortex

In Yang-Mills theory

A more general picture of vortex strings in Yang-Mills theory with nonabelian gauge group (in fact in D=4 N=2 super Yang-Mills theory):

• Amihay Hanany, David Tong, Vortices, Instantons and Branes, JHEP 0307 (2003) 037 (arXiv:hep-th/0306150)

• Amihay Hanany, David Tong, Vortex Strings and Four-Dimensional Gauge Dynamics, JHEP 0404 (2004) 066 (arXiv:hep-th/0403158)

reviewed in:

• David Tong, Quantum Vortex Strings: A Review, Annals Phys. 324:30-52, 2009 (arXiv:0809.5060)

• David Tong, Vortices, Strings, and Vortex Strings (pdf)

As probe D1-branes of D1-D5 brane bound states in a context of AdS-QCD duality:

• Joseph Polchinski, Matthew Strassler, p. 34 of: The String Dual of a Confining Four-Dimensional Gauge Theory (arXiv:hep-th/0003136)

• Roberto Auzzi, S. Prem Kumar, Section 5.2 in: Non-Abelian k-Vortex Dynamics in $\mathcal{N} = 1^\ast$ theory and its Gravity Dual, JHEP 0812:077, 2008 (arXiv:0810.3201)

On vortex strings in $\mathcal{N}=2$ super QCD identified as superstrings in type II string theory compactified on a conifold:

• Mikhail Shifman, A. Yung, Supersymmetric Solitons and How They Help Us Understand Non-Abelian Gauge Theories, Rev. Mod. Phys. 79 1139 (2007) [doi:10.1103/RevModPhys.79.1139, arXiv:hep-th/0703267

• Mikhail Shifman, A. Yung, Supersymmetric Solitons, Cambridge University Press (2009) [doi:10.1017/CBO9780511575693]

• Mikhail Shifman, A. Yung, Critical String from Non-Abelian Vortex in Four Dimensions,

  Physics Letters B 750 (2015) 416-419 [arXiv:1502.00683, doi:10.1016/j.physletb.2015.09.045 ]

• P. Koroteev, Mikhail Shifman, A. Yung, Studying Critical String Emerging from Non-Abelian Vortex in Four Dimensions, Phys.Lett. B 759 (2016) 154-158 [arXiv:1605.01472, doi:10.1016/j.physletb.2016.05.075 ]