nLab piecewise flat spacetime
Context
Riemannian geometry
Gravity
Formalism
Definition
Spacetime configurations
Properties
Spacetimes
| black hole spacetimes | vanishing angular momentum | positive angular momentum |
|---|---|---|
| vanishing charge | Schwarzschild spacetime | Kerr spacetime |
| positive charge | Reissner-Nordstrom spacetime | Kerr-Newman spacetime |
Quantum theory
Contents
Idea
If one allows pseudo-Riemannian manifolds with conical singularities then it makes sense to ask for spacetimes which are flat (isometric to pieces of Minkowski spacetime) away from strata of positive codimension, with all curvature concentrated in conical singularities on these lower-dimensional strata.
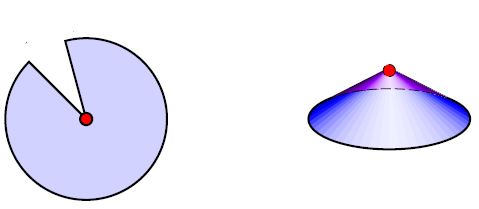
Such piecewise flat spacetimes have been considered as discretized models for smooth (non-singular and non-piecewise flat) spacetimes useful for computation (see Williams & Tuckey 1992): A combinatorial functional on piecewise flat spacetimes, depending on the edge lengths of a metric simplicial complex, was introduced by Regge 1961 (see also Barrett 1987) with the idea that in an appropriate limit it approaches the Einstein-Hilbert action functional on non-singular spacetimes. This has become famous as Regge calculus. That this limit indeed works out has been proven (only) in Cheeger, Mueller &Schrader 1984, see Cheeger 2016 for review.
A variant of this perspective, but with the conical singularities constrained to be timelike as expected for “physical” singularities, has been initiated in ‘t Hooft 2008 and worked out in some detail by van de Meent 2011.
In both cases a more speculative motivation for considering piecewise flat spacetimes is the hope that it might help with defining quantum gravity, non-perturbatively (Regge & Williams 2000). A direct attempt to define and compute a path integral quantization over piecewise flat spacetimes is known as “causal dynamical triangulation” (see Ambjorn, Jurkiewicz &Loll 20000).
Piecewise flat spacetimes appear naturally in 3-dimensional gravity, which provides much of the inspiration and motivation of various approaches.
But piecewise flat spacetimes also appear naturally as the “far-horizon geometry” (“small -limit”, see there) of BPS black brane spacetimes in supergravity theories, where considerations such as discussed at M-theory on G₂-manifolds suggest that the conical singularities have to be taken seriously as part of the physical model. These cone brane-singularities are necessarily time-like, as in ‘t Hooft 2008, van de Meent 2011, but in contrast to the assumption in general Regge calculus and generally of higher (co)dimension.
References
Regge calculus
-
Tullio Regge, General relativity without coordinates, Nuovo Cim (1961) 19: 558 (doi:10.1007/BF02733251)
-
Charles Misner, Kip Thorne, John Wheeler, §42 in: Gravitation, W. H. Freeman (1973) [inspire:95654]
-
Jeff Cheeger, Werner Müller, Robert Schrader, On the curvature of piecewise flat spaces, Comm. Math. Phys. Volume 92, Number 3 (1984), 405-454 (euclid:1103940867)
-
John Barrett, The geometry of classical Regge calculus, Classical and Quantum Gravity, Volume 4, Number 6, 1987 (doi:10.1088/0264-9381/4/6/015/meta)
-
R. M. Williams, P. A. Tuckey, Regge calculus: a brief review and bibliography, Classical and Quantum Gravity, Volume 9, Number 5, 1992 (web)
-
Tullio Regge, Ruth M. Williams, Discrete structures in gravity, J. Math. Phys.41:3964-3984, 2000 (arXiv:gr-qc/0012035)
-
Jeff Cheeger, Curvature of piecewise flat spaces, talk at Courant institute 2016 (pdf, pdf)
-
Aleksandar Miković, Piecewise Flat Metrics and Quantum Gravity (arXiv:2001.11439)
-
Aleksandar Miković: Finiteness of piecewise flat quantum gravity with matter [arXiv:2412.17465]
See also
- Wikipedia, Regge calculus
Application to FRW models of cosmology:
- Ren Tsuda, Takanori Fujiwara, Oscillating 4-Polytopal Universe in Regge Calculus (arXiv:2011.04120)
‘t Hooft-van de Meent
-
Gerard 't Hooft, A locally finite model for gravity, Found. Phys. 38:733-757, 2008 (arXiv:0804.0328)
-
Maarten van de Meent: Piecewise Flat Gravitational Waves, Class. Quant. Grav.28:075005, 2011 (arXiv:1012.1991)
-
Maarten van de Meent, Exact Piecewise Flat Gravitational Waves, Class. Quantum Grav. 28 (2011) 245006 (arXiv:1106.5380)
-
Maarten van de Meent, Piecewise Flat Gravity in 3+1 dimensions (arXiv:1111.6468)
Causal Dynamical Triangulation
On the idea of numerical path integrals over causally triangulated spacetimes as an approach to quantum gravity:
-
Jan Ambjørn, Renate Loll: Non-perturbative Lorentzian Quantum Gravity, Causality and Topology Change, Nucl. Phys. B 536 (1998) 407-434 [arXiv:hep-th/9805108, doi:10.1016/S0550-3213(98)00692-0]
-
Jan Ambjørn, J. Jurkiewicz, Renate Loll: Dynamically Triangulating Lorentzian Quantum Gravity_, Nucl. Phys. B 610 (2001) 347-382 [arXiv:hep-th/0105267, doi:10.1016/S0550-3213(01)00297-8]
-
Jan Ambjørn, J. Jurkiewicz, Renate Loll: A non-perturbative Lorentzian path integral for gravity&, Phys. Rev. Lett. 85 (2000) 924-927 [arXiv:hep-th/0002050, doi:10.1103/PhysRevLett.85.924]
Review:
-
Jan Ambjørn, J. Jurkiewicz, Renate Loll: Causal Dynamical Triangulations and the Quest for Quantum Gravity, in: Foundations of Space and Time, Cambridge University Press (2012) [arXiv:1004.0352, doi:10.1017/CBO9780511920998.013]
-
Renate Loll: Quantum Gravity from Causal Dynamical Triangulations: A Review, Class. Quantum Grav. 37 013002 [arXiv:1905.08669, doi:10.1088/1361-6382/ab57c7 ]
-
Jan Ambjørn, Lattice Quantum Gravity: EDT and CDT, in Handbook of Quantum Gravity, Springer (2023) [arXiv:2209.06555]
-
Dario Benedetti, Landau Theory of Causal Dynamical Triangulations, in: Handbook of Quantum Gravity, Springer (2023) [arXiv:2212.11043]
-
Jan Ambjørn, Renate Loll: Causal Dynamical Triangulations: Gateway to Nonperturbative Quantum Gravity, in Encyclopedia of Mathematical Physics 2nd ed, Elsevier (2024) [arXiv:2401.09399]
-
Jan Ambjørn: Causal Dynamical Triangulation, Scholarpedia (2024) [webpage]
-
Renate Loll: Nonperturbative quantum gravity unlocked through computation, in: Quantum Gravity and Computation, Routledge (2025) [arXiv:2501.17972]
See also:
- Wikipedia: Causal Dynamical Triangulation
Possible relation to dark energy:
-
Mingwei Dai, Walter Freeman, Jack Laiho, Marc Schiffer, Judah Unmuth-Yockey: Dynamical Dark Energy from Lattice Quantum Gravity [arXiv:2408.08963]
-
Axel Maas, Simon Plätzer, Felix Pressler: Hints for a Geon from Causal Dynamic Triangulations [arXiv:2504.11047]
Last revised on June 13, 2025 at 07:24:24. See the history of this page for a list of all contributions to it.