nLab large 1/N limit

Idea

In the context of the 't Hooft double line construction and the AdS/CFT correspondence with $N_c \in \mathbb{N}$ colors, the small $N$ region or large $1/N_c$ limit is the situation away from the large N limit. In this large $1/N_c$ limit perturbative string theory-corrections (for small 't Hooft coupling $\lambda = g_{YM}^2 N_c$) and/or M-theory-corrections (for small $N_c$) to the supergravity-approximation of the AdS/CFT correspondence are relevant.

In application to phenomenology, the small $N_c$ region (and hence M-theory) is what is ultimately relevant for the AdS/QCD correspondence, given that quantum chromodynamics has a small number $N_c^{QCD} = 3$ of quark colors:

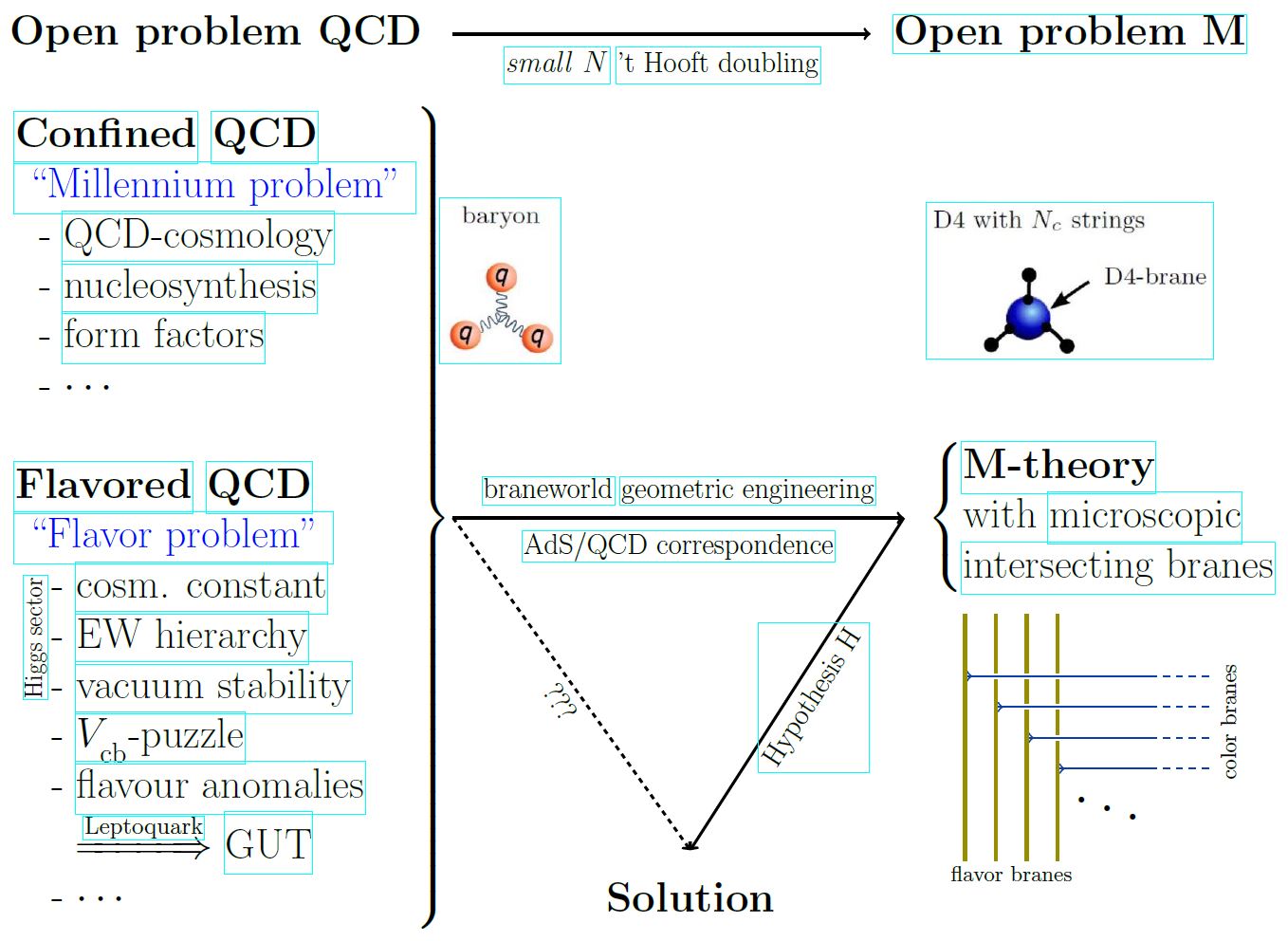
References

General

On the general relevance of M-theory at small $N_c$ in gauge/gravity duality:

• Leonard Susskind, Another Conjecture about M(atrix) Theory (arXiv:hep-th/9704080)

  (in the context of the BFSS matrix model)

• Nissan Itzhaki, Juan Maldacena, Jacob Sonnenschein, Shimon Yankielowicz, Supergravity and The Large $N$ Limit of Theories With Sixteen Supercharges, Phys. Rev. D 58, 046004 (1998) (arXiv:hep-th/9802042)

  (phase diagrams in $N_c$ and 't Hooft coupling for various Dp-brane species)

On the logical equivalence between the four-colour theorem and a statement about transition from the small N limit to the large N limit for Lie algebra weight systems on Jacobi diagrams via the 't Hooft double line construction:

• Dror Bar-Natan, Lie Algebras and the Four Color Theorem, Combinatorica 17-1(1997) 43–52 (arXiv:q-alg/9606016, doi:10.1007/BF01196130)

In AdS/CFT

General

• B. Basso, Cusp anomalous dimension in planar maximally supersymmetric Yang-Mills theory (spire:858223)

  “The result $[$(29)$]$ coincides exactly with the recent two-loop stringy correction computed in Alday-Maldacena 07, providing a striking confirmation of the AdS/CFT correspondence.”

• David Jorrin, Nicolas Kovensky, Martin Schvellinger, Towards $1/N$ corrections to deep inelastic scattering from the gauge/gravity duality, JHEP 04 (2016) 113 (arXiv:1601.01627)

Discussion of small N corrections via a lattice QFT-Ansatz on the AdS side of AdS2/CFT1:

• Richard C. Brower, Cameron V. Cogburn, A. Liam Fitzpatrick, Dean Howarth, Chung-I Tan, Lattice Setup for Quantum Field Theory in $AdS_2$ (arXiv:1912.07606)

Via conformal bootstrap

Using the conformal bootstrap for CFTs at small N to deduce M-theory-properties on the dual side:

• Nathan B. Agmon, Shai Chester, Silviu S. Pufu, Solving M-theory with the Conformal Bootstrap, JHEP 06 (2018) 159 (arXiv:1711.07343)

• Shai Chester, Bootstrapping M-theory, 2018 (pdf)

Specifically for the D=6 N=(2,0) SCFT on the M5-brane via AdS7/CFT6:

• Shai Chester, Eric Perlmutter, M-Theory Reconstruction from $(2,0)$ CFT and the Chiral Algebra Conjecture, J. High Energ. Phys. (2018) 2018: 116 (arXiv:1805.00892)

• Luis Alday, Shai Chester, Himanshu Raj, 6d $(2,0)$ and M-theory at 1-loop (arXiv:2005.07175)

Specifically for the D=3 SCFT (BLG-model, ABJM model) on the M2-brane via AdS4/CFT3

• Nathan B. Agmon, Shai Chester, Silviu S. Pufu, The M-theory Archipelago (arXiv:1907.13222)

Specifically in AdS5/CFT4 via D3-brane contributions:

• Yosuke Imamura, Finite-$N$ superconformal index via the AdS/CFT correspondence (arXiv:2108.12090)

In AdS/QCD

Discussion of small N corrections specifically in holographic QCD:

• B. Basso, Cusp anomalous dimension in planar maximally supersymmetric Yang-Mills theory, Continuous Advances in QCD 2008, pp. 317-328 (2008) (spire:858223, doi:10.1142/9789812838667_0027)

  “The result $[$(29)$]$ coincides exactly with the recent two-loop stringy correction computed in Alday-Maldacena 07, providing a striking confirmation of the AdS/CFT correspondence.”

• H. Dorn, H.-J. Otto, On Wilson loops and $Q\bar Q$-potentials from the AdS/CFT relation at $T\geq 0$, In: A. Ceresole, C. Kounnas , Dieter Lüst, Stefan Theisen (eds.) Quantum Aspects of Gauge Theories, Supersymmetry and Unification Lecture Notes in Physics, vol 525. Springer 2007 (arXiv:hep-th/9812109, doi:10.1007/BFb0104268)

• Masayasu Harada, Shinya Matsuzaki, and Koichi Yamawaki, Implications of holographic QCD in chiral perturbation theory with hidden local symmetry, Phys. Rev. D 74, 076004 (2006) (doi:10.1103/PhysRevD.74.076004)

  (with an eye towards hidden local symmetry in chiral perturbation theory)

• Csaba Csaki, Matthew Reece, John Terning, The AdS/QCD Correspondence: Still Undelivered, JHEP 0905:067, 2009 (arXiv:0811.3001)

• Salvatore Baldino, Stefano Bolognesi, Sven Bjarke Gudnason, Deniz Koksal, A Solitonic Approach to Holographic Nuclear Physics, Phys. Rev. D 96, 034008 (2017) (arXiv:1703.08695)

• Edward Witten, Some Milestones in the Study of Confinement, talk at Prospects in Theoretical Physics 2023 – Understanding Confinement, IAS (2023) [web, YT]

  26:26: “by now it’s clear [Lucini & Teper 2001] that lattice gauge theory, at least for the glueball sector, has made it clear that the $1/N$-expansion is a good approximation to the real world, especially if you include a leading correction to the large $N$ limit. Now unfortunately this is best established in the glueball sector, which is not very accessible experimentally.”

  28:56: “but the $1/N$ expansion doesn’t explain everything. In fact, it’s not hard to find phenomena in meson physics where the $1/N$-expansion does not work well.”

  36:15: “I suspect the $1/N$-expansion works reasonably well for many aspects of baryons. However, as for mesons, it is easy to point to things that won’t work well for baryons. In particular, among other things, I don’t think the $1/N$ expansion will be successful for nuclei as opposed to individual nucleons.”

  37:12: “I don’ t think the phenomenological models used by nuclear physicists would have any success at of if the large N limit was a good description of nuclei.”

In 2d QCD

On 1/N corrections in 2d QCD:

• Itzhak Bars, QCD and Strings in 2D (arXiv:hep-th/9312018)