nLab Spin(7) manifold
Context
Riemannian geometry
Contents
Idea
An 8-manifold of special holonomy Spin(7).
Equivalently: an 8-manifold equipped with a globalization of the Cayley 4-form.
Properties
As part of the Berger classification
classification of special holonomy manifolds by Berger's theorem:
As -Riemannian manifolds
(Leung 02)
As exceptional geometry
Spin(8)-subgroups and reductions to exceptional geometry
see also: coset space structure on n-spheres
Relation to tangentially twisted Cohomotopy
On a spin-manifold of dimension 8 a choice of topological Spin(7)-structure is equivalently a choice of cocycle in J-twisted Cohomotopy cohomology theory. This follows (FSS 19, 3.4) from
-
the standard coset space-structures on the 7-sphere (see here)
-
the fact that coset spaces are the homotopy fibers of the maps of the corresponding classifying spaces (see here)
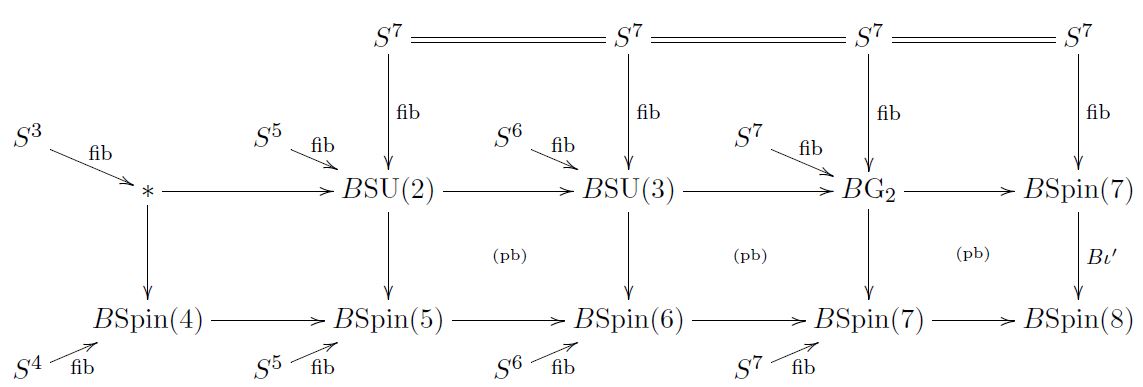
Characteristic classes
Proposition
Let be a closed smooth manifold of dimension 8 with Spin structure. If the frame bundle moreover admits G-structure for
then the Euler class , the second Pontryagin class and the cup product-square of the first Pontryagin class (the combination proportional to the I8-term) of the frame bundle/tangent bundle are related by
Remark
The same conclusion (1) also holds for Spin(5).Spin(3)-structure, see there.
See also at C-field tadpole cancellation.
Related concepts
References
General
The concept goes back to:
- E. Bonan, (1966), Sur les variétés riemanniennes à groupe d’holonomie G2 ou Spin(7), C. R. Acad. Sci. Paris 262: 127–129.
Characterization in terms of the Euler 8-class and the I8-invariant polynomial of the tangent bundle:
- H. Blaine Lawson, Marie-Louise Michelsohn, Thm. 10.7 in: Spin geometry, Princeton University Press (1989) [ISBN 9780691085425]
Construction of compact Spin(7)-manifolds:
-
Christine Taylor, Compact Manifolds with Holonomy Spin(7) (1996) (pdf)
-
Dominic Joyce, A new construction of compact 8-manifolds with holonomy , J. Differential Geom. Volume 53, Number 1 (1999), 89-130 (euclid:jdg/1214425448)
-
Dominic Joyce, Compact Manifolds with Special Holonomy, Oxford Mathematical Monographs, Oxford University Press (2000) (ISBN:9780198506010)
In terms of G-structure:
- Robert Bryant, Metrics with Exceptional Holonomy, Annals of Mathematics Second Series, Vol. 126, No. 3 (Nov., 1987), pp. 525-576 (jstor:1971360)
and motivated from special supersymmetry (such as in M-theory on Spin(7)-manifolds):
-
Chris Isham, Christopher Pope, Nowhere Vanishing Spinors and Topological Obstructions to the Equivalence of the NSR and GS Superstrings, Class. Quant. Grav. 5 (1988) 257 (spire:251240, doi:10.1088/0264-9381/5/2/006)
-
Chris Isham, Christopher Pope, Nicholas Warner, Nowhere-vanishing spinors and triality rotations in 8-manifolds, Classical and Quantum Gravity, Volume 5, Number 10, 1988 (cds:185144, doi:10.1088/0264-9381/5/10/009)
(focus on Spin(7)-structure)
- Ya. V. Bazaikin, On the new examples of complete noncompact Spin(7)-holonomy metrics, Sib Math J 48, 8–25 (2007) (doi:10.1007/s11202-007-0003-7)
Relation to Higgs bundles
Relating M-theory on Spin(7)-manifolds with F-theory on Spin(7)-manifolds via Higgs bundles:
- Mirjam Cvetic, Jonathan Heckman, Thomas B. Rochais, Ethan Torres, Gianluca Zoccarato, Geometric Unification of Higgs Bundle Vacua (arXiv:2003.13682)
Last revised on April 28, 2024 at 13:52:18. See the history of this page for a list of all contributions to it.