nLab de Sitter spacetime

Definition

Full de Sitter spacetime is the Lorentzian manifold which is the coset space of Lorentz groups

$$dS^d \simeq O(d,1)/O(d-1,1)$$

This models a cosmology FRW model for positive cosmological constant/dark energy.

Similarly anti de Sitter spacetime is

$$adS^d \simeq O(d-1,2)/O(d-1,1)$$

(e.g. Blau §39.1)

This admits different spatial slicings of relevance:

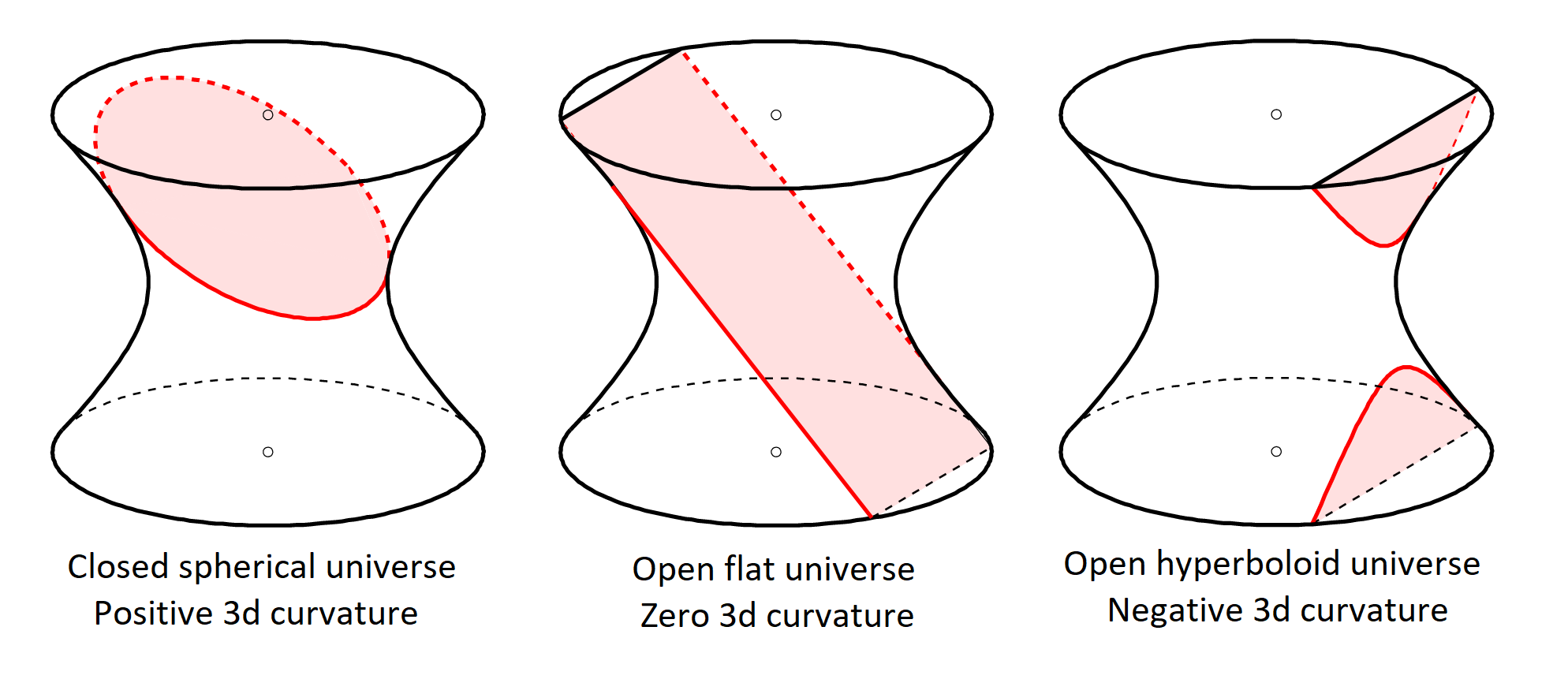
graphics grabbed from this Physics.SE comment

Related concepts

geometric context	gauge group	stabilizer subgroup	local model space	local geometry	global geometry	differential cohomology	first order formulation of gravity
differential geometry	Lie group/algebraic group $G$	subgroup (monomorphism) $H \hookrightarrow G$	quotient (“coset space”) $G/H$	Klein geometry	Cartan geometry	Cartan connection
examples	Euclidean group $Iso(d)$	rotation group $O(d)$	Cartesian space $\mathbb{R}^d$	Euclidean geometry	Riemannian geometry	affine connection	Euclidean gravity
	Poincaré group $Iso(d-1,1)$	Lorentz group $O(d-1,1)$	Minkowski spacetime $\mathbb{R}^{d-1,1}$	Lorentzian geometry	pseudo-Riemannian geometry	spin connection	Einstein gravity
	anti de Sitter group $O(d-1,2)$	$O(d-1,1)$	anti de Sitter spacetime $AdS^d$				AdS gravity
	de Sitter group $O(d,1)$	$O(d-1,1)$	de Sitter spacetime $dS^d$				deSitter gravity
	linear algebraic group	parabolic subgroup/Borel subgroup	flag variety	parabolic geometry
	conformal group $O(d,t+1)$	conformal parabolic subgroup	Möbius space $S^{d,t}$		conformal geometry	conformal connection	conformal gravity
supergeometry	super Lie group $G$	subgroup (monomorphism) $H \hookrightarrow G$	quotient (“coset space”) $G/H$	super Klein geometry	super Cartan geometry	Cartan superconnection
examples	super Poincaré group	spin group	super Minkowski spacetime $\mathbb{R}^{d-1,1\vert N}$	Lorentzian supergeometry	supergeometry	superconnection	supergravity
	super anti de Sitter group		super anti de Sitter spacetime
higher differential geometry	smooth 2-group $G$	2-monomorphism $H \to G$	homotopy quotient $G//H$	Klein 2-geometry	Cartan 2-geometry
	cohesive ∞-group	∞-monomorphism (i.e. any homomorphism) $H \to G$	homotopy quotient $G//H$ of ∞-action	higher Klein geometry	higher Cartan geometry	higher Cartan connection
examples			extended super Minkowski spacetime		extended supergeometry		higher supergravity: type II, heterotic, 11d

References

In classical gravity

• Leonardo Castellani, Riccardo D'Auria, Pietro Fré, volume 1, chapter I.3.8 of Supergravity and Superstrings - A Geometric Perspective, World Scientific (1991) [doi:10.1142/0224, ch I.3: pdf, ch I.4: pdf]

• Matthias Blau, §39 of: Lecture notes on general relativity (web)

• Thomas Hartman, Lecture Notes on Classical de Sitter Space (pdf, pdf)

• Marcus Spradlin, Andrew Strominger, Anastasia Volovich, Les Houches Lectures on De Sitter Space (arXiv:hep-th/0110007)

See also:

• Wikipedia, de Sitter space

With focus on methods of conformal geometry:

• Juan A. Valiente Kroon, chapter 15 of: Conformal Methods in General Relativity, Cambridge University Press (2017, 2022) [doi:10.1017/9781009291309, oapen:20.500.12657/59217, pdf]

Further discussion of the de Sitter group and its representation theory:

• Vladimir Schaub, A Walk Through $Spin(1,d+1)$ [arXiv:2405.01659]

In perturbative quantum gravity

Discussion of de Sitter spacetime in perturbative quantum gravity and its infrared instability, includes the following:

• Emil Mottola, Particle creation in de Sitter space, Phys. Rev. D 31, 754 – Published 15 February 1985 (doi:10.1103/PhysRevD.31.754)

• Edward Witten, Quantum Gravity In De Sitter Space, talk at Strings 2001, (arXiv:hep-th/0106109)

• Dietmar Klemm, Luciano Vanzo, Aspects of Quantum Gravity in de Sitter Spaces, Journal of Cosmology and Astroparticle Physics, Volume 2004, November 2004 (arXiv:hep-th/0407255)

• Richard Woodard, De Sitter Breaking in Field Theory (arXiv:gr-qc/0408002)

• Alexander Polyakov, De Sitter Space and Eternity, Nucl.Phys.B797:199-217, 2008 (arXiv:0709.2899)

• Alexander Polyakov, Decay of Vacuum Energy, Nucl.Phys.B834:316-329, 2010 (arXiv:0912.5503)

• Dmitry Krotov, Alexander Polyakov, Infrared Sensitivity of Unstable Vacua, Nucl.Phys.B 849 (2011) 410-432 (arXiv:1012.2107)

• Alexander Polyakov, Infrared instability of the de Sitter space (arXiv:1209.4135)

• Paul R. Anderson, Emil Mottola, On the Instability of Global de Sitter Space to Particle Creation, Phys. Rev. D 89, 104038 (2014) (arXiv:1310.0030)

• Paul Anderson, Emil Mottola, Quantum Vacuum Instability of ‘Eternal’ de Sitter Space, Phys. Rev. D 89, 104039 (2014) (arXiv:1310.1963)

• Arvind Rajaraman, de Sitter Space is Unstable in Quantum Gravity, Phys. Rev. D 94, 125025 (2016) (arXiv:1608.07237)

• Paul Anderson, Emil Mottola, Dillon H. Sanders, Decay of the de Sitter Vacuum, Phys. Rev. D 97, 065016 (2018) (arXiv:1712.04522)

In string/M-theory

A no-go theorem for KK-compactifications of supergravity down to de Sitter spacetime is claimed in

• Juan Maldacena, Carlos Nunez, Supergravity description of field theories on curved manifolds and a no go theorem, Int.J.Mod.Phys. A16 (2001) 822-855 (arXiv:hep-th/0007018)

Discussion of de Sitter perturbative string theory vacua and their role in the landscape of string theory vacua or else in the swampland:

• David Kutasov, Travis Maxfield, Ilarion Melnikov, Savdeep Sethi, Constraining de Sitter Space in String Theory, Phys. Rev. Lett. 115, 071305 (2015) (arXiv:1504.00056)

• Jakob Moritz, Ander Retolaza, Alexander Westphal, Towards de Sitter from 10D, Phys. Rev. D 97, 046010 (2018) (arXiv:1707.08678)

• Savdeep Sethi, Supersymmetry Breaking by Fluxes (arXiv:1709.03554)

  re-amplified in:

  Savdeep Sethi, Hope or No Hope for a String Landscape?, talk at StringPheno2019 (pdf pdf)

• Ulf Danielsson, Thomas Van Riet, What if string theory has no de Sitter vacua?, International Journal of Modern Physics D, Vol. 27, No. 12, 1830007 (2018) (arXiv:1804.01120, doi:10.1142/S0218271818300070)

  (problems with KKLT 03)

• Thomas Van Riet, Is dS space in the Swampland, talk at StringPheno18 (pdf slides)

• Thomas Van Riet, Status of KKLT, talk at Simons summer workshop 2018 (recording)

• Ulf Danielsson, The quantum swampland (arXiv:1809.04512)

  (argues that the issue with stringy de Sitter moduli stabilization raised in Sethi 17 is related to the de Sitter instability seen in QFT, according to the references above)

• Georges Obied, Hirosi Ooguri, Lev Spodyneiko, Cumrun Vafa, De Sitter Space and the Swampland (arXiv:1806.08362)

• Jakob Moritz, Ander Retolaza, Alexander Westphal, On uplifts by warped anti-D3-branes (arXiv:1809.06618)

• Iosif Bena, Emilian Dudas, Mariana Graña, Severin Lüst, Uplifting Runaways (arXiv:1809.06861)

• Clay Cordova, G. Bruno De Luca, Alessandro Tomasiello, Classical de Sitter Solutions of Ten-Dimensional Supergravity (arXiv:1812.04147)

• Michael Dine, Jamie A.P. Law-Smith, Shijun Sun, Duncan Wood, Yan Yu, Obstacles to Constructing de Sitter Space in String Theory (arXiv:2008.12399)

In view of alpha' higher curvature corrections:

• Ivano Basile, Alessia Platania, String Tension between de Sitter vacua and Curvature Corrections (arXiv:2103.06276)

  “We show that the resulting higher-derivative $\alpha'$-corrections forbid the existence of de Sitter vacua, at least in regimes where string-loop corrections can be neglected.”

• Liam McAllister, Jakob Moritz, Richard Nally, Andreas Schachner, Candidate de Sitter Vacua [arXiv:2406.13751]

  “Finding vacua that demonstrably survive subleading corrections, and in which the quantization conditions are completely understood, is an important open problem for which this work has prepared the foundations.”

On de Sitter spacetime cosmology realized in brane world models in ambient $\sim$AdS-bulk spacetime:

• Souvik Banerjee, Ulf Danielsson, Giuseppe Dibitetto, Suvendu Giri, Marjorie Schillo, Emergent de Sitter cosmology from decaying AdS (arXiv:1807.01570)

• Souvik Banerjee, Ulf Danielsson, Giuseppe Dibitetto, Suvendu Giri, Marjorie Schillo, de Sitter Cosmology on an expanding bubble (arXiv:1907.04268)

Discussion in the context of M-theory on G2-manifolds:

• Beatriz de Carlos, Andre Lukas, Stephen Morris, Non-perturbative vacua for M-theory on G2 manifolds, JHEP 0412:018, 2004 (arxiv:hep-th/0409255)

  which concludes that with taking non-perturbative effects from membrane instantons into account one gets 4d vacua with vanishing and negative cosmological constant (Minkowski spacetime and anti-de Sitter spacetime) but not with positive cosmological constant (de Sitter spacetime). They close by speculating that M5-brane instantons might yield de Sitter spacetime.

• Johan Blåbäck, Ulf Danielsson, Giuseppe Dibitetto, Suvendu Giri, Constructing stable de Sitter in M-theory from higher curvature corrections (arXiv:1902.04053)

  which suggests that including higher curvature corrections makes it work

• Iosif Bena, Alex Buchel, Severin Lüst, Throat destabilization (for profit and for fun) (arxiv:1910.08094)

For analogous discussion of embedding of the ekpyrotic cosmology-scenario into string theory/type IIA supergravity:

• Kunihito Uzawa, No-Go theorems for ekpyrosis from ten-dimensional supergravity, J. High Energ. Phys. (2018) 2018: 41 (arXiv:1803.11084, doi:10.1007/JHEP06(2018)041)

  reviewed in:

  Kunihito Uzawa, Ekpyrotic scenario in string theory (pdf)

Discussion of asymptotic de Sitter spacetimes from time-dependent KK-compactification of type II supergravity:

• Paul Marconnet, Dimitrios Tsimpis, Universal accelerating cosmologies from 10d supergravity, J. High Energ. Phys. 2023 33 (2023) [arXiv:2210.10813, doi:10.1007/JHEP01(2023)033]

reviewed in:

• Dimitrios Tsimpis, Universal accelerating cosmologies from 10d supergravity, talk at M-Theory and Mathematics 2023, NYU Abu Dhabi (Jan 2023) [slides:pdf, video:video: YT, web]

and further discussed in:

• David Andriot, Dimitrios Tsimpis, Timm Wrase, Accelerated expansion of an open universe, and string theory realizations [arXiv:2309.03938]