nLab immersion of smooth manifolds
Context
Étale morphisms
Differential geometry
synthetic differential geometry
Introductions
from point-set topology to differentiable manifolds
geometry of physics: coordinate systems, smooth spaces, manifolds, smooth homotopy types, supergeometry
Differentials
Tangency
The magic algebraic facts
Theorems
Axiomatics
Models
differential equations, variational calculus
Chern-Weil theory, ∞-Chern-Weil theory
Cartan geometry (super, higher)
Contents
Definition
Let be a differentiable function between smooth manifolds (or just differentiable manifolds) of finite dimension.
We denote by , the tangent bundles and by the fiber product of differentiable functions into . In particular, is the pullback bundle of along to a real vector bundle over .
Definition
The differentiable function is called an immersion precisely if the canonical map
is a monomorphism.
This map is the one induced from the universal property of the pullback by the commuting diagram
given by the differential of going between the tangent bundles.
Equivalently this means the following:
Definition
The function is an immersion precisely if for every point the differential
between the tangent space of at and the tangent space of at is an injection.
Definition
(embedding of smooth manifolds)
An immersion whose underlying continuous function is an embedding of topological spaces is called an an embedding of smooth manifolds.
Example
(immersions that are not embeddings)
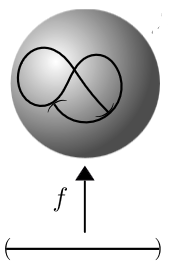
Consider an immersion of an open interval into the Euclidean plane (or the 2-sphere) as shown on the right. This is not an embedding of smooth manifolds: around the points where the image crosses itself, the function is not even injective, but even at the points where it just touches itself, the pre-images under of open subsets of do not exhaust the open subsets of , hence do not yield the subspace topology.
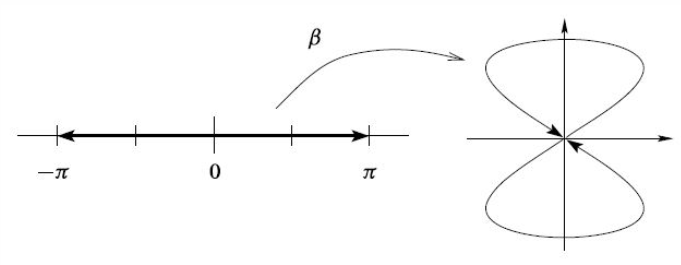
Concretely, consider the function sin sin. While this is an immersion and injective, it fails to be an embedding due to the points at “touching” the point at .
figure from Lee (2012, Fig. 4.3)
Properties
Relation to embeddings
Immersion are precisely the “local embeddings”:
Proposition
A smooth map of smooth manifolds is an immersion precisely if for every point there is an open neighbourhood such that is an embedding of smooth manifolds.
Since moreover the embeddings of smooth manifolds admit local slice charts (see there) so do immersions.
In the generality of supermanifolds this is Varadarajan 2004, Thm. 4.4.3.
Relation to formal immersions
The related concept of formal immersion of smooth manifolds, defined as an injective bundle morphism between tangent bundles, is in some ways easier to study, in the sense that the collection of all such formal immersions, , is simpler to analyze. Then under some conditions on and (see there), it is the case that the map is a weak homotopy equivalence. This is a case of the h-principle.
Characterization in differential cohesion
A smooth function between smooth manifolds is canonically regarded as a morphism in the cohesive (∞,1)-topos SynthDiff∞Grpd. With respect to the canonical infinitesimal neighbourhood inclusion Smooth∞Grpd SynthDiff∞Grpd there is a notion of formally unramified morphism in .
is an immersion precisely if it is formally unramified with respect to this infinitesimal cohesion.
See the discussion at SynthDiff∞Grpd for details.
Variants
The algebraic geometry analogue of a submersion is a smooth morphism.
The analogue between arbitrary topological spaces (not manifolds) is simply an open map. There is also topological submersion, of which there are two versions.
Related concepts
References
-
William M. Boothby, Def. III 4.3 in: An introduction to differentiable manifolds and Riemannian geometry, Academic Press (1975, 1986), Elsevier (2002) [ISBN:9780121160517, pdf]
-
John Lee, Chapter 4 of: Introduction to Smooth Manifolds, Springer (2012) [doi:10.1007/978-1-4419-9982-5, book webpage, pdf]
Discussion in the generality of supermanifolds:
- Veeravalli Varadarajan, pp. 148 in: Supersymmetry for mathematicians: An introduction, Courant Lecture Notes in Mathematics 11, American Mathematical Society (2004) [doi:10.1090/cln/011]
Last revised on May 18, 2024 at 14:28:13. See the history of this page for a list of all contributions to it.