nLab vortex

Idea

A kind of soliton.

From Thuneberg

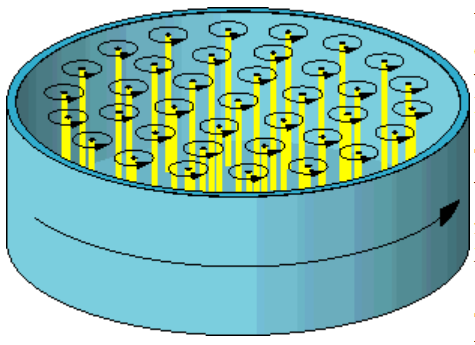
Examples

Magnetic flux quantization in type II superconductors

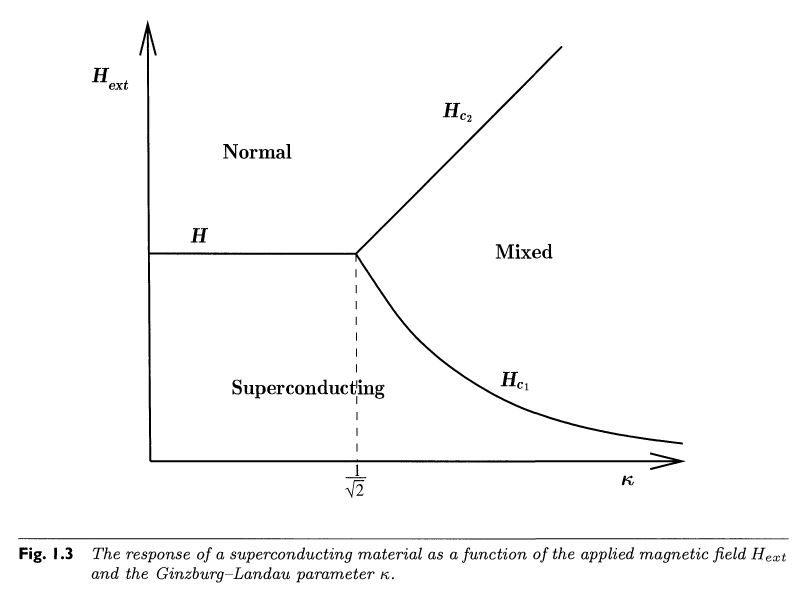
Due to the Meissner-Ochsenfeld effect, a superconductor placed in a sufficiently small external magnetic field $H_{ext} \lt H_{c_1}$ (aligned along some axis) “expels” that field , making the total magnetic field in the bulk of the superconductor vanish. However, as the ambient magnetic field exceeds a critical value $H_{c_1}$, this behaviour changes:

• for type I superconductors, the superconducting state simply breaks down as $H_{ext} \gt H_{c_1}$ and the ambient magnetic field fully penetrates the material as for any normal conductor;

• for type II superconductors the superconducting state eventually also breaks down as $H_{ext} \gt H_{c_2} \gt H_{c_1}$, but there is an intermediate parameter region $H_{c_1} \lt H_{ext} \lt H_{c_2}$ where both regimes mix:

From Chapman 09

In this mixed regime, a finite number of elementary units of magnetic flux enter the superconductor, carried by little flux tubes inside vortices of electric currents: vortex strings (about a micron in diameter, e.g. Chapman 00, p. 559). Each vortex core carries one unit of magnetic flux – also called a fluxon – while at some small finite distance away from all vortices, the bulk magnetic flux in the superconductor still vanishes (mathematically: it vanishes at infinity, cf. eg. Chapman 2009 (2.31), Timm 2020 (6.101)) :

(1)

adapted from Loudon and Midgley 2009

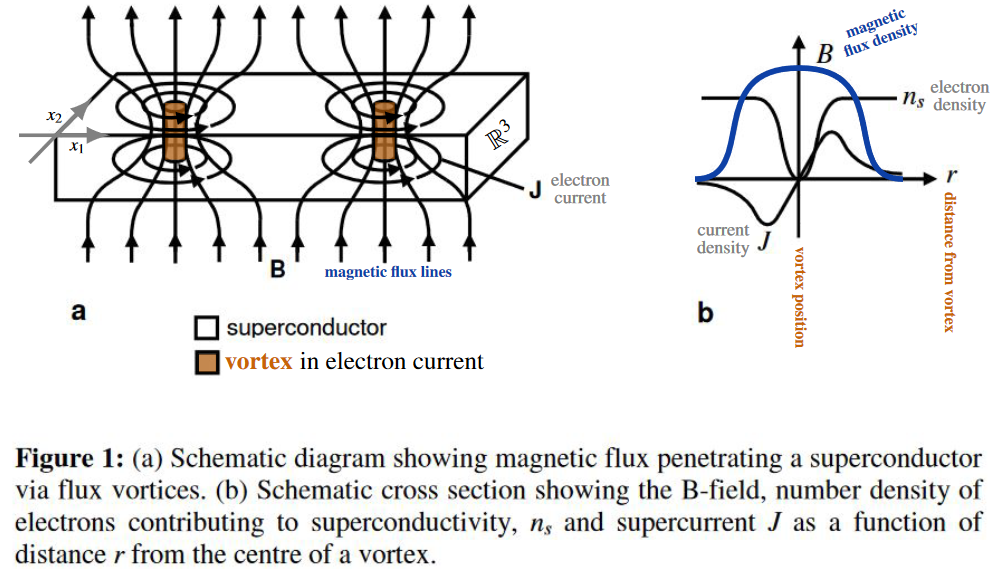
At sufficiently large density these vortices arrange into hexagonal patterns, first described by Abrikosov 57, whence also known as Abrikosov vortices.

(2)

from Yu 2012

This flux quantization in type II superconductors is traditionally explained via the effective field theory provided by the Landau-Ginzburg model; the derivation may be found reviewed in Chapman 00 (Section 2, culminating in (2.33)).

But, as indicated a little more explicitly in Alvarez-Gaumé 98 (Section IV.B, culminating below IV.11), the flux quantization as such is mathematically a direct consequence of the global topological nature of the electromagnetic field, the argument being the direct 2-dimensional analog of the quantization of instantons in QCD in 4d (see also at SU(2)-Instantons – From the correct maths to the traditional physics story) and in fact is but a slight variation of the argument for Dirac charge quantization of magnetic monopoles:

Namely, the electromagnetic field is a connection on a circle bundle, and hence the cohomology classifying space for the topological class of the electromagnetic field is the classifying space $B \mathrm{U}(1)$ of the circle group, which, being an Eilenberg-MacLane space $K(\mathbb{Z},2)$, has second homotopy group the integers:

$$\pi_2(B \mathrm{U}(1)) \;\simeq\; \big\{ S^2 \to B \mathrm{U}(1)\big\}_{\big/hmpty} \;\simeq\; \mathbb{Z} \,.$$

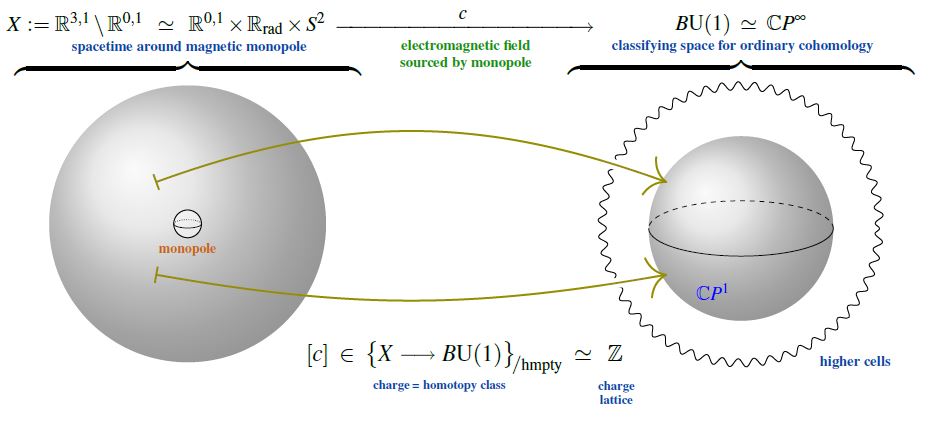
This implies that on every spacetime which looks, up to homotopy equivalence, like a 2-sphere to the electromagnetic field, the magnetic flux is identified with an element in the group of integers, hence is quantized in integral multiples of some unit flux.

For the case of a (hypothetical) magnetic monopole (e.g. a magnetically charged black hole), it is the spacetime around the monopole (the complement of its worldline $\mathbb{R}^{0,1}$ in the ambient (asymtptotically) Minkowski spacetime $\mathbb{R}^{3,1}$) which has the homotopy type of a 2-sphere $\mathbb{R}^{3,1} \setminus \mathbb{R}^{0,1} \,\simeq\, \mathbb{R}^{0,1} \times \mathbb{R}_{rad} \times S^2$; this implies the Dirac charge quantization of the magnetic monopole‘s magnetic charge:

from SS21

For the case of the type II superconductor it is instead the transversal vanishing at infinity of the magnetic field (i.e. the Meissner-Ochsenfeld effect away from the vortices) which implies that the classifying map of the electromagnetic field sees not the full transversal Euclidean plane $\mathbb{R}^2$ but its one-point compactification $\big( \mathbb{R}^2 \big)^{cpt} \,\simeq\, S^2$, which introduces an effective 2-sphere topology onto spacetime (same as the 3-sphere in the discussion of Skyrmions and the 4-sphere in the discussion of instantons): $\mathbb{R}^{1,1} \times \big( \mathbb{R}^2 \big)^{cpt} \,\simeq\, \mathbb{R}^{1,1} \times S^2$. This implies the superconductor’s magnetic flux quantization:

from SS21

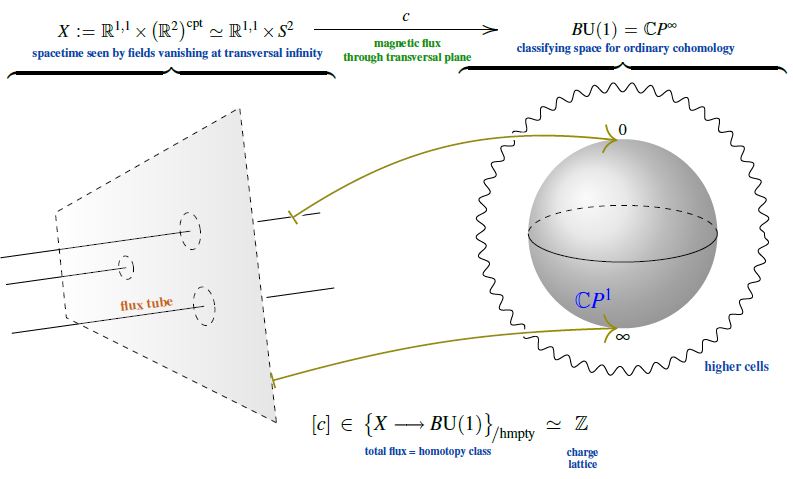
The argument that is given in most references, via consideration of the period of the vector potential on a large circle around the superconductor (e.g. Timm 20, Section 5.3), is secretly just the analysis of this picture through the clutching construction (the direct 2d analog of the discussion at SU(2)-Instantons – From the correct maths to the traditional physics story).

Vortex anyons

See Votex anyons at braid group statistics.

Related concepts

• instanton

• monopole

• vortex string

• Skyrmion

• domain wall

• cosmic string

References

General

A historical abandoned but influential speculation on vortex strings:

• Lord Kelvin, On Vortex Atoms

Reviews and surveys:

• David Tong, TASI Lectures on Solitons (web), part 3: Vortices (pdf)

• Roberto Percacci, section 2.6 in: Non-Perturbative Quantum Field Theory – An Introduction to Topological and Semiclassical Methods, SISSA & ICTP (2024) [doi:10.22323/9788898587056, pdf]

On water vortices forming knots:

• Dustin Kleckner and William T. M. Irvine, Creation and dynamics of knotted vortices, Nature Physics 9 (2013) 253–258 [doi:10.1038/nphys2560]

On quantum vortices as in superconductors or Bose-Einstein condensates/superfluids:

• Rufus Phillips, Quantum Vortices.

• Erkki Thuneberg, Superfluidity and Quantized Vortices

• K. R. Sreenivasan, Vortices, particles and superfluidity (pdf, pdf)

Discussion via AdS/CMT:

• Markus A. G. Amano, Minoru Eto, Holographic Global Vortices with Novel Boundary Conditions [arXiv:2404.03212]

On stable vortex knots in Bose-Einstein condensates:

• Yuta Nozaki, Yuya Koda, Muneto Nitta: Quantum Knots that Never Come Untied Michikazu Kobayashi [arXiv:2410.07470]

Defect anyons

Often the concept of anyons is introduced as if a generalization of perturbative quanta like fundamental bosons and fermions. But many (concepts of) types of anyons are really solitonic$\;$defects such as vortices.

The general concept of braiding of defects in solid state physics:

• N. David Mermin, The topological theory of defects in ordered media, Rev. Mod. Phys. 51 (1979) 591 $[$doi:10.1103/RevModPhys.51.591$]$

  (including a review of basic homotopy theory)

and more specifically for vortices:

• Hoi-Kwong Lo, John Preskill, Non-Abelian vortices and non-Abelian statistics, Phys. Rev. D 48 (1993) 4821 $[$doi:10.1103/PhysRevD.48.4821$]$

Explicit discussion in terms of anyons:

• Alexei Kitaev, Anyons in an exactly solved model and beyond, Annals of Physics 321 1 (2006) 2-111 $[$doi:10.1016/j.aop.2005.10.005$]$

  Anyonic particles are best viewed as a kind of topological defects that reveal nontrivial properties of the ground state. $[$p. 4$]$

Concrete vortex$\;$anyons in Bose-Einstein condensates:

• B. Paredes, P. Fedichev, J. Ignacio Cirac, Peter Zoller: 1/2-Anyons in small atomic Bose-Einstein condensates, Phys. Rev. Lett. 87 (2001) 010402 [doi:10.1103/PhysRevLett.87.010402, arXiv:cond-mat/0103251]

• Julien Garaud, Jin Dai, Antti J. Niemi, Vortex precession and exchange in a Bose-Einstein condensate, J. High Energ. Phys. 2021 157 (2021) $[$arXiv:2010.04549$]$

• Thomas Mawson, Timothy Petersen, Joost Slingerland, Tapio Simula, Braiding and fusion of non-Abelian vortex anyons, Phys. Rev. Lett. 123 (2019) 140404 $[$doi:10.1103/PhysRevLett.123.140404$]$

and in (other) superfluids:

• Yusuke Masaki, Takeshi Mizushima, Muneto Nitta, Non-Abelian Half-Quantum Vortices in 3P2 Topological Superfluids $[$arXiv:2107.02448$]$

and in condensates of non-defect anyons:

• Michele Correggi, Romain Duboscq, Douglas Lundholm, Nicolas Rougerie, Vortex patterns in the almost-bosonic anyon gas, Europhys. Lett. 126 (2019), 20005 $[$arXiv:1901.10739, doi:10.1209/0295-5075/126/20005$]$

See also Ahn, Park & Yang 19 who refer to the band nodes in the Brillouin torus of a semi-metal as “vortices in momentum space”.

And see at defect brane.