Schreiber Anyonic defect branes in TED K-theory
An article that we have written:
-
Hisham Sati and Urs Schreiber:
Anyonic Defect Branes and Conformal Blocks in
Twisted Equivariant Differential (TED) K-Theory
Reviews in Mathematical Physics
35 06 (2023) 2350009
download:
-
pdf (more references added on as codim=2 defects; some typose fixed)
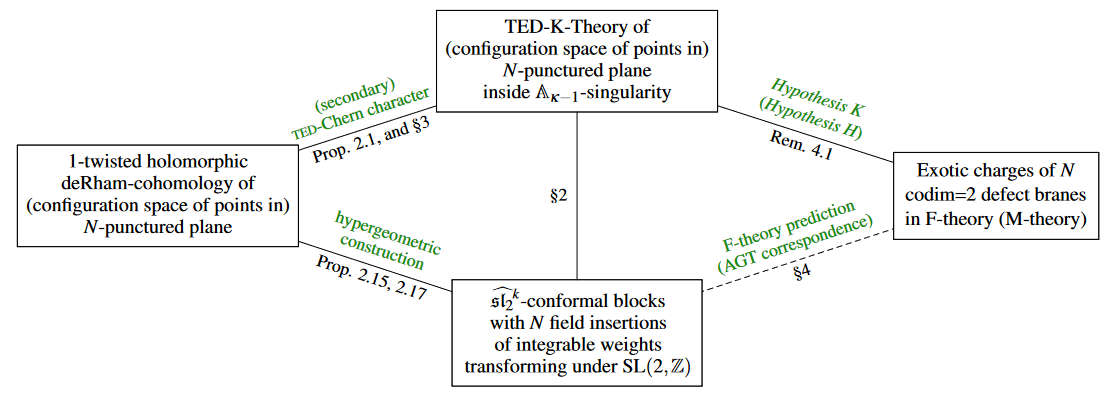
Abstract: We demonstrate that twisted equivariant differential K-theory of transverse complex curves accommodates exotic charges of the form expected of codimension=2 defect branes, such as of D7-branes in IIB/F-theory on -type orbifold singularities, but also of their dual 3-brane defects of class-S theories on M5-branes. These branes have been argued, within F-theory and the AGT correspondence, to carry special -monodromy charges not seen for other branes, at least partially reflected in conformal blocks of the -WZW model over their transverse punctured complex curve. Indeed, it has been argued that all "exotic" branes of string theory are defect branes carrying such U-duality monodromy charges – but none of these had previously been identified in the expected brane charge quantization law given by K-theory.
Here we observe that it is the subtle (and previously somewhat neglected) twisting of equivariant K-theory by flat complex line bundles appearing inside orbi-singularities (“inner local systems”) that makes the secondary Chern character on a punctured plane inside an -type singularity evaluate to the twisted holomorphic de Rham cohomology which Feigin, Schechtman and Varchenko showed realizes -conformal blocks, here in degree 1 – in fact it gives the direct sum of these over all admissible fractional levels . The remaining higher-degree -conformal blocks appear similarly if we assume our previously discussed “Hypothesis H” about brane charge quantization in M-theory. Since conformal blocks – and hence these twisted equivariant secondary Chern characters – solve the Knizhnik-Zamolodchikov equation and thus constitute representations of the braid group of motions of defect branes inside their transverse space, this provides a concrete first-principles realization of anyon statistics of – and hence of topological quantum computation on – defect branes in string/M-theory.
Related articles:
-
Hisham Sati and Urs Schreiber:
-
Hisham Sati and Urs Schreiber:
-
Hisham Sati and Urs Schreiber:
Differential Cohomotopy implies intersecting brane observables
-
David Corfield, Hisham Sati and Urs Schreiber:
-
Hisham Sati and Urs Schreiber:
-
Hisham Sati and Urs Schreiber:
For more see at Hypothesis H.
Expository talk:
-
via Seminario de Categorías UNAM, 13 April 2022
-
download:
talk slides pdf

Related talks:
Last revised on August 20, 2024 at 18:30:33. See the history of this page for a list of all contributions to it.