nLab 3-brane in 6d
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
Idea
There is supposed to be a -brane in 6-dimensional super-spacetime given by the Green-Schwarz action functional induced by the exceptional super Lie algebra -cocycle on (Hughes-Liu-Polchinski 86).
This is thought to be the intersection locus of two M5-branes (Papadopoulos & Townsend 1996, Tseytlin 1996, Howe, Lambert & West 1998, p. 2, Kachru, Oz & Yin 1998), hence the M-theory lift of D4/NS5-brane intersection.
Since this brane has codimension 2, it is a defect brane.
Related concepts
The brane scan.
The Green-Schwarz type super -brane sigma-models (see at table of branes for further links and see at The brane bouquet for the full classification):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 11 | M2 | M5 | ||||||||
| 10 | D0 | F1, D1 | D2 | D3 | D4 | NS5, D5 | D6 | D7 | D8 | D9 |
| 9 | * | |||||||||
| 8 | * | |||||||||
| 7 | M2 | |||||||||
| 6 | F1, S1 | S3 | ||||||||
| 5 | * | |||||||||
| 4 | * | * | ||||||||
| 3 | * |
(The first columns follow the exceptional spinors table.)
The corresponding exceptional super L-∞ algebra cocycles (schematically, without prefactors):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 11 | on sIso(10,1) | on m2brane | ||||||||
| 10 | on sIso(9,1) | on StringIIA | on StringIIB | on StringIIA | on sIso(9,1) | on StringIIA | on StringIIB | in StringIIA | on StringIIB | |
| 9 | on sIso(8,1) | |||||||||
| 8 | on sIso(7,1) | |||||||||
| 7 | on sIso(6,1) | |||||||||
| 6 | on sIso(5,1) | on sIso(5,1) | ||||||||
| 5 | on sIso(4,1) | |||||||||
| 4 | on sIso(3,1) | on sIso(3,1) | ||||||||
| 3 | on sIso(2,1) |
The Brane molecule
Furthermore, there exists a more general classification of possible supermembranes in spacetime with spatial dimensions and time dimensions, appearing in (Blencowe-Duff 88). In this sense, the brane scan is but the branch of the brane molecule. The objects appearing here are expected to be related to other generalizations of string theory. See D=12 supergravity and bosonic M-theory.
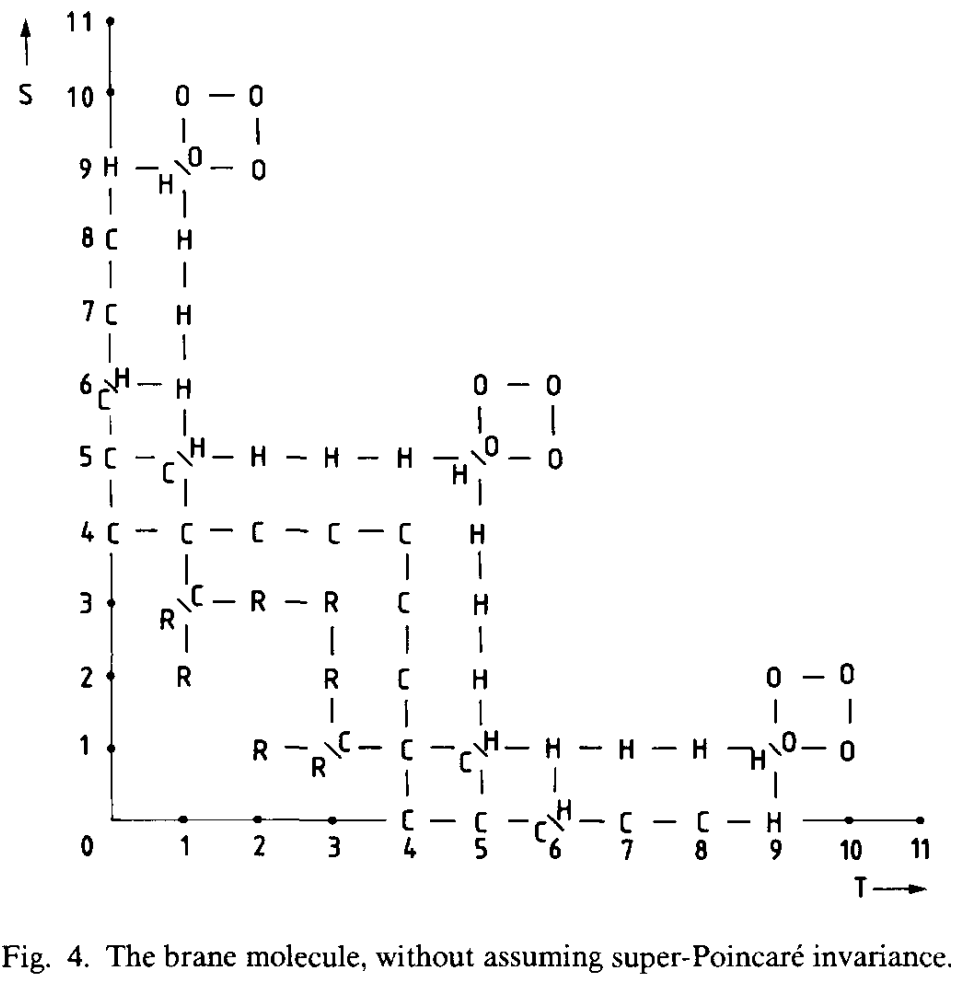
Compare:
-
Miles Blencowe, Mike Duff, Supermembranes and the Signature of Space-time, Nucl. Phys. B310 (1988) 387-404 (spire:262142, 10.1016/0550-3213(88)90155-1, pdf)
References
The original construction:
- James Hughes, Jun Liu, Joseph Polchinski, Supermembranes, Physics Letters B 180 4 (1986_ 370-374 [spire:20685]
Discussion building on that:
- Martin Rocek, Arkady Tseytlin, Partial breaking of global supersymmetry, constrained superfields, and 3-brane actions, Phys. Rev. D 59 (1999) 106001 [doi:10.1103/PhysRevD.59.106001, arXiv:hep-th/9811232]
The relevant cocycle for discussion as a Green-Schwarz sigma-model:
- Leonardo Castellani, Riccardo D'Auria, Pietro Fré, (III.7.18) of Supergravity and Superstrings - A Geometric Perspective, World Scientific, 1991
Discussion of the 3-brane in 6d explicitly as a black brane in an M5-brane/NS5-brane worldvolume:
- Paul Howe, Neil Lambert, Peter West, The Threebrane Soliton of the M-Fivebrane, Phys. Lett. B 419 (1998) 79-83 [doi:10.1016/S0370-2693(97)01433-0, arXiv:hep-th/9710033]
and the understanding of this configuration as the locus of intersecting M5-branes:
-
George Papadopoulos, Paul Townsend, Intersecting M-branes, Phys. Lett. B 380 (1996) 273 [doi:10.1016/0370-2693(96)00506-0, arXiv:hep-th/9603087]
-
Arkady Tseytlin, Harmonic superpositions of M-branes, Nucl. Phys. B 475 (1996) 149 [doi:10.1016/0550-3213(96)00328-8, arXiv:hep-th/9604035]
-
Hironori Mori: M-theory Perspectives on Codimension-2 Defects, Osaka (2016) [inspire:1519095]
-
Hironori Mori, Yuji Sugimoto: Surface Operators from M-strings, Phys. Rev. D 95 026001 (2017) [arXiv:1608.02849, doi:10.1103/PhysRevD.95.026001]
with a matrix model-description in:
- Shamit Kachru, Yaron Oz, Zheng Yin, Matrix Description of Intersecting M5 Branes JHEP 9811:004, (1998) (arXiv:hep-th/9803050)
See also
- Peter West, section 14.6.1 of: Introduction to Strings and Branes, Cambridge University Press (2012) [doi:10.1017/CBO9781139045926]
For more on this:
- Joaquim Gomis, David Mateos, Joan Simón, Paul Townsend, Brane-Intersection Dynamics from Branes in Brane Backgrounds, Phys. Lett. B 430 (1998) 231-236 [doi:10.1016/S0370-2693(98)00555-3, arXiv:hep-th/9803040]
See also:
- S. Bellucci, N. Kozyrev, S. Krivonos, A Sutulin: Component on-shell actions of supersymmetric 3-branes: I. 3-brane in , Class. Quantum Grav. 32 (2015) 035025 [doi:10.1088/0264-9381/32/3/035025, arXiv:1409.0641]
The relation to D=4 N=2 super Yang-Mills theory:
-
Paul Howe, Neil Lambert, Peter West, Classical M-Fivebrane Dynamics and Quantum Yang-Mills, Phys. Lett. B418 (1998) 85-90 (arXiv:hep-th/9710034)
-
Neil Lambert, Peter West, Gauge Fields and M-Fivebrane Dynamics, Nucl. Phys. B524 (1998) 141-158 (arXiv:hep-th/9712040)
-
Neil Lambert, Peter West, Superfields and the M-Fivebrane, Phys. Lett. B424 (1998) 281-287 (arXiv:hep-th/9801104)
-
Neil Lambert, Peter West, Monopole Dynamics from the M-Fivebrane, Nucl. Phys. B556 (1999) 177-196 (arXiv:hep-th/9811025)
and via F-theory in
- Robert de Mello Koch, Alastair Paulin-Campbell, Joao P. Rodrigues, Monopole Dynamics in super Yang-Mills Theory From a Threebrane Probe, Nucl. Phys. B559 (1999) 143-164 (arXiv:hep-th/9903207)
On quantum Seiberg-Witten curves in relation to class S-theories and M3-defect branes inside M5-branes:
- Jin Chen, Babak Haghighat, Hee-Cheol Kim, Marcus Sperling, Elliptic Quantum Curves of Class , J. High Energ. Phys. 2021 28 (2021) [arXiv:2008.05155, doi:10.1007/JHEP03(2021)028]
As M5-probe branes in an AdS7-CFT6 background (i.e. in the near horizon limit of black M5-branes):
-
Varun Gupta, Holographic M5 branes in , J. High Energ. Phys. 2021 32 (2021) [arXiv:2109.08551, doi:10.1007/JHEP12(2021)032]
-
Varun Gupta, More Holographic M5 branes in [arXiv:2301.02528]
Last revised on October 28, 2024 at 11:49:38. See the history of this page for a list of all contributions to it.