Schreiber Structure Theory for Higher WZW Terms

$\;\;\;\;\;\;\;\;\;\;\;$ Structure theory for higher WZW terms

$\;\;\;\;\;\;\;\;\;\;\;$ With application to the derivation of the cohomological nature of M-brane charge.

Abstract. The famous Wess-Zumino-Witten term in 2d conformal field theory turns out to be a fundamental concept in the intersection of Lie theory and differential cohomology: it is a Deligne 3-cocycle on a Lie group whose Dixmier-Douady class is a Lie group 3-cocycle with values in $U(1)$ and whose curvature is the corresponding Lie algebra 3-cocycle, regarded as a left-invariant form. I explain how this generalizes to higher group stacks, and how there is a natural construction from any $(p+2)$-cocycle on any super L-∞ algebra $\mathfrak{g}$ to a WZW-type Deligne cocycle on a higher super group stack $\tilde G$ integrating $\mathfrak{g}$. Every such higher WZW term serves as a local Lagrangian density, hence as an action functional for a $p$-brane sigma model on $\tilde G$, and I explain how the homotopy stabilizer group stacks of such higher WZW terms are the Lie integration of the Noether current algebras of these sigma-models. As an application, we consider the bouquet of iterated super $L_\infty$-extensions emanating from the superpoint, which turns out to be the “old brane scan” of string/M-theory completed by the branes “with tensor multiplet fields”, such as the D-branes and the M5-brane. I explain how applying the general theory of higher WZW terms to the $L_\infty$-extensions corresponding to the M2/M5-brane yields the “BPS charge M-theory super Lie algebra” together with a Lie integration to a super 6-group stack. From running a Serre spectral sequence we read off from this result how the naive nature of M5-brane charge as being in ordinary cohomology gets refined to twisted generalized cohomology in accordance with the conjectures stated in (Sati 10, section 6.3, Sati 13, section 2.5).

This is based on joint work with Domenico Fiorenza and Hisham Sati (notably Fiorenza-Schreiber-Stasheff 12, Fiorenza-Sati-Schreiber 13, Fiorenza-Sati-Schreiber 15). The statement about the Noether current algebras is due to (Sati-Schreiber 15, Schreiber-Khavkine).

These are lecture notes for

• a lecture series at: Roger Picken (org.), Seminário de Teoria Quântica do Campo Topológica, Lisbon, Jan-Mar 2016 (part I on 26 Jan 2016, part II on 29 Jan 2016, part III on 23 Feb 2016, part IV on 26 Feb 2016, part V on 15 Mar 2016, part VI on 18 Mar 2016))

• a lecture series Prequantum field theory and the Green-Schwarz WZW terms at: Harald Grosse, Danny Stevenson, Richard Szabo (org.), Higher Structures in String Theory and Quantum Field Theory, ESI Program, Vienna, November 30-December 4, 2015

• a minicourse at: Hisham Sati (org.) Flavors of Cohomology, Pittsburgh June 3-5, 2015

based on the more comprehensive lecture notes at

• geometry of physics

  • smooth homotopy types

  • prequantum geometry

  • supergeometry

  • WZW terms

  • BPS charges.

Full details are in (dcct), an expositional survey is at Higher Prequantum Geometry.

Related talk notes include:

• Obstruction theory for parameterized higher WZW terms;

• The M-Theory BPS charge super Lie 6-algebra;

• Equivariant cohomology of M2/M5-branes.

Motivation and Survey: 11d Supergravity with M-brane corrections

The term “M-theory” has come to refer to two related but distinct concepts. On the one hand it became the chiffre for the elusive hypothetical non-perturbative theory of which perturbative string theory is the perturbation theory, in a suitable limit. But in practice the term is used for something concrete and largely precise, that is expected to be the first-order approximation to this: classical 11-dimensional supergravity with M-brane effects included, such as BPS charges, membrane instanton contributions and gauge enhancement at ADE singularities (each of these is discussed in more detail below).

It turns out that all or most of these “M-brane effects” refer to the prequantum field theory of the Green-Schwarz sigma-models for the M2-brane and the M5-brane (which by charge duality also involve the KK-monopole and the M9-brane) on the given supergravity target spacetimes. A fairly decent mathematical understanding of this does actually exist in the literature, even if it is often not made very explicit.

Here we are concerned with making this mathematically fully explicit and precise, and refining the mathematics a bit more such as to see a bit further.

We find that most of what is known about “M-theory” in the restrictive sense above, and some things not known before, is all concisely enoced in definite globalizations of an higher WZW term denoted $\mathbf{L}_{M2/M5}$ (a variant of the Green-Schwarz action functional). In summary we discuss here the following:

1. There is a canonical cocycle $\mathbf{L}^X_{M2/M5}$ on 11-dimensional super-Minkowski spacetime with coefficients in the rational quaternionic Hopf fibration, which is naturally complexified by adding the associative 3-form $\alpha$;

2. a definite globalization $(\mathbf{L}^X_{M2/M5} + i \alpha^X)$ of the WZW term $\mathbf{L}_{M2} + i \alpha$ is equivalently

   1. an 11-dimensional super spacetime, possibly with orbifold singularities, and equipped with a field configuration of 11-dimensional supergravity that solves the Einstein equations of motion;

   2. which is equipped with the structure of a fibration with fibers G2-manifolds – the setup of M-theory on G2-manifolds;

   3. and equipped with classical anomaly-cancellation that makes the M2-brane- and the M5-brane Green-Schwarz sigma-model on this target spacetime be globally well defined (an issue that has been left completely open in previous literature).

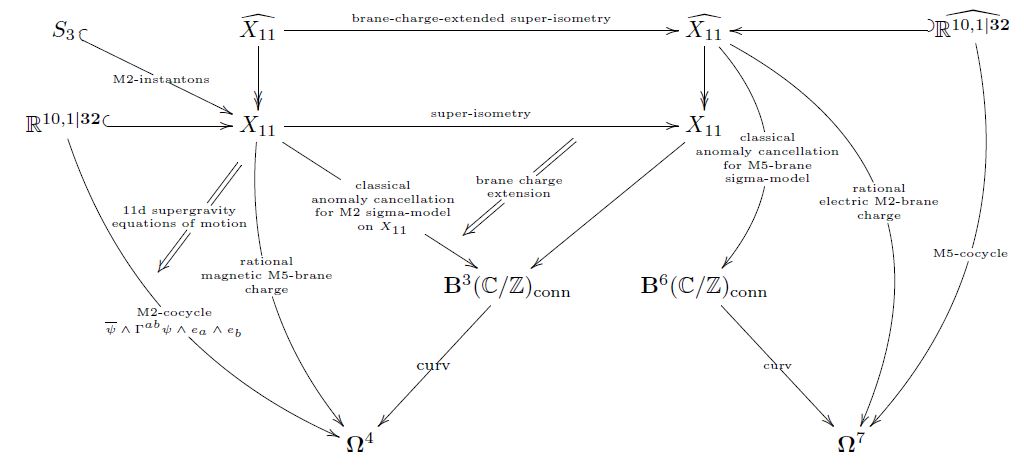
3. The higher cover of the superisometry group $Iso(X,\mathbf{L}_{M2}/M5)$ is The M-Theory BPS charge super Lie 6-algebra refinement of the M-theory super Lie algebra, whose nil-elements characterize the BPS charge of the super-spacetime.

4. The volume holonomy of $(\mathbf{L}^X_{M2} + i \alpha^X)$ over associative submanifolds are the membrane instanton contributions.

Moreover (but these two points we do not further discuss here):

• One may also see that the moduli space of local choices for $\mathbf{L}^X_{M2/M5}$, regarded as a higher prequantization of the cocycle, locally gives the fundamental representation of E7, exhibiting U-duality. But this we do not discuss here.

• The conformal field theories in the near-horizon limit of M2/M5-black brane configurations (as in AdS4/CFT3 and AdS7-CFT6) arise as the small fluctuations of the Green-Schwarz sigma-models around classical M-brane configurations embedded into the asymptotic AdS-boundary (Claus-Kallosh-Proeyen 97,Dall’Agata-Fabri-Fraser-Fré-Termonia-Trigiante 98, Claus-Kallosh-Kumar-Townsend 98, Pasti-Sorokin-Tonin 99). (This is for the abelian case of single branes, we get to the all-important nonabelian case below).

Therefore, for making progress with the open question of formulating M-theory proper, a key issue is a precise understanding of the cohomological nature of M-brane charges (Sati 10) as twisted differential cohomology along the lines above.

In these lectures here we discuss how to rigorously derive this, and a bit more, at the level of rational homotopy theory/de Rham cohomology.

Indeed, in most of the existing literature, M-brane charges are being regarded in de Rham cohomology. But it is well known (see (Distler-Freed-Moore 09) for the state of the art) that in the small coupling limit where the perturbation theory of type II string theory applies, the brane charges are not just in (twisted, self-dual) de Rham cohomology, but instead in a (twisted, self-dual) equivariant generalized cohomology theory, namely in real ($\mathbb{Z}/2$-equivariant) topological K-theory, of which de Rham cohomology is only the rational shadow under the Chern character map. This makes a crucial difference (Maldacena-Moore-Seiberg 01, Evslin-Sati 06): the differentials in the Atiyah-Hirzebruch spectral sequence for K-theory describe how de Rham cohomology classes receive corrections as they are lifted to K-theory: some charges may disappear, others may appear.

But the lift of this situation from F1/Dp-branes to M-branes had been missing. The open question is: Which equivariant generalized cohomology theory $E_G$ do M-brane charges take values in?

brane theory	generalized cohomology theory for brane charges
F1/Dp-branes in type II string theory	twisted K-theory
M2/M5 in M-theory	open

These lectures here are to prepare the ground for mathematically addressing this question. Discussion of the non-rational generalized M-brane cohomology thery itself is beyond the scope of this lecture, but see the talk Equivariant cohomology of M2/M5-branes.

Session I

We recall the definition of Deligne cohomology, of the Deligne cocycle which is the traditional WZW term and of L-∞ algebras. Then we discuss the $L_\infty$-algebra of infinitesimal symmetries of any Deligne cocycle on a manifold, called the “Poisson bracket L-∞ algebra”.

In Session II we generalize this to higher WZW terms defined on higher group stacks and and Session III we generalize to the finite symmetries of these higher WZW terms, which form themselves a higher group stack.

Deligne cohomology of manifolds

It is familiar from Dirac charge quantization and from prequantization, that when given a closed differential 2-form $\omega$, then the extra data needed in order to have a circle group-valued parallel transport along paths such that for contractible paths it equals the integral of $\omega$ over a cobounding disk, is a $U(1)$-principal connection $\nabla$ with curvature $F_\nabla = \omega$.

The concept of a cocycle in degree-$(p+2)$ Deligne cohomology is precisely the generalization of this situation as $\omega$ is generalized to a closed $(p+2)$-form, for any $p \in \mathbb{N}$ and parallel transport is generalized to higher parallel transport over $(p+1)$-dimensional “worldvolumes”. Generally one may think of such a cocycle as representing a circle (p+1)-bundle with connection. For $p = 1$ this is also known as a bundle gerbe with connection.

The higher WZW terms that we are concerned with here are a particular class of Deligne cocycles. Therefore we begin by briefly reviewing Deligne cohomology.

Let $X$ be a smooth manifold and let $\{U_i \to X\}$ be an open cover. Consider then the following double complex.

$$\array{ 0 &\longrightarrow& 0 &\longrightarrow& 0 &\longrightarrow & \cdots \\ \uparrow && \uparrow && \uparrow \\ \Omega^{p+1}(\coprod_i U_i) &\stackrel{\delta}{\longrightarrow}& \Omega^{p+1}(\coprod_{i,j} U_{ i j}) &\stackrel{\delta}{\longrightarrow}& \Omega^{p+1}(\coprod_{i,j, k} U_{i j k}) &\stackrel{\delta}{\longrightarrow}& \cdots \\ \uparrow^{\mathrlap{d}} && \uparrow^{\mathrlap{d}} && \uparrow^{\mathrlap{d}} && \\ \vdots && \vdots && \vdots \\ \uparrow^{\mathrlap{d}} && \uparrow^{\mathrlap{d}} && \uparrow^{\mathrlap{d}} && \\ \Omega^2(\coprod_i U_i) &\stackrel{\delta}{\longrightarrow}& \Omega^2(\coprod_{i,j} U_{ i j}) &\stackrel{\delta}{\longrightarrow}& \Omega^2(\coprod_{i,j, k} U_{i j k}) &\stackrel{\delta}{\longrightarrow}& \cdots \\ \uparrow^{\mathrlap{d}} && \uparrow^{\mathrlap{d}} && \uparrow^{\mathrlap{d}} && \\ \Omega^1(\coprod_i U_i) &\stackrel{\delta}{\longrightarrow}& \Omega^1(\coprod_{i,j} U_{ i j}) &\stackrel{\delta}{\longrightarrow}& \Omega^1(\coprod_{i,j, k} U_{i j k}) &\stackrel{\delta}{\longrightarrow}& \cdots \\ \uparrow^{\mathrlap{d }} && \uparrow^{\mathrlap{d }} && \uparrow^{\mathrlap{d }} && \\ C^\infty(\coprod_i U_i, \mathbb{R}/\mathbb{Z}) &\stackrel{\delta}{\longrightarrow}& C^\infty(\coprod_{i,j} U_{i j}, \mathbb{R}/\mathbb{Z}) &\stackrel{\delta}{\longrightarrow}& C^\infty(\coprod_{i,j,k} U_{i j k}, \mathbb{R}/\mathbb{Z}) &\stackrel{\delta}{\longrightarrow}& \cdots }$$

where vertically we have the de Rham differential and horizontally the Cech differential given by alternating sums of pullback of differential forms.

The corresponding total complex has in degree $n$ the direct sum of the entries in this double complex which are on the $n$th nw-se off-diagonal and has the total differential

$$D = d + (-1)^{deg} \delta$$

with $deg$ denoting form degree. This is the Cech-Deligne complex of $X$.

Example

A Cech-Deligne cocycle in degree $3$ (“bundle gerbe with connection”) is data $(\{\theta_{i}\}, \{A_{i j}\}, \{g_{i j k}\})$ such that

$$\array{ \{\theta_i\} &\stackrel{\delta}{\longrightarrow}& {{\{\theta_j - \theta_i\}} = {d A_{i j}}} && && \\ && \uparrow^{\mathrlap{d}} && && \\ && \{A_{i j}\} &\stackrel{\delta}{\longrightarrow}& \{-A_{ j k} + A_{i k} - A_{i j}\} = \{d g_{i j k}\} && \\ && && \uparrow^{\mathrlap{d }} && \\ && && \{g_{i j k}\} &\stackrel{\delta}{\longrightarrow}& \{g_{j k l} g_{i k l}^{-1} g_{i j l} g_{i j k}^{-1} \} = 1 }$$

Definition

The curvature of a Cech-Deligne cocycle $\overline{\theta} = \{\theta_i, \cdots \}$ is the uniquely defined closed differential $(p+2)$-form $\omega$ such that on all patches

$$\omega|_{U_i} = d \theta_i \,.$$

We also say that $\overline \theta$ is a prequantization of $\omega$.

In the language of sheaf cohomology, Cech-Deligne cohomology of $X$ is equivalently the sheaf hypercohomology with coefficients in the chain complex of abelian sheaves which we denote by

$$\mathbf{B}^{p+1}(\mathbb{R}/\mathbb{Z})_{conn} \coloneqq \left[ \mathbb{Z} \hookrightarrow C^\infty(-,\mathbb{R}) \stackrel{d}{\to} \mathbf{\Omega}^1 \stackrel{d}{\to} \cdots \stackrel{d}{\to} \mathbf{\Omega}^{p+1} \right] \;\;\; \in Sh(SmthMfd, ChainComplexes)[\{quasi\,isomorphisms\}^{-1}] \,.$$

and regard as an object in the derived category over the site of smooth manifolds.

The assignment of curvature is given by the evident morphism of chain complexes of sheaves

$$F_{(-)} \colon \mathbf{B}^{p+1}(\mathbb{R}/\mathbb{Z})_{conn} \longrightarrow \mathbf{\Omega}^{p+2}_{cl}$$

If we then denote a Deligne cocycle as a morphism

$$\overline{\theta} \;\colon\; X \longrightarrow \mathbf{B}^{p+1}(\mathbb{R}/\mathbb{Z})_{conn}$$

in the derived category, then the fact that it prequantizes a form $\omega$ is the statement that there is a commuting diagram (namely in the homotopy theory of smooth higher stacks) of the form

$$\array{ && \mathbf{B}^{p+1}(\mathbb{R}/\mathbb{Z})_{conn} \\ & {}^{\mathllap{\overline{\theta}}}\nearrow & \downarrow \\ X &\stackrel{\omega}{\longrightarrow}& \mathbf{\Omega}^{p+2}_{cl} } \,.$$

The other evident morphism out of the Deligne complex is

$$\chi \colon \mathbf{B}^{p+1}(\mathbb{R}/\mathbb{Z}) \longrightarrow \mathbf{B}^{p+1}(\mathbb{R}/\mathbb{Z}) \,,$$

where on the right we have the complex concentrated on $\mathbb{R}/\mathbb{Z}$ in degree $(p+1)$. Under forming abelian sheaf cohomology this map sends Deligne cocycles to cocycles in ordinary differential cohomology, sometimes called their Dixmier-Douady class.

The key property of the Deligne complex is

Proposition

The Deligne complex is the homotopy fiber product of $\mathbf{B}^{p+1}U(1)$ with $\mathbf{\Omega}^{p+2}_{cl}$ via these two maps:

if we write

$$\flat_{dR}\mathbf{B}^{p+2}(\mathbb{R}) \coloneqq (\mathbf{\Omega}^1 \stackrel{d}{\to}\mathbf{\Omega}^2 \stackrel{d}{\to} \cdots \stackrel{d}{\to} \mathbf{\Omega}^{p+2}_{cl}) then$$

then there is a homotopy pullback diagram of the form

$$\array{ \mathbf{B}^{p+1}(\mathbb{R}/\mathbb{Z})_{conn} &\stackrel{\chi}{\longrightarrow}& \mathbf{B}^{p+1}(\mathbb{R}/\mathbb{Z}) \\ \downarrow^{\mathrlap{F_{(-)}}} && \downarrow \\ \mathbf{\Omega}^{p+2}_{cl} &\stackrel{}{\longrightarrow}& \flat_{dR}\mathbf{B}^{p+1} \mathbb{R}/\mathbb{Z} } \,.$$

For details see around this proposition at Deligne cohomology .

Traditional WZW terms

On Lie groups $G$, those closed $(p+2)$-forms $\omega$ which are left invariant forms may be identified, via the general theory of Chevalley-Eilenberg algebras, with degree $(p+2)$-cocycles $\mu$ in the Lie algebra cohomology of the Lie algebra $\mathfrak{g}$ corresponding to $G$. We have $\omega = \mu(\theta)$where $\theta$ is the Maurer-Cartan form on $G$. These cocycles $\mu$ in turn may arise, via the van Est map, as the Lie differentiation of a degree-$(p+2)$-cocycle $\mathbf{c} \colon \mathbf{B}G \to \mathbf{B}^{p+2}U(1)$ in the Lie group cohomology of $G$ itself, with coefficients in the circle group $U(1)$.

This happens to be the case notably for $G$ a simply connected compact semisimple Lie group such as SU or Spin, where $\mu = \langle -,[-,-]\rangle$, hence $\omega = \langle \theta , [\theta,\theta]\rangle$, is the Lie algebra 3-cocycle in transgression with the Killing form invariant polynomial $\langle -,-\rangle$. This is, up to normalization, a representative of the de Rham image of a generator $\mathbf{c}$ of $H^3(\mathbf{B}G, U(1)) \simeq H^4(B G, \mathbb{Z}) \simeq \mathbb{Z}$.

Generally, by the discussion at geometry of physics – principal bundles, the cocycle $\mathbf{c}$ modulates an infinity-group extension which is a circle p-group-principal infinity-bundle

$$\array{ \mathbf{B}^p U(1) &\longrightarrow& \hat G \\ && \downarrow \\ && G &\stackrel{\Omega\mathbf{c}}{\longrightarrow}& \mathbf{B}^{p+1}U(1) }$$

whose higher Dixmier-Douady class class $\int \Omega \mathbf{c} \in H^{p+2}(X,\mathbb{Z})$ is an integral lift of the real cohomology class encoded by $\omega$ under the de Rham isomorphism. In the example of Spin and $p = 1$ this extension is the string 2-group.

Such a Lie theoretic situation is concisely expressed by a diagram of smooth homotopy types of the form

$$\array{ && &\longrightarrow& \mathbf{B}^{p+1}U(1) \\ &{}^{\mathllap{\Omega \mathbf{c}}}\nearrow& &\swArrow_\simeq& \downarrow^{\mathrlap{\theta_{\mathbf{B}^p U(1)}}} \\ G &\stackrel{\omega}{\longrightarrow}& \mathbf{\Omega}_{cl}^{p+2} &\stackrel{}{\longrightarrow}& \flat_{dR}\mathbf{B}^{p+2}\mathbb{R} } \,,$$

where $\flat_{dR}\mathbf{B}^{p+2}\mathbb{R} \simeq \flat_{dR}\mathbf{B}^{p+2}U(1)$ is the de Rham coefficients (see also at geometry of physics – de Rham coefficients) and where the homotopy filling the diagram is what exhibits $\omega$ as a de Rham representative of $\Omega \mathbf{c}$.

Now, by the very homotopy pullback-characterization of the Deligne complex $\mathbf{B}^{p+1}U(1)_{conn}$ (here), such a diagram is equivalently a prequantization of $\omega$:

$$\array{ && \mathbf{B}^{p+1}U(1)_{conn} &\longrightarrow& \mathbf{B}^{p+1}U(1) \\ &{}^\mathllap{\nabla}\nearrow& \downarrow &\swArrow_\simeq& \downarrow^{\mathrlap{\theta_{\mathbf{B}^p U(1)}}} \\ G &\stackrel{\omega}{\longrightarrow}& \mathbf{\Omega}_{cl}^{p+2} &\stackrel{}{\longrightarrow}& \flat_{dR}\mathbf{B}^{p+2}\mathbb{R} } \,.$$

For $\omega = \langle -,[-,-]\rangle$ as above, we have $p= 1$ and so $\nabla$ here is a circle 2-bundle with connection, often referred to as a bundle gerbe with connection. As such, this is also known as the WZW gerbe or similar.

This terminology arises as follows. In (Wess-Zumino 84) the sigma-model for a string propagating on the Lie group $G$ was considered, with only the standard kinetic action term. Then in (Witten 84) it was observed that for this action functional to give a conformal field theory after quantization, a certain higher gauge interaction term has to the added. The resulting sigma-model came to be known as the Wess-Zumino-Witten model or WZW model for short, and the term that Witten added became the WZW term. In terms of string theory it describes the propagation of the string on the group $G$ subject to a force of gravity given by the Killing form Riemannian metric and subject to a B-field higher gauge force whose field strength is $\omega$. In (Gawedzki 87) it was observed that when formulated properly and generally, this WZW term is the surface holonomy functional of a connection on a bundle gerbe $\nabla$ on $G$. This is equivalently the $\nabla$ that we just motivated above.

Later, such WZW terms, or at least their curvature forms $\omega$, were recognized all over the place in quantum field theory. For instance the Green-Schwarz sigma-models for super p-branes each have an action functional that is the sum of the standard kinetic action plus a WZW term of degree $p+2$.

In general WZW terms are “gauged” which means, as we will see, that they are not defined on the given smooth infinity-group $G$ itself, but on a bundle $\tilde G$ of differential moduli stacks over that group, such that a map $\Sigma \to \tilde G$ is a pair consisting of a map $\Sigma \to G$ and of a higher gauge field on $\Sigma$ (a “tensor multiplet” of fields).

Here we discuss the general construction and theory of such higher WZW terms.

$L_\infty$-algebras

For $V$ a graded vector space, for $v_i \in V_{\vert v_i\vert}$ homogenously graded elements, and for $\sigma$ a permutation of $n$ elements, write $\chi(\sigma, v_1, \cdots, v_n)\in \{-1,+1\}$ for the product of the signature of the permutation with a factor of $(-1)^{\vert v_i \vert \vert v_j \vert}$ for each interchange of neighbours $(\cdots v_i,v_j, \cdots )$ to $(\cdots v_j,v_i, \cdots )$ involved in the permutation.

Definition

An L-∞ algebra is

1. a graded vector space $V$;

2. for each $n \in \mathbb{N}$ a multilinear map called the $n$-ary bracket

   $l_n(\cdots) \coloneqq [-,-, \cdots, -] \colon V^{\wedge n} \to V$

   of degree $n-2$

such that

1. each $l_n$ is graded antisymmetric, in that for every permutation $\sigma$ and homogeneously graded elements $v_i \in V_{\vert v_i \vert}$ then

   $$l_n(v_{\sigma(1)}, v_{\sigma(2)},\cdots ,v_{\sigma(n)}) = \chi(\sigma,v_1,\cdots, v_n) \cdot l_n(v_1, v_2, \cdots v_n)$$

2. the generalized Jacobi identity holds:

   (1)$$\sum_{i+j = n+1} \sum_{\sigma \in UnShuff(i,n-i)} \chi(\sigma,v_1, \cdots, v_m) (-1)^{i(j-1)} l_{j} \left( l_i \left( v_{\sigma(1)}, \cdots, v_{\sigma(i)} \right), v_{\sigma(i+1)} , \cdots , v_{\sigma(n)} \right) = 0 \,,$$

   for all $n$, all and homogeneously graded elements $v_i \in V_i$ (here the inner sum runs over all $(i,j)$-unshuffles $\sigma$).

There are various different conventions on the gradings possible, which lead to similar formulas with different signs.

Example

In lowest degrees the generalized Jacobi identity says that

1. for $n = 1$: the unary map $\partial \coloneqq l_1$ squares to 0:

   $$\partial (\partial(v_1)) = 0$$

1: for $n = 2$: the unary map $\partial$ is a graded derivation of the binary map

$$- [\partial v_1, v_2] - (-1)^{\vert v_1 \vert \vert v_2 \vert} [\partial v_2, v_1] + \partial [v_1, v_2] = 0$$

hence

$$\partial [v_1, v_2] = [\partial v_1, v_2] + (-1)^{\vert v_1 \vert}[v_1, \partial v_2] \,.$$

Example

When all higher brackets vanish, $l_{k \gt 2}= 0$ then for $n = 3$:

$$[[v_1,v_2],v_3] + (-1)^{\vert v_1 \vert (\vert v_2 \vert + \vert v_3 \vert)} [[v_2,v_3],v_1] + (-1)^{\vert v_2 \vert (\vert v_1 \vert + \vert v_3 \vert)} [[v_1,v_3],v_2] = 0$$

this is the graded Jacobi identity. So in this case the $L_\infty$-algebra is equivalently a dg-Lie algebra.

Example

When $l_3$ is possibly non-vanishing, then on elements $x_i$ on which $\partial = l_1$ vanishes then the generalized Jacobi identity for $n = 3$ gives

$$[[v_1,v_2],v_3] + (-1)^{\vert v_1 \vert (\vert v_2 \vert + \vert v_3 \vert)} [[v_2,v_3],v_1] + (-1)^{\vert v_2 \vert (\vert v_1 \vert + \vert v_3 \vert)} [[v_1,v_3],v_2] = - \partial [v_1, v_2, v_3] \,.$$

This shows that the Jacobi identity holds up to an “exact” term, hence up to homotopy.

Assume now for simplicity that $V$ is degreewise finite dimensional, Write $V^\ast$ for its degreewise dual.

Definition

Given an L-∞ algebra $\mathfrak{g}$, def. , which is is finite type (in that it is degreewise finite dimensional) its Chevalley-Eilenberg algebra $CE(\mathfrak{g})$ is the dg-algebra

$$CE(\mathfrak{g}) = (\wedge^\bullet V^\ast, d_{CE})$$

whose underlying graded algebra is the graded Grassmann algebra on $V^\ast$, hence the graded-symmetric algebra on $V^\ast[-1]$, and whose differential is given on generators co-component-wise by the linear dual of the higher brackets:

$$(d_{CE})_n \coloneqq l_n^\ast \colon V \stackrel{d_{CE}}{\longrightarrow} \wedge^\bullet V^\ast \stackrel{p}{\to} \wedge^n V^\ast \,.$$

Propositon

The construction of def. constitutes a full and faithful functor

$$CE(-) \;\colon\; L_\infty Alg_{ft} \longrightarrow dgAlg^{op}$$

from $L_\infty$-algebras of finite type whose essential image consists of those dg-algebras whose underlyoing graded algebra is free graded-commutative, i.e. a graded Grassmann algebra.

Using this proposition, it is often more convenient to reason with the CE-algebras than with the $L_\infty$-algebras directly.

Proposition

On connective $L_\infty$-algebras (those whose underlying chain complex is concentrated in non-negative degrees), passage to degree-0 chain homology constitutes a functor (“0-truncation”) to plain Lie algebras

$$\tau_0 \coloneqq H^0 \colon L_\infty Alg_{\geq 0} \longrightarrow LieAlg \,.$$

Higher Poisson brackets

Poisson brackets and Heisenberg algebra

We discuss the traditional definition of the Poisson bracket of a (pre-)symplectic manifold, highlighting how conceptually it may be understood as the algebra of infinitesimal symmetries of any of its prequantizations.

Definition

Let $X$ be a smooth manifold. A closed differential 2-form $\omega \in \Omega_{cl}^2(X)$ is a symplectic form if it is non-degenerate in that the kernel of the operation of contracting with vector fields

$$\iota_{(-)}\omega \colon Vect(X) \longrightarrow \Omega^1(X)$$

is trivial: $ker(\iota_{(-)}\omega) = 0$.

If $\omega$ is just closed with possibly non-trivial kernel, we call it a presymplectic form. (We do not require here the dimension of the kernel restricted to each tangent space to be constant.)

Definition

Given a presymplectic manifold $(X, \omega)$, then a Hamiltonian for a vector field $v \in Vect(X)$ is a smooth function $H \in C^\infty(X)$ such that

$$\iota_{v} \omega + d H = 0 \,.$$

If $v \in Vect(X)$ is such that there exists at least one Hamiltonian for it then it is called a Hamiltonian vector field. Write

$$HamVect(X,\omega) \hookrightarrow Vect(X)$$

for the $\mathbb{R}$-linear subspace of Hamiltonian vector fields among all vector fields

Remark

When $\omega$ is symplectic then, evidently, there is a unique Hamiltonian vector field, def. , associated with every Hamiltonian, i.e. every smooth function is then the Hamiltonian of precisely one Hamiltonian vector field (but two different Hamiltonians may still have the same Hamiltonian vector field uniquely associated with them). As far as prequantum geometry is concerned, this is all that the non-degeneracy condition that makes a closed 2-form be symplectic is for. But we will see that the definitions of Poisson brackets and of quantomorphism groups directly generalize also to the presymplectic situation, simply by considering not just Hamiltonian fuctions but pairs of a Hamiltonian vector field and a compatible Hamiltonian.

Definition

Let $(X,\omega)$ be a presymplectic manifold. Write

$$Ham(X,\omega) \hookrightarrow HamVect(X,\omega) \oplus C^\infty(X)$$

for the linear subspace of the direct sum of Hamiltonian vector fields, def. , and smooth functions on those pairs $(v,H)$ for which $H$ is a Hamiltonian for $v$

$$Ham(X,\omega) \coloneqq \left\{ (v,H) | \iota_v \omega + d H = 0 \right\} \,.$$

Define a bilinear map

$$[-,-] \;\colon\; Ham(X,\omega) \otimes Ham(X,\omega) \longrightarrow Ham(X,\omega)$$

by

$$[(v_1,H_1), (v_2,H_2)] \coloneqq ([v_1,v_2], \iota_{v_2}\iota_{v_1} \omega) \,,$$

called the Poisson bracket, where $[v_1,v_2]$ is the standard Lie bracket on vector fields. Write

$$\mathfrak{poiss}(X,\omega) \coloneqq (Ham(X,\omega),[-,-])$$

for the resulting Lie algebra. In the case that $\omega$ is symplectic, then $Ham(X,\omega) \simeq C^\infty(X)$ and hence in this case

$$\mathfrak{poiss}(X,\omega) \simeq (C^\infty(X),[-,-]) \,.$$

Example

Let $X = \mathbb{R}^{2n}$ and let $\omega = \sum_{i = 1}^n d p_i \wedge d q^i$ for $\{q^i\}_{i = 1}^n$ the canonical coordinates on one copy of $\mathbb{R}^n$ and $\{p_i\}_{i = 1}^n$ that on the other (“canonical momenta”). Hence let $(X,\omega)$ be a symplectic vector space of dimension $2n$, regarded as a symplectic manifold.

Then $Vect(X)$ is spanned over $C^\infty(X)$ by the canonical bases vector fields $\{\partial_{q^i}, \partial_{p^i}\}$. These basis vector fields are manifestly Hamiltonian vector fields via

$$\iota_{\partial_{q^i}} \omega = - d p_i$$

$$\iota_{\partial_{p_i}} \omega = + d q^i \,.$$

Moreover, since $X$ is connected, these Hamiltonians are unique up to a choice of constant function. Write $\mathbf{i} \in C^\infty(X)$ for the unit constant function, then the nontrivial Poisson brackets between the basis vector fields are

$$[q^i, p_j] \coloneqq [(-\partial_{p_i}, q^i), (\partial_{q^j}, p_j)] = - \delta_j^i (0, \mathbf{i}) = - \delta_j^i \mathbf{i} \,.$$

This is called the Heisenberg algebra.

More generally, the Hamiltonian vector fields corresponding to quadratic Hamiltonians, i.e. degree-2 polynomials in the $\{q^i\}$ and $\{p_i\}$, generate the affine symplectic group of $(X,\omega)$. The freedom to add constant terms to Hamiltonians gives the extended affine symplectic group.

Infinitesimal quantomorphisms

Example serves to motivate a more conceptual origin of the definition of the Poisson bracket in def. .

Example

Write

$$\theta \coloneqq \sum_{i = 1}^n p_i d q_i \in \Omega^1(\mathbb{R}^{2n})$$

for the canonical choice of differential 1-form satisfying

$$d \theta = \omega \,.$$

If we regard $\mathbb{R}^{2n} \simeq T^\ast \mathbb{R}^n$ as the cotangent bundle of the Cartesian space $\mathbb{R}^n$, then this is what is known as the Liouville-Poincaré 1-form.

Since $\mathbb{R}^{2n}$ is contractible as a topological space, every circle bundle over it is necessarily trivial, and hence any choice of 1-form such as $\theta$ may canonically be thought of as being a connection on the trivial $U(1)$-principal bundle. As such this $\theta$ is a prequantization of $(\mathbb{R}^{2n}, \sum_{i=1}^n d p_i \wedge d q^i)$.

Being thus a circle bundle with connection, $\theta$ has more symmetry than its curvature $\omega$ has: for $\alpha \in C^\infty(\mathbb{R}^{2n}, U(1))$ any smooth function, then

$$\theta \mapsto \theta + d\alpha$$

is the gauge transformation of $\theta$, leading to a different but equivalent prequantization of $\omega$.

Hence while a vector field $v$ is said to preserve $\omega$ (is a symplectic vector field) if the Lie derivative of $\omega$ along $v$ vanishes

$$\mathcal{L}_v \omega = 0$$

in the presence of a choice for $\theta$ the right condition to ask for is that there is $\alpha$ such that

$$\mathcal{L}_v \theta = d \alpha \,.$$

For more on this see also at prequantized Lagrangian correspondence.

Notice then the following basic but important fact.

Proposition

For $(X,\omega)$ a presymplectic manifold and $\theta \in \Omega^1(X)$ a 1-form such that $d \theta = \omega$ then for $(v,\alpha) \in Vect(X)\oplus C^\infty(X)$ the condition $\mathcal{L}_v \theta = d \alpha$ is equivalent to the condition that makes

$$H \coloneqq \iota_v \theta - \alpha$$

a Hamiltonian for $v$ according to def. :

$$\mathcal{L}_v \theta = d \alpha \;\;\;\Leftrightarrow\;\;\; \iota_v \omega + d (\underset{H}{\underbrace{\iota_v \theta - \alpha}}) = 0 \,.$$

Moreover, the Poisson bracket, def. , between two such Hamiltonian pairs $(v_i, \alpha_i -\iota_v \theta)$ is equivalently given by the skew-symmetric Lie derivative of the corresponding vector fields on the $\alpha_i$:

(2)$$\iota_{[v_1,v_2]} \theta - \iota_{v_2}\iota_{v_1}\omega = \mathcal{L}_{v_1} \alpha_2 - \mathcal{L}_{v_2} \alpha_1$$

Proof

Using Cartan's magic formula and by the prequantization condition $d \theta = \omega$ the we have

$$\begin{aligned} \mathcal{L}_v \theta &= \iota_v d\theta + d \iota_v \theta \\ & = \iota_v\omega + d \iota_v \theta \end{aligned} \,.$$

This gives the first statement. For the second we first use the formula for the de Rham differential and then again the definition of the $\alpha_i$

$$\begin{aligned} \iota_{v_2}\iota_{v_1} \omega & = \iota_{v_2}\iota_{v_1} d\theta \\ & = \iota_{v_1} d \iota_{v_2} \theta - \iota_{v_2} d \iota_{v_1} \theta - \iota_{[v_1,v_2]} \theta \\ & = \iota_{v_1} d \alpha_2 - \iota_{v_1} \iota_{v_2}\omega - \iota_{v_2} d \alpha_1 + \iota_{v_2} \iota_{v_1}\omega - \iota_{[v_1,v_2]} \theta \\ & = 2 \iota_{v_2} \iota_{v_1}\omega + \mathcal{L}_{v_1} \alpha_2 -\mathcal{L}_{v_2} \alpha_1 - \iota_{[v_1,v_2]} \theta \end{aligned} \,.$$

Corollary

For $(X,\omega)$ a presymplectic manifold with $\theta \in \Omega^1(X)$ such that $d \theta = \omega$, consider the Lie algebra

$$\mathfrak{quantmorph}(X,\theta) = \left\{ (v,\alpha) | \mathcal{L}_v \theta = d \alpha \right\} \subset Vect(X) \oplus C^\infty(X)$$

with Lie bracket

$$[(v_1,\alpha_1), (v_2,\alpha_2)] = ([v_1,v_2], \mathcal{L}_{v_1}\alpha_2 - \mathcal{L}_{v_2}\alpha_1) \,.$$

Then by (2) the linear map

$$(v,H) \mapsto (v, \iota_v \theta - H)$$

is an isomorphism of Lie algebras

$$\mathfrak{poiss}(X,\omega) \stackrel{\simeq}{\longrightarrow} \mathfrak{quantmorph}(X,\theta)$$

from the Poisson bracket Lie algebra, def. .

This shows that for exact pre-symplectic forms the Poisson bracket Lie algebra is secretly the Lie algebra of infinitesimal symmetries of any of its prequantizations. In fact this holds true also when the pre-symplectic form is not exact:

Definition

For $(X,\omega)$ a presymplectic manifold, a Cech-Deligne cocycle

$$(X,\overline{\theta}) \coloneqq (X,\{U_i\},\{g_{i j}, \theta_i\})$$

for a prequantization of $(X,\omega)$ is

1. an open cover $\{U_i \to X\}_i$;

2. 1-forms $\{\theta_i \in \Omega^1(U_i)\}$;

3. smooth function $\{g_{i j} \in C^\infty(U_{i j}, U(1))\}$

such that

1. $d \theta_i = \omega|_{U_i}$ on all $U_i$;

2. $\theta_j = \theta_i + d log g_{ij}$ on all $U_{i j}$;

3. $g_{i j} g_{j k} = g_{i k}$ on all $U_{i j k}$.

The quantomorphism Lie algebra of $\overline{\theta}$ is

$$\mathfrak{quantmorph}(X,\overline{\theta}) = \left\{ (v, \{\alpha_i\}) | \mathcal{L}_v log g_{i j} = \alpha_j - \alpha_i \,, \mathcal{L}_v \theta_i = d \alpha_i \right\} \subset Vect(X) \oplus \left(\underset{i}{\bigoplus} C^\infty(U_i)\right)$$

with bracket

$$[(v_1, \{(\alpha_1)_i\}), (v_2, \{(\alpha_2)_i\})] \coloneqq ([v_1,v_2], \{\mathcal{L}_{v_1}(\alpha_2)_i - \mathcal{L}_{v_2} (\alpha_1)_i\}) \,.$$

Proposition

For $(X,\omega)$ a presymplectic manifold and $(X,\{U_i\},\{g_{i j}, \theta_i\})$ a prequantization, def. , the linear map

$$(v,H) \mapsto (v, \{\iota_v \theta_i - H|_{U_i}\})$$

constitutes an isomorphism of Lie algebras

$$\mathfrak{poiss}(X,\omega) \stackrel{\simeq}{\longrightarrow} \mathfrak{quantmorph}(X,\overline{\theta})$$

between the Poisson bracket algebra of def. and that of infinitesimal quantomorphisms, def. .

Proof

The condition $\mathcal{L}_v log g_{i j} = \alpha_j - \alpha_i$ on the infinitesimal quantomorphisms, together with the Cech-Deligne cocycle condition $d log g_{i j} = \theta_j - \theta_i$ says that on $U_{i j}$

$$\iota_v \theta_j - \alpha_j = \iota_v \theta_i - \alpha_i$$

and hence that there is a globally defined function $H \in C^\infty(X)$ such that $\iota_v \theta_i - \alpha_i = H|_{U_i}$. This shows that the map is an isomrophism of vector spaces.

Now over each $U_i$ the the situation for the brackets is just that of corollary implied by (2), hence the morphism is a Lie homomorphism.

The Kostant-Souriau extension

The following fact is immediate, but important.

Proposition

Given a presymplectic manifold $(X,\omega)$, then the Poisson bracket Lie algebra $\mathfrak{poiss}(X,\omega)$, def. , is a central Lie algebra extension of the algebra of Hamiltonian vector fields, def. , by the degree-0 de Rham cohomology group of $X$: there is a short exact sequence of Lie algebras

$$0 \to H^0(X) \stackrel{}{\longrightarrow} \mathfrak{poiss}(X,\omega) \stackrel{}{\longrightarrow} HamVect(X,\omega) \to 0 \,.$$

Hence when $X$ is connected, then $\mathfrak{poiss}(X,\omega)$ is an $\mathbb{R}$-extension of the Hamiltonian vector fields:

$$0 \to \mathbb{R} \stackrel{}{\longrightarrow} \mathfrak{poiss}(X,\omega) \stackrel{}{\longrightarrow} HamVect(X,\omega) \to 0 \,.$$

Moreover, given any choice of splitting of the underlying short exact sequence of vector spaces as $\mathfrak{pois}(X,\omega) \simeq_{vs} HamVect(X,\omega)\oplus H^0(X)$, which is equivalently a choice of Hamitlonian $H_v$ for each Hamiltonian vector field $v$, the Lie algebra cohomology 2-cocycle which classifies this extension is

$$(v_1, v_2) = \iota_{v_2}\iota_{v_1}\omega - H_{[v_1,v_2]} \,.$$

Proof

The morphism $\mathfrak{poiss}(X,\omega) \to HamVect(X,\omega)$ is on elements given just by projection onto the direct summand of vector fields, taking a Hamiltonian pair $(v,H)$ to $v$. This is surjective by the very definition of $HamVect(X,\omega)$, in fact $HamVect(X,\omega)$ is the image of this map regarded as a morphism $\mathfrak{poiss}(X,\omega) \longrightarrow Vect(X)$. Moreover, the kernel of this projection is manifestly the space of Hamiltonian pairs of the form $(v = 0,H)$. By the defining constraint $\iota_v \omega = d H$ these are precisely the pairs for which $d H = 0$. This gives the short exact sequence as stated.

Generally, given a Lie algebra $\mathfrak{g}$ and an $\mathbb{R}$-valued 2-cocycle $\mu_2$ in Lie algebra cohomology, then the Lie algebra extension that it classifies is $\hat \mathfrak{g} =_{vs} \mathfrak{g}\oplus \mathbb{R}$ with bracket

$$[(x_1,a_1), (x_2,x_2)] = ([x_1,x_2], \mu_2(a_1,a_2)) \,.$$

Applied to the case at hand, given a choice of splitting $v\mapsto (v,H_v)$ this yields

$$[(v_1,H_{v_1} + a_1), (v_2, H_{v_2} + a_2) ] = ([v_1,v_2], H_{[v_1,v_2]} + \iota_{v_2}\iota_{v_1}\omega - H_{[v_1,v_2]}) = ([v_1,v_2], \iota_{v_2}\iota_{v_1}\omega ) \,.$$

Example

Consider again example where $(X,\omega) = (\mathbb{R}^{2n}, d p_i \wedge d q^i)$ is a symplectic vector space and where we restrict along the inclusion of the translation vector fields to get the Heisenberg algebra. Then the KS-extension of prop. also pulls back:

$$\array{ H_{dR}^0(X) &\longrightarrow& H_{dR}^0(X) \\ \downarrow && \downarrow \\ \mathfrak{heis}(X,\omega) &\longrightarrow& \mathfrak{poiss}(X,\omega) \\ \downarrow && \downarrow \\ \mathbb{R}^{2 n} &\longrightarrow& HamVect(X,\omega) } \,.$$

The Lie algebra cohomology 2-cocycle which classifiesthe Kostant-Souriau extension, $\iota_{(-)}\iota_{(-)}\omega$ manifestly restricts to the Heisenberg cocycle $(q^i, p_j) = \delta^i_j$.

Higher Poisson brackets and higher Heisenberg algebra

In the discussion above we amplified that the definition of the Poisson bracket of a symplectic form has an immediate generalization to presymplectic forms, hence to any closed differential 2-form. This naturally suggests to ask for higher analogs of this bracket for the case of of closed differential (p+2)-forms $\omega \in \Omega^{p+2}(X)$ for $p \gt 0$.

Indeed, the natural algebraic form of definition of Hamiltonian vector fields makes immediate sense for higher $p$, with the Hamiltonians $H$ now being $p$-forms, and the natural algebraic form of the binary Poisson bracket of def. makes immediate sense as a bilinear pairing for any $p$:

$$[(v_1, H_1), (v_2, H_2)] \coloneqq ([v_1,v_2], \iota_{v_2} \iota_{v_1} \omega) \,.$$

However, one finds that for $p \gt 0$ then this bracket does not satisfy the Jacobi identity. On the other hand, the failure of the Jacobi identity turns out to be an exact form, and hence in the spirit of regarding the shift of a differential form by a de Rham differential as a homotopy or gauge transformation this suggests that the bracket might still give a Lie algebra upto higher coherent homotopy, called a strong homotopy Lie algebra or L-∞ algebra. This turns out to indeed be the case (n-plectic+geometry#Rogers 10).

Definition

For $p \in \mathbb{N}$, we say that a pre-(p+1)-plectic manifold is a smooth manifold $X$ equipped with a closed degree-$(p+2)$ differential form $\omega \in \Omega^{p+2}(X)$.

This is called an (p+1)-plectic manifold if the kernel of the contraction map

$$\iota_{(-)} \colon Vect(X) \longrightarrow \Omega^{p+1}(X)$$

is trivial.

Definition

Given a pre-$(p+1)$-plectic manifold $(X,\omega)$, def. , write

$$Ham^{p}(X) \subset Vect(X) \oplus \Omega^{p}(X)$$

for the subspace of the direct sum of vector fields $v$ on $X$ and differential p-forms $J$ on $X$ satisfying

$$\iota_v \omega + d J = 0 \,.$$

We call these the pairs of Hamiltonian forms with their Hamiltonian vector fields.

Definition

Given a pre-$(p+1)$-plectic manifold $(X,\omega)$, def. , define an L-∞ algebra $\mathfrak{poiss}(X,\omega)$, to be called the Poisson bracket Lie (p+1)-algebra as follows.

The underlying chain complex is the truncated de Rham complex ending in Hamiltonian forms as in def. :

$$\Omega^0(X) \stackrel{d}{\to} \Omega^1(X) \stackrel{d}{\to} \cdots \stackrel{d}{\to} \Omega^{p-1}(X) \stackrel{(0,d)}{\longrightarrow} Ham^{p}(X)$$

with the Hamiltonian pairs, def. , in degree 0 and with the 0-forms (smooth functions) in degree $p$.

The non-vanishing $L_\infty$-brackets are defined to be the following

• $l_1(J) = d J$

• $l_{k \geq 2}(v_1 + J_1, \cdots, v_k + J_k) \coloneqq - (-1)^{\left(k+1 \atop 2\right)} \iota_{v_k}\cdots \iota_{v_1}\omega$.

Proposition

Definition indeed gives an L-∞ algebra in that the higher Jacobi identity is satisfied.

(3)$$\sum_{i+j = n+1} \sum_{\sigma \in UnShuff(i,j)} (-1)^{sgn(\sigma)} l_i \left( l_j \left( x_{\sigma(1)}, \cdots, x_{\sigma(j)} \right), x_{\sigma(j+1)} , \cdots , x_{\sigma(n)} \right) = 0 \,,$$

For the special case of $(p+1)$-plectic $\omega$, prop. is due to (Rogers 10, lemma 3.7), for the general pre-$(p+1)$-plectic case this is (FRS 13b, prop. 3.1.2).

Proof

Repeatedly apply Cartan's magic formula $\mathcal{L}_v = \iota_v \circ d + d \circ \iota_v$ as well as the consequence $\mathcal{L}_{v_1} \circ \iota_{v_2} - \iota_{v_2} \circ \mathcal{L}_{v_1} = \iota_{[v_1,v_2]}$ to find that for all vector fields $v_i$ and differential forms $\beta$ (of any degree, not necessarily closed) one has

$$\begin{aligned} (-1)^k d \iota_{v_k} \cdots \iota_{v_1} \beta = & \underset{1 \leq i \lt j \leq k}{\sum} (-1)^{i+j} \iota_{v_k} \cdots \widehat{\iota_{v_j}} \cdots \widehat{\iota_{v_i}} \cdots \iota_{[v_i,v_j]} \\ & + \underoverset{i=1}{k}{\sum} (-1)^i \iota_{v_k} \cdots \widehat{\iota_{v_i}} \cdots \iota_{v_1} \mathcal{L}_{v_i} \beta \\ & + \iota_{v_k} \cdots \iota_{v_1} d \beta \end{aligned} \,.$$

With this, the statement follows straightforwardly.

Higher infinitesimal quantomorphisms and conserved currents

There is an evident generalization of the prequantization, def. , of closed 2-forms by circle bundles with connection, hence by degree-2 cocycles in Deligne cohomology, to the prequantization of closed $(p+2)$-forms by degree-$(p+2)$-cocycles in Deligne cohomology.

Definition

Given a pre-(p+1)-plectic manifold $(X,\omega)$, then a prequantization is a Cech-Deligne cocycle $\overline{\theta}$, the prequantum (p+1)-bundle, whose curvature, def. , equals $\omega$:

$$F_{\overline{\theta}} = \omega \,.$$

Remark

In terms of diagrams in the homotopy theory $\mathbf{H}$ of smooth homotopy types, def. describes lifts of the form

$$\array{ && \mathbf{B}^{p+1}U(1)_{conn} \\ & {}^{\mathllap{\overline{\theta}}}\nearrow & \downarrow^{\mathrlap{F_{(-)}}} \\ X &\stackrel{\omega}{\longrightarrow} & \mathbf{\Omega}^{p+2}_{cl} } \,.$$

This way there is an immediate generalization of def. to forms and cocycles of higher degree:

Definition

Let $\overline{\theta}$ be any Cech-Deligne-cocycle relative to an open cover $\mathcal{U}$ of $X$, which gives a prequantum n-bundle for $\omega$. The L-∞ algebra $\mathfrak{quantmorph}(X,\overline{\theta})$ is the dg-Lie algebra (regarded as an $L_\infty$-algebra) whose underlying chain complex is the Cech total complex made to end in Hamiltonian Cech cocycles

• $\mathfrak{quantmorph}(X,\overline{\theta})^0 \coloneqq \{v+ \overline{\alpha} \in Vect(X)\oplus Tot^{n-1}(\mathcal{U}, \Omega^\bullet) \;\vert\; \mathcal{L}_v \overline{\theta} = \mathbf{d}_{Tot}\overline{\alpha}\}$;

• $\mathfrak{quantmorph}(X,\overline{\theta})^{i \gt 0} \coloneqq C^{n-1-i}(\mathcal{U},\Omega^\bullet)$

with differential given by $d_{tot} = d + (-1)^{deg} \delta$.

The non-vanishing dg-Lie brackets on this complex are given by the evident action of vector fields on all the components of the Cech cochains by Lie derivative:

• $[v_1 + \overline{\alpha}_1, v_2 + \overline{\alpha}_2] \coloneqq [v_1, v_2] + \mathcal{L}_{v_1}\overline{\alpha}_2 - \mathcal{L}_{v_2}\overline{\alpha}_1$

• $[v+ \overline{\alpha}, \overline{\eta}] = - [\overline{\eta}, v + \overline{\alpha}] = \mathcal{L}_v \overline{\eta}$.

(FRS 13b, def./prop. 4.2.1)

One then finds a direct higher analog of corollary (its proof however is requires a bit more work):

Proposition

There is an equivalence in the homotopy theory of L-∞ algebras

$$f \colon \mathfrak{poiss}(X,\omega) \stackrel{\simeq}{\longrightarrow} \mathfrak{quantmorph}(X,\overline{\theta})$$

between the $L_\infty$-algebras of def. and def. (in particular def. does not depend on the choice of $\overline{A}$) whose underlying chain map satisfies

• $f(v + J) = (v,\; \sum_{i = 0}^n (-1)^i \iota_v \theta^{n-i} - J|_{\mathcal{U}})$.

(FRS 13b, theorem 4.2.2)

Remark

Proposition says that all the higher Poisson $L_\infty$-algebras are $L_\infty$-algebras of symmetries of Deligne cocycles prequantizing the give pre-$(p+1)$-plectic form, higher “quantomorphisms”.

In fact the dg-algebra $\mathfrak{quantmorph}(X,\overline{\theta})$ makes yet another equivalent interpretation of $\mathfrak{poiss}(X,\omega)$ manifest: it is also a resolution of the Dickey bracket of conserved currents for WZW sigma-models. This we come to below.

Higher Kostant-Souriau extension

The higher Poisson brackets come with a higher analog of the Kostant-Souriau extension, prop. .

Definition

Write

$$\mathbf{H}(X,\flat \mathbf{B}^p \mathbb{R}) \coloneqq (\Omega^0(X) \stackrel{d}{\to} \Omega^1(X) \stackrel{d}{\to} \cdots \Omega^{(p-1)}(X) \stackrel{d}{\to}\Omega^p_{cl}(X))$$

for the truncated de Rham complex regarded as an abelian L-∞ algebra.

Proposition

Given a pre-(p+1)-plectic manifold $(X,\omega)$,

the Poisson bracket Lie (p+1)-algebra $\mathfrak{poiss}(X,\omega)$, def. , is an L-∞ extension of the Hamiltonian vector fields by the truncated de Rham complex, def. , there is a homotopy fiber sequence of $L_\infty$-algebras of the form

$$\array{ \mathbf{H}(X,\flat\mathbf{B}^p \mathbb{R}) &\longrightarrow& \mathfrak{poiss}(X,\omega) &\longrightarrow& HamVect(X,\omega) \\ && && \downarrow^{\mathrlap{\iota_{\cdots}\omega} } \\ && && \mathbf{B} \mathbf{H}(X,\flat \mathbf{B}^p \mathbb{R}) } \,.$$

(FRS 13b, theorem 3.3.1)

To better see what this means, we may truncate this down to a statement about ordinary Lie algebras.

Proposition

Given a pre-(p+1)-plectic manifold $(X,\omega)$, the 0-truncation, prop. , of the higher Kostant-Souriau extension of prop. is a Lie algebra extension of the Hamiltonian vector fields by the de Rham cohomology group $H^p(X)$.

$$0 \to H^p(X) \longrightarrow \tau_0 \mathfrak{poiss}(X,\omega) \longrightarrow HamVect(X,\omega) \to 0 \,.$$

Session II

We recall how Lie integration sends L-∞ algebras $\mathfrak{g}$ to higher smooth group stacks (smooth ∞-groups) $G$ and then discuss how every L-∞ cocycle Lie integrates to a Deligne cocycle on a differential extension $\tilde G$ of $G$ – these are higher WZW terms. As an example we consider the collection of $L_\infty$-cocycles on the super translation Lie algebra and its higher extensions.

For this purpose we need to pass (along the Dold-Kan correspondence) from the abelian derived category over the site of smooth manifolds to the “nonabelian derived category”, by generalizing chain complexes to Kan complexes and generally to simplicial sets. Therefore we now consider simplicial presheaves over the site of smooth Cartesian spaces localized at the local (i.e. stalk-wise) weak homotopy equivalences as models for higher smooth stacks

$$L_{lqi} PSh(CartSp, Ch_{\bullet \geeq 0}) \stackrel{DK}{\longrightarrow} L_{lwhe} PSh(CartSp, sSet) =: Smooth\infty Grpd$$

We assume here a working familiarity with at least the basic idea of such a setup for higher differential geometry, for details see geometry of physics – smooth homotopy types.

$L_\infty$-algebra cohomology and Rational homotopy theory

Rationally, what we are going to be concerned with is all enoced in L-∞ algebra cohomology for super L-∞ algebras. We briefly recall this, following (Sati-Schreiber-Stasheff 09). For more exposition see at super Cartan geometry. All algebras here are over $\mathbb{R}$.

Recall the dg-algebraic perspective on $L_\infty$-algebras of finite type from prop. .

First of all the operation of sending finite dimensional Lie algebras to their Chevalley-Eilenberg algebras is a fully faithful functor

$$\begin{aligned} LieAlg &\stackrel{}{\hookrightarrow} dgAlg^{op} \\ (\mathfrak{g}, [-,-]) & \mapsto CE(\mathfrak{g}) \coloneqq (\wedge \mathfrak{g}^\ast, d_{CE} = [-,-]^\ast) \end{aligned}$$

from the category of Lie algebras to the opposite category of dg-algebras.

Generalizing the image of this functor to those dg-algebras of the form $(\wedge^\bullet \mathfrak{g}^\ast, d)$ for $\mathfrak{g}$ an $\mathbb{N}$-graded vector space of finite type yields the opposite of the category of (connective) L-∞ algebras of finite type:

$$\begin{aligned} L_\infty Alg & \hookrightarrow dgAlg^{op} \\ (\mathfrak{g}, [-], [-,-], [-,-,-], \cdots) & \mapsto CE(\mathfrak{g}) \coloneqq (\wedge \mathfrak{g}^\ast, d_{CE} = [-]^\ast + [-,-]^\ast + [-,-,-]^\ast + \cdots) \end{aligned} \,.$$

Accordingly, super L-∞ algebras are given by generalizing this further to $\mathfrak{g}$ being an $\mathbb{N}$-graded super vector space of finite type and regarding the Grassmann algebra $\wedge^\bullet \mathfrak{g}^\ast$ as $(\mathbb{Z},\mathbb{Z}_2)$-bigraded (see at signs in supergeometry).

$$CE \colon sL_\infty Alg \hookrightarrow sdgAlg^{op} \,.$$

Proposition

The category $sL_\infty Alg$ carries a canonical stucture of a category of fibrant objects whose

• weak equivalences are the morphisms that induce quasi-isomorphisms on the underlying chain complexes $(\mathfrak{g},[-])$;

• fibrations include those morphisms that are degreewise surjections.

(Pridham 07), see this proposition.

Recall from def. that $\mathbf{B}^{p+1} \mathbb{R}$ denotes the line Lie (p+2)-algebra, whose Chevalley-Eilenberg algebra is generated in degree $(p+2)$ with vanishing differential.

then an $L_\infty$-algebra homomorphism

$$\mathfrak{g} \stackrel{\mu}{\longrightarrow} \mathbf{B}^{p+1}\mathbb{R}$$

Proposition

Given a (super-)Lie algebra $\mathfrak{g}$, then morphisms in $sL_\infty Alg$ of the form

$$\mu \colon \mathfrak{g} \longrightarrow \mathbf{B}^{p+1}\mathbb{R}$$

are in natural bijection with cocycles of degree $(p+2)$ in the standard Lie algebra cohomology of $\mathfrak{g}$.

Proof

Since the morphisms in $sL_\infty Alg$ are equivalent to morphisms going the other direction in $sdgAlg$ we have a bijection

$$\frac{g \longrightarrow \mathbf{B}^{p+1}\mathbb{R}}{CE(\mathfrak{g}) \longleftarrow (\langle c\rangle, d = 0)} \,.$$

Here the dg-algebra homomorphisms send the generator $c$ to some element $\mu$ of degree $(p+2)$ in $CE(\mathfrak{g})$, and the respect for the differential implies that $d_{CE(\mathfrak{g})} \mu = 0$. This is the classical definition of Lie algebra cocycles.

This immediately generalizes:

Definition

For $\mathfrak{g}$ a super-$L_\infty$ algebra, then an $\mathbb{R}$-valued $(p+2)$-cocycle on $\mathfrak{g}$ is a morphism in $sL_\infty Alg$ of the form

$$\mu \colon \mathfrak{g} \longrightarrow \mathbf{B}^{p+1}\mathbb{R}$$

hence equivalently an closed element $\mu \in CE(\mathfrak{g})$ of degree $(p+2)$.

The homotopy fiber of such $\mu$ is the L-∞ algebra extension $\hat \mathfrak{g}$ that it classifies

$$\array{ \hat \mathfrak{g} \\ \downarrow^{\mathrlap{hofib(\mu)}} \\ \mathfrak{g} &\stackrel{\mu}{\longrightarrow}& \mathbf{B}^{p+1}\mathbb{R} } \,.$$

Proposition

For $\mathfrak{g} \in sL\infty Alg$, the homotopy fiber $\hat {\mathfrak{g}}$ of a cocycle (def. ) $\mu \colon \mathfrak{g} \longrightarrow \mathbf{B}^{p+1} \mathbb{R}$ is given by

$$CE(\hat {\mathfrak{g}}) \simeq CE(\mathfrak{g})[b_{p+1}]/(d b_{p+1} = \mu) \,.$$

(Fiorenza-Rogers-Schreiber 13, theorem 3.1.13)

Example

For $\mathfrak{g}$ a Lie algebra and $\mu \in CE(\mathfrak{g})$ an ordinary 2-cocycle on $\mathfrak{g}$, then the homotopy fiber $\hat {\mathfrak{g}}$ of $\mu \colon \mathfrak{g}\longrightarrow \mathbf{B}\mathbb{R}$ is the classical central Lie algebra extension induced by $\mu$.

Example

For $\mathfrak{g}$ a semisimple Lie algebra and $\mathfrak{g} \stackrel{\langle-,[-,-]\rangle}{\longrightarrow} \mathbf{B}^2 \mathbb{R}$ the canonical 3-cocycle, its homotopy fiber is the string Lie 2-algebra.

These $L_\infty$-extension will in general carry new cocycles, so that towers and bouquets of higher extensions emanate from any one super $L_\infty$-algebra

$$\array{ \widehat{\hat \mathfrak{g}} \\ \downarrow^{\mathrlap{hofib(\mu_2)}} \\ \hat \mathfrak{g} &\stackrel{\mu_2}{\longrightarrow}& \mathbf{B}^{p_2 + 1} \mathbb{R} \\ \downarrow^{\mathrlap{hofib(\mu_1)}} \\ \mathfrak{g} &\stackrel{\mu_1}{\longrightarrow}& \mathbf{B}^{p_1+1}\mathbb{R} } \,.$$

This reminds one of Whitehead towers in homotopy theory. And indeed, there is Lie integration of $L_\infty$-algebras, which connects them both to smooth ∞-groups and to rational homotopy theory:

For $\mathfrak{g}$ a Lie algebra, then the 2-coskeleton of the simplicial set

$$\flat \exp(\mathfrak{g}) \;\colon\; [k] \mapsto Hom(CE(\mathfrak{g}), \Omega_{dR}^\bullet(\Delta^k))$$

is the simplicial nerve of the simply connected Lie group $G$ corresponding to $\mathfrak{g}$:

$$cosk_2 \flat \exp(\mathfrak{g}) \simeq N G \,.$$

To remember the smooth structure on $G$ we simply parameterize this over smooth manifolds $U$. Then the simplicial presheaf

$$\exp(\mathfrak{g}) \;\colon\; (U,[k]) \mapsto Hom(CE(\mathfrak{g}), \Omega_{vert}^\bullet(\U \times Delta^k))$$

gives the smooth stack delooping of the Lie group $G$:

$$cosk_2 \exp(\mathfrak{g}) \simeq \mathbf{B}G \,.$$

This generalizes verbatim to a Lie integration functor

$$\exp \;\colon\; sL_\infty Alg \longrightarrow PSh(SuperMfd, sSet)$$

from (super-)L-∞ algebras $\mathfrak{g}$ to simplicial presheaves over supermanifolds, hence (super-)smooth ∞-stacks.

(Henriques 08, Fiorenza-Schreiber-Stasheff 12).

Notice that for $CE(\mathfrak{g})$ a Sullivan model, then over the point this is the Sullivan construction of rational homotopy theory. For instance the Eilenberg-MacLane spaces

$$\flat \exp( \mathbf{B}^{p+1} \mathbb{R} ) \simeq K(\mathbb{R}, p+2)$$

This will be key in the following: $L_\infty$-theory allows to derive the cohomological nature of the charges of super p-branes, but only in rational homotopy theory. The open problem to be discussed below is concerned with the ambiguity of lifting this to genuine (non-rational) homotopy theory.

Homotopy theory

We will apply to the $L_\infty$-theoretic constructions above a higher analog of Lie integration, below, in order to pass from infinitesimal to finite structures. This requires some basics of homotopy theory and ∞-groupoid theory which we briefly review here. For more on the following see at geometry of physics – homotopy types and at geometry of physics – smooth homotopy types.

$\,$

One of the fundamental principles of modern physics is the gauge principle. It says that every field configuration in physics – hence absolutely everything in physics – is, in general, a gauge field configuration. This in turn means that given two field configurations $\Phi_1$ and $\Phi_2$, then it makes no sense to ask whether they are equal or not. Instead what makes sense to ask for is a gauge transformation $g$ that, if it exists, exhibits $\Phi_1$ as being gauge equivalent to $\Phi_2$ via $g$:

$$\Phi_1 \underoverset{\simeq}{g}{\longrightarrow} \Phi_2 \,.$$

This satisfies obvious rules, so obvious that physics textbooks usually don’t bother to mention this. First of all, if there is yet another field configuration $\Phi_3$ and a gauge transformation $g'$ from $\Phi_2$ to $\Phi_3$, then there is also the composite gauge transformation

$$g' \circ g \Phi_1 \underoverset{\simeq}{g}{\longrightarrow} \Phi_2 \underoverset{\simeq}{g'}{\longrightarrow} \Phi_3$$

and this composition is associative.

Moreover, these being equivalences means that they have inverses,

$$\Phi_2 \underoverset{\simeq}{g^{-1}}{\longrightarrow} \Phi_1$$

such that the compositions

$$\Phi_1 \underoverset{\simeq}{g}{\longrightarrow} \Phi_2 \underoverset{\simeq}{g^{-1}}{\longrightarrow} \Phi_1$$

and

$$\Phi_1 \underoverset{\simeq}{g}{\longrightarrow} \Phi_2 \underoverset{\simeq}{g^{-1}}{\longrightarrow} \Phi_1$$

equal the identity transformation.

Obvious as this may be, in mathematics such structure gets a name: this is a groupoid or homotopy 1-type whose objects are field configurations and whose morphisms are gauge transformations.

But notice that in the last statement above about inverses, we were actually violating the gauge principle: we asked for a gauge transformation of the form $g^{-1}\circ g$ (transforming one way and then just transforming back) to be equal to the identity transformation $id$.

But the gauge principle applies also to gauge transformations themselves. This is the content of higher gauge theory. For instance a 2-form gauge field such as the Kalb-Ramond field has gauge-of-gauge transformations. In the physics literature these are best known in their infinitesimal approximation, which are called ghost-of-ghost fields (for some historical reasons). In fact physicists know the infinitesimal “Lie algebroid” version of Lie groupoids and their higher versions as BRST complexes.

This means that in general it makes no sense to ask whether two gauge transformations are equal or not. What makes sense is to ask for a gauge-of-gauge transformation that turns one into the other

$$\array{ \Phi_1 & \stackrel{g}{\longrightarrow} & \Phi_2 \\ & \Downarrow^{\mathrlap{\simeq}} \\ \Phi_1 & \underset{g'}{\longrightarrow} & \Phi_2 } \,.$$

Now it is clear that gauge-of-gauge transformations may be composed with each other, and that, being equivalences, they have inverses under this composition. Moreover, this composition of gauge-of-gauge transformations is to be compatible with the already existing composition of the first order gauge transformations themselves. This structure, when made explicit, is in mathematics called a 2-groupoid or homotopy 2-type.

But now it is clear that this pattern continues: next we may have a yet higher gauge theory, for instance that of a 3-form C-field, and then there are third order gauge transformations which we must use to identify, when possible, second order gauge transformations. They may in turn be composed and have inverses under this composition, and the resulting structure, when made explicit, is called a 3-groupoid or homotopy 3-type.

This logic of the gauge principle keeps applying, and hence we obtain an infinite sequence of concepts, which at stage $n \in \mathbb{N}$ are called n-groupoids or homotopy n-types. The limiting case where we never assume that some high order gauge-of-gauge transformation has no yet higher order transformations between them, the structure in this limiting case accordingly goes by the name of infinity-groupoid or just homotopy type.

One way to make this idea of $\infty$-groupoids precise is to model them as Kan complexes. This we now explain.

$\,$

$$\array{ && && ([n] \mapsto \Delta^n) \\ \\ && && {topological \atop spaces} \\ && && \Bigg\downarrow{}^{\mathrlap{{higher \atop path}\atop groupoid}} & \\ ([n] \mapsto \Delta[n]) && groupoids &\stackrel{{Grothendieck \atop nerve}}{\longrightarrow}& { {\mathbf{Kan}\;\mathbf{complexes}} \atop {\simeq \infty-groupoids} } &\stackrel{{Dold-Kan \atop correspondence}}{\longleftarrow}& {chain \atop complexes} && ([n] \mapsto N(\Delta[n])) \\ && && \Bigg\downarrow{}^{\mathrlap{included \atop in}} \\ && && {simplicial \atop sets} }$$

We first review now “bare” homotopy types, meaning: homotopy types without any further geometric structure. Further below we equip bare homotopy types with smooth geometric structure and speak of smooth homotopy types.

This distinction between bare and smooth homotopy types is easily understood: bare homotopy types generalize discrete groups and groupoids (groupoids are homotopy 1-types), while smooth homotopy types generalize Lie groups and Lie groupoids (and diffeological groups and diffeological groupoids etc.).

bare homotopy types	smooth homotopy types
discrete groups, groupoids	Lie groups, Lie groupoids
2-groups, 2-groupoids	Lie 2-groups, Lie 2-groupoids
$\vdots$	$\vdots$
∞-groups,∞-groupoids	smooth ∞-groups, smooth ∞-groupoids

Remark

Beware that there is a deep fact which, when handled improperly, may mislead to suggest that there is geometry already in bare homotopy types. Namely each topological space represents a bare homotopy type and every bare homotopy type is represented by some topological space, up to equivalence (we come to this below). Due to this, it turns out that for instance every bare ∞-group is presented by a topological group. Nevertheless, however, the categories (in fact: (∞,1)-categories) of topological groups and of ∞-groups are not equivalent. Rather, the bare homotopy type represented by a topological space $X$ has the interpretation as being the fundamental ∞-groupoid of that topological space, a generalization of the more familiar fundamental groupoid. In passing from topological spaces to their fundamental ($\infty$-)groupoids the topological cohesion between their points is forgotten, and only the “shape” of the topological space is retained.

Bare homotopy types

Intuitive idea – Composition of higher order (gauge-)symmetries

An ∞-groupoid is, first of all, supposed to be a structure that has k-morphisms for all $k \in \mathbb{N}$, which for $k \geq 1$ go between $(k-1)$-morphisms. A useful tool for organizing such collections of morphisms is the notion of a simplicial set. This is a functor on the opposite category of the simplex category $\Delta$, whose objects are the abstract cellular $k$-simplices, denoted $[k]$ or $\Delta[k]$ for all $k \in \mathbb{N}$, and whose morphisms $\Delta[k_1] \to \Delta[k_2]$ are all ways of mapping these into each other. So we think of such a simplicial set given by a functor

$$K : \Delta^{op} \to Set$$

as specifying

• a set $[0] \mapsto K_0$ of objects;

• a set $[1] \mapsto K_1$ of morphisms;

• a set $[2] \mapsto K_2$ of 2-morphisms;

• a set $[3] \mapsto K_3$ of 3-morphisms;

and generally

• a set $[k] \mapsto K_k$ of k-morphisms

as well as specifying

• functions $([n] \hookrightarrow [n+1]) \mapsto (K_{n+1} \to K_n)$ that send $n+1$-morphisms to their boundary $n$-morphisms;

• functions $([n+1] \to [n]) \mapsto (K_{n} \to K_{n+1})$ that send $n$-morphisms to identity $(n+1)$-morphisms on them.

The fact that $K$ is supposed to be a functor enforces that these assignments of sets and functions satisfy conditions that make consistent our interpretation of them as sets of $k$-morphisms and source and target maps between these. These are called the simplicial identities.

But apart from this source-target matching, a generic simplicial set does not yet encode a notion of composition of these morphisms.

For instance for $\Lambda^1[2]$ the simplicial set consisting of two attached 1-cells

$$\Lambda^1[2] = \left\{ \array{ && 1 \\ & \nearrow && \searrow \\ 0 &&&& 2 } \right\}$$

and for $(f,g) : \Lambda^1[2] \to K$ an image of this situation in $K$, hence a pair $x_0 \stackrel{f}{\to} x_1 \stackrel{g}{\to} x_2$ of two composable 1-morphisms in $K$, we want to demand that there exists a third 1-morphisms in $K$ that may be thought of as the composition $x_0 \stackrel{h}{\to} x_2$ of $f$ and $g$. But since we are working in higher category theory, we want to identify this composite only up to a 2-morphism equivalence

$$\array{ && x_1 \\ & {}^{\mathllap{f}}\nearrow &\Downarrow^{\mathrlap{\simeq}}& \searrow^{\mathrlap{g}} \\ x_0 &&\stackrel{h}{\to}&& x_2 } \,.$$

From the picture it is clear that this is equivalent to demanding that for $\Lambda^1[2] \hookrightarrow \Delta[2]$ the obvious inclusion of the two abstract composable 1-morphisms into the 2-simplex we have a diagram of morphisms of simplicial sets

$$\array{ \Lambda^1[2] &\stackrel{(f,g)}{\to}& K \\ \downarrow & \nearrow_{\mathrlap{\exists h}} \\ \Delta[2] } \,.$$

A simplicial set where for all such $(f,g)$ a corresponding such $h$ exists may be thought of as a collection of higher morphisms that is equipped with a notion of composition of adjacent 1-morphisms.

For the purpose of describing groupoidal composition, we now want that this composition operation has all inverses. For that purpose, notice that for

$$\Lambda^2[2] = \left\{ \array{ && 1 \\ & && \searrow \\ 0 &&\to&& 2 } \right\}$$

the simplicial set consisting of two 1-morphisms that touch at their end, hence for

$$(g,h) : \Lambda^2[2] \to K$$

two such 1-morphisms in $K$, then if $g$ had an inverse $g^{-1}$ we could use the above composition operation to compose that with $h$ and thereby find a morphism $f$ connecting the sources of $h$ and $g$. This being the case is evidently equivalent to the existence of diagrams of morphisms of simplicial sets of the form

$$\array{ \Lambda^2[2] &\stackrel{(g,h)}{\to}& K \\ \downarrow & \nearrow_{\mathrlap{\exists f}} \\ \Delta[2] } \,.$$

Demanding that all such diagrams exist is therefore demanding that we have on 1-morphisms a composition operation with inverses in $K$.

In order for this to qualify as an $\infty$-groupoid, this composition operation needs to satisfy an associativity law up to coherent 2-morphisms, which means that we can find the relevant tetrahedras in $K$. These in turn need to be connected by pentagonators and ever so on. It is a nontrivial but true and powerful fact, that all these coherence conditions are captured by generalizing the above conditions to all dimensions in the evident way:

let $\Lambda^i[n] \hookrightarrow \Delta[n]$ be the simplicial set – called the $i$th $n$-horn – that consists of all cells of the $n$-simplex $\Delta[n]$ except the interior $n$-morphism and the $i$th $(n-1)$-morphism.

Then a simplicial set is called a Kan complex, if for all images $f : \Lambda^i[n] \to K$ of such horns in $K$, the missing two cells can be found in $K$- in that we can always find a horn filler $\sigma$ in the diagram

$$\array{ \Lambda^i[n] &\stackrel{f}{\to}& K \\ \downarrow & \nearrow_{\mathrlap{\sigma}} \\ \Delta[n] } \,.$$

The basic example is the nerve $N(C) \in sSet$ of an ordinary groupoid $C$, which is the simplicial set with $N(C)_k$ being the set of sequences of $k$ composable morphisms in $C$. The nerve operation is a full and faithful functor from 1-groupoids into Kan complexes and hence may be thought of as embedding 1-groupoids in the context of general ∞-groupoids.

Topological spaces as Kan complexes – Higher path groupoids

The concept of simplicial sets and of Kan complexes is secretly well familiar from the singular simplicial complex construction from the definition of singular homology and singular cohomology. In our context we may think of the singular simplicial complex of a topological space as being its fundamental infinity-groupoid of paths and higher paths. We here briefly review the standard definition and properties of the singular simplicial complex.

$\,$

Definition

For $n \in \mathbb{N}$, the topological n-simplex is, up to homeomorphism, the topological space whose underlying set is the subset

$$\Delta^n \coloneqq \{ \vec x \in \mathbb{R}^{n+1} | \sum_{i = 0 }^n x_i = 1 \; and \; \forall i . x_i \geq 0 \} \subset \mathbb{R}^{n+1}$$

of the Cartesian space $\mathbb{R}^{n+1}$, and whose topology is the subspace topology induces from the canonical topology in $\mathbb{R}^{n+1}$.

Remark

The coordinate expression in def. – also known as barycentric coordinates – is evidently just one of many possible ways to present topological $n$-simplices. Another common choice are what are called Cartesian coordinates. Of course nothing of relevance will depend on which choice of coordinate presentation is used, but some are more convenient in some situations than others.

Example

In low dimension the topological $n$-simplices of def. look as follows.

For $n = 0$ this is the point, $\Delta^0 = *$.

For $n = 1$ this is the standard interval object $\Delta^1 = [0,1]$.

For $n = 2$ this is the filled triangle.

For $n = 3$ this is the filled tetrahedron.

Definition

For $n \in \mathbb{N}$, $\n \geq 1$ and $0 \leq k \leq n$, the $k$th $(n-1)$-face (inclusion) of the topological $n$-simplex, def. , is the subspace inclusion

$$\delta_k : \Delta^{n-1} \hookrightarrow \Delta^n$$

induced under the coordinate presentation of def. , by the inclusion

$$\mathbb{R}^n \hookrightarrow \mathbb{R}^{n+1}$$

which “omits” the $k$th canonical coordinate:

$$(x_0, \cdots , x_{n-1}) \mapsto (x_0, \cdots, x_{k-1} , 0 , x_{k}, \cdots, x_{n-1}) \,.$$

Example

The inclusion

$$\delta_0 : \Delta^0 \to \Delta^1$$

is the inclusion

$$\{1\} \hookrightarrow [0,1]$$

of the “right” end of the standard interval. The other inclusion

$$\delta_1 : \Delta^0 \to \Delta^1$$

is that of the “left” end $\{0\} \hookrightarrow [0,1]$.

Definition

For $n \in \mathbb{N}$ and $0 \leq k \lt n$ the $k$th degenerate $(n)$-simplex (projection) is the surjective map

$$\sigma_k : \Delta^{n} \to \Delta^{n-1}$$

induced under the barycentric coordinates of def. under the surjection

$$\mathbb{R}^{n+1} \to \mathbb{R}^n$$

which sends

$$(x_0, \cdots, x_n) \mapsto (x_0, \cdots, x_{k} + x_{k+1}, \cdots, x_n) \,.$$

Definition

For $X \in$ Top a topological space and $n \in \mathbb{N}$ a natural number, a singular $n$-simplex in $X$ is a continuous map

$$\sigma : \Delta^n \to X$$

from the topological $n$-simplex, def. , to $X$.

Write

$$(Sing X)_n \coloneqq Hom_{Top}(\Delta^n , X)$$

for the set of singular $n$-simplices of $X$.

So to a topological space $X$ is associated a sequence of sets

$$(Sing X)_n \coloneqq Hom_{Top}(\Delta^n, X)$$

of singular simplices. Since the topological $n$-simplices $\Delta^n$ from def. sit inside each other by the face inclusions of def.

$$\delta_k : \Delta^{n-1} \to \Delta^{n}$$

and project onto each other by the degeneracy maps, def.

$$\sigma_k : \Delta^{n+1} \to \Delta^n$$

we dually have functions

$$d_k \coloneqq Hom_{Top}(\delta_k, X) : (Sing X)_n \to (Sing X)_{n-1}$$

that send each singular $n$-simplex to its $k$-face and functions

$$s_k \coloneqq Hom_{Top}(\sigma_k,X) : (Sing X)_{n} \to (Sing X)_{n+1}$$

that regard an $n$-simplex as beign a degenerate (“thin”) $(n+1)$-simplex. All these sets of simplicies and face and degeneracy maps between them form the following structure.

Definition

A simplicial set $S \in sSet$ is

• for each $n \in \mathbb{N}$ a set $S_n \in Set$ – the set of $n$-simplices;

• for each injective map $\delta_i : \overline{n-1} \to \overline{n}$ of totally ordered sets $\bar n \coloneqq \{ 0 \lt 1 \lt \cdots \lt n \}$

  a function $d_i : S_{n} \to S_{n-1}$ – the $i$th face map on $n$-simplices;

• for each surjective map $\sigma_i : \overline{n+1} \to \bar n$ of totally ordered sets

  a function $\sigma_i : S_{n} \to S_{n+1}$ – the $i$th degeneracy map on $n$-simplices;

such that these functions satisfy the simplicial identities.

Proposition

These face and degeneracy maps satisfy the following simplicial identities (whenever the maps are composable as indicated):

1. $d_i \circ d_j = d_{j-1} \circ d_i$ if $i \lt j$,

2. $s_i \circ s_j = s_j \circ s_{i-1}$ if $i \gt j$.

3. $d_i \circ s_j = \left\{ \array{ s_{j-1} \circ d_i & if \; i \lt j \\ id & if \; i = j \; or \; i = j+1 \\ s_j \circ d_{i-1} & if i \gt j+1 } \right.$

It is straightforward to check by explicit inspection that the evident injection and restriction maps between the sets of singular simplices make $(Sing X)_\bullet$ into a simplicial set. We now briefly indicate a systematic way to see this using basic category theory, but the reader already satisfied with this statement should skip ahead to the Singular chain complex.

Definition

The simplex category $\Delta$ is the full subcategory of Cat on the free categories of the form

$$\begin{aligned} [0] & \coloneqq \{0\} \\ [1] & \coloneqq \{0 \to 1\} \\ [2] & \coloneqq \{0 \to 1 \to 2\} \\ \vdots \end{aligned} \,.$$

Remark

This is called the “simplex category” because we are to think of the object $[n]$ as being the “spine” of the $n$-simplex. For instance for $n = 2$ we think of $0 \to 1 \to 2$ as the “spine” of the triangle. This becomes clear if we don’t just draw the morphisms that generate the category $[n]$, but draw also all their composites. For instance for $n = 2$ we have_

$$[2] = \left\{ \array{ && 1 \\ & \nearrow && \searrow \\ 0 &&\to&& 2 } \right\} \,.$$

Proposition

A functor

$$S : \Delta^{op} \to Set$$

from the opposite category of the simplex category to the category Set of sets is canonically identified with a simplicial set, def. .

Proof

One checks by inspection that the simplicial identities characterize precisely the behaviour of the morphisms in $\Delta^{op}([n],[n+1])$ and $\Delta^{op}([n],[n-1])$.

This makes the following evident:

Example

The topological simplices from def. arrange into a cosimplicial object in Top, namely a functor

$$\Delta^\bullet : \Delta \to Top \,.$$

With this now the structure of a simplicial set on $(Sing X)_\bullet$ is manifest: it is just the nerve of $X$ with respect to $\Delta^\bullet$, namely:

Definition

For $X$ a topological space its simplicial set of singular simplicies (often called the singular simplicial complex)

$$(Sing X)_\bullet : \Delta^{op} \to Set$$

is given by composition of the functor from example with the hom functor of Top:

$$(Sing X) : [n] \mapsto Hom_{Top}( \Delta^n , X ) \,.$$

The singular simplicial complex, def. , has a further special property which we discuss now.

Definition

For each $i$, $0 \leq i \leq n$, the $(n,i)$-horn or $(n,i)$-box is the subsimplicial set

$$\Lambda^i[n] \hookrightarrow \Delta[n]$$

which is the union of all faces except the $i^{th}$ one.

This is called an outer horn if $k = 0$ or $k = n$. Otherwise it is an inner horn.

Example

The inner horn, def. of the 2-simplex

$$\Delta^2 = \left\{ \array{ && 1 \\ & \nearrow &\Downarrow& \searrow \\ 0 &&\to&& 2 } \right\}$$

with boundary

$$\partial \Delta^2 = \left\{ \array{ && 1 \\ & \nearrow && \searrow \\ 0 &&\to&& 2 } \right\}$$

looks like

$$\Lambda^2_1 = \left\{ \array{ && 1 \\ & \nearrow && \searrow \\ 0 &&&& 2 } \right\} \,.$$

The two outer horns look like

$$\Lambda^2_0 = \left\{ \array{ && 1 \\ & \nearrow && \\ 0 &&\to&& 2 } \right\}$$

and

$$\Lambda^2_2 = \left\{ \array{ && 1 \\ & && \searrow \\ 0 &&\to&& 2 } \right\}$$

respectively.

Definition

A Kan complex is a simplicial set $S$ that satisfies the Kan condition,

• which says that all horns of the simplicial set have fillers/extend to simplices;

• which means equivalently that the unique homomorphism $S \to pt$ from $S$ to the point (the terminal simplicial set) is a Kan fibration;

• which means equivalently that for all diagrams in sSet of the form

  $$\array{ \Lambda^i[n] &\to& S \\ \downarrow && \downarrow \\ \Delta[n] &\to& pt } \;\;\; \leftrightarrow \;\;\; \array{ \Lambda^i[n] &\to& S \\ \downarrow && \\ \Delta[n] }$$

  there exists a diagonal morphism

  $$\array{ \Lambda^i[n] &\to& S \\ \downarrow &\nearrow& \downarrow \\ \Delta[n] &\to& pt } \;\;\; \leftrightarrow \;\;\; \array{ \Lambda^i[n] &\to& S \\ \downarrow &\nearrow& \\ \Delta[n] }$$

  completing this to a commuting diagram;

• which in turn means equivalently that the map from $n$-simplices to $(n,i)$-horns is an epimorphism

  $$[\Delta[n], S]\, \twoheadrightarrow \,[\Lambda^i[n],S] \,.$$

Proposition

The singular simplicial complex $Sing(X)$ , def. , of any topological space $X$ is a Kan complex, def. .

Proof

Write ${\vert \Lambda^i[n] \vert} \subset \mathbb{R}^{n+1}$ for the topological horn, the subspace of the topological $n$-simplex consisting of its boundary but excluding the interior of its $i$th face. From the geometry is clear that there exists a projection $\Delta^n \to {\vert \Lambda^i[n] \vert}$ which is a retract, in that the composite

$${\vert \Lambda^i[n]\vert} \hookrightarrow \Delta^n \to {\vert \Lambda^i[n]\vert}$$

is the identity. This provides the required fillers: if

$$\frac{ \Lambda^i[n] \longrightarrow Sing(X) } { {\vert \Lambda^i[n]\vert} \longrightarrow X }$$

is a given horn in the singular simplicial complex, then the composite

$$\Delta^n \to {\vert \Lambda^i[n]\vert} \longrightarrow X$$

is a filler.

Groupoids as Kan complexes – Grothendieck simplicial nerve

Definition

A (small) groupoid $\mathcal{G}_\bullet$ is

• a pair of sets $\mathcal{G}_0 \in Set$ (the set of objects) and $\mathcal{G}_1 \in Set$ (the set of morphisms)

• equipped with functions

  $$\array{ \mathcal{G}_1 \times_{\mathcal{G}_0} \mathcal{G}_1 &\stackrel{\circ}{\longrightarrow}& \mathcal{G}_1 & \stackrel{\overset{t}{\longrightarrow}}{\stackrel{\overset{i}{\leftarrow}}{\underset{s}{\longrightarrow}}}& \mathcal{G}_0 }\,,$$

  where the fiber product on the left is that over $\mathcal{G}_1 \stackrel{t}{\to} \mathcal{G}_0 \stackrel{s}{\leftarrow} \mathcal{G}_1$,

such that

• $i$ takes values in endomorphisms;

  $$t \circ i = s \circ i = id_{\mathcal{G}_0}, \;\;\;$$

• $\circ$ defines a partial composition operation which is associative and unital for $i(\mathcal{G}_0)$ the identities; in particular

  $s (g \circ f) = s(f)$ and $t (g \circ f) = t(g)$;

• every morphism has an inverse under this composition.

Remark

This data is visualized as follows. The set of morphisms is

$$\mathcal{G}_1 = \left\{ \phi_0 \stackrel{k}{\to} \phi_1 \right\}$$

and the set of pairs of composable morphisms is

$$\mathcal{G}_2 \coloneqq \mathcal{G}_1 \underset{\mathcal{G}_0}{\times} \mathcal{G}_1 = \left\{ \array{ && \phi_1 \\ & {}^{\mathllap{k_1}}\nearrow && \searrow^{\mathrlap{k_2}} \\ \phi_0 && \stackrel{k_2 \circ k_1}{\to} && \phi_2 } \right\} \,.$$

The functions $p_1, p_2, \circ \colon \mathcal{G}_2 \to \mathcal{G}_1$ are those which send, respectively, these triangular diagrams to the left morphism, or the right morphism, or the bottom morphism.

Example

For $X$ a set, it becomes a groupoid by taking $X$ to be the set of objects and adding only precisely the identity morphism from each object to itself

$$\left( X \stackrel {\overset{id}{\longrightarrow}} { \stackrel{\overset{id}{\longleftarrow}}{\underset{id}{\longrightarrow}} } X \right) \,.$$

Example

For $G$ a group, its delooping groupoid $(\mathbf{B}G)_\bullet$ has

• $(\mathbf{B}G)_0 = \ast$;

• $(\mathbf{B}G)_1 = G$.

For $G$ and $K$ two groups, group homomorphisms $f \colon G \to K$ are in natural bijection with groupoid homomorphisms

$$(\mathbf{B}f)_\bullet \;\colon\; (\mathbf{B}G)_\bullet \to (\mathbf{B}K)_\bullet \,.$$

In particular a group character $c \colon G \to U(1)$ is equivalently a groupoid homomorphism

$$(\mathbf{B}c)_\bullet \;\colon\; (\mathbf{B}G)_\bullet \to (\mathbf{B}U(1))_\bullet \,.$$

Here, for the time being, all groups are discrete groups. Since the circle group $U(1)$ also has a standard structure of a Lie group, and since later for the discussion of Chern-Simons type theories this will be relevant, we will write from now on

$$\flat U(1) \in Grp$$

to mean explicitly the discrete group underlying the circle group. (Here “$\flat$” denotes the “flat modality”.)

Example

For $X$ a set, $G$ a discrete group and $\rho \colon X \times G \to X$ an action of $G$ on $X$ (a permutation representation), the action groupoid or homotopy quotient of $X$ by $G$ is the groupoid

$$X//_\rho G = \left( X \times G \stackrel{\overset{\rho}{\longrightarrow}}{\underset{p_1}{\longrightarrow}} X \right)$$

with composition induced by the product in $G$. Hence this is the groupoid whose objects are the elements of $X$, and where morphisms are of the form

$$x_1 \stackrel{g}{\to} x_2 = \rho(x_1)(g)$$

for $x_1, x_2 \in X$, $g \in G$.

As an important special case we have:

Example

For $G$ a discrete group and $\rho$ the trivial action of $G$ on the point $\ast$ (the singleton set), the corresponding action groupoid according to def. is the delooping groupoid of $G$ according to def. :

$$(\ast //G)_\bullet = (\mathbf{B}G)_\bullet \,.$$

Another canonical action is the action of $G$ on itself by right multiplication. The corresponding action groupoid we write

$$(\mathbf{E}G)_\bullet \coloneqq G//G \,.$$

The constant map $G \to \ast$ induces a canonical morphism

$$\array{ G//G & \simeq & \mathbf{E}G \\ \downarrow && \downarrow \\ \ast //G & \simeq & \mathbf{B}G } \,.$$

This is known as the $G$-universal principal bundle. See below in for more on this.

Definition

For $\mathcal{G}_\bullet$ a groupoid, def. , its simplicial nerve $N(\mathcal{G}_\bullet)_\bullet$ is the simplicial set with

$$N(\mathcal{G}_\bullet)_n \coloneqq \mathcal{G}_1^{\times_{\mathcal{G}_0}^n}$$

the set of sequences of composable morphisms of length $n$, for $n \in \mathbb{N}$;

with face maps

$$d_k \colon N(\mathcal{G}_\bullet)_{n+1} \to N(\mathcal{G}_\bullet)_{n}$$

being,

• for $n = 0$ the functions that remembers the $k$th object;

• for $n \geq 1$

  • the two outer face maps $d_0$ and $d_n$ are given by forgetting the first and the last morphism in such a sequence, respectively;

  • the $n-1$ inner face maps $d_{0 \lt k \lt n}$ are given by composing the $k$th morphism with the $k+1$st in the sequence.

The degeneracy maps

$$s_k \colon N(\mathcal{G}_\bullet)n \to N(\mathcal{G}_\bullet)_{n+1} \,.$$

are given by inserting an identity morphism on $x_k$.

Remark

Spelling this out in more detail: write

$$\mathcal{G}_n = \left\{ x_0 \stackrel{f_{0,1}}{\to} x_1 \stackrel{f_{1,2}}{\to} x_2 \stackrel{f_{2,3}}{\to} \cdots \stackrel{f_{n-1,n}}{\to} x_n \right\}$$

for the set of sequences of $n$ composable morphisms. Given any element of this set and $0 \lt k \lt n$, write

$$f_{i-1,i+1} \coloneqq f_{i,i+1} \circ f_{i-1,i}$$

for the comosition of the two morphism that share the $i$th vertex.

With this, face map $d_k$ acts simply by “removing the index $k$”:

$$d_0 \colon (x_0 \stackrel{f_{0,1}}{\to} x_1 \stackrel{f_{1,2}}{\to} x_{2} \cdots \stackrel{f_{n-1,n}}{\to} x_n ) \mapsto (x_1 \stackrel{f_{1,2}}{\to} x_{2} \cdots \stackrel{f_{n-1,n}}{\to} x_n )$$

$$d_{0\lt k \lt n} \colon ( x_0 \cdots \stackrel{}{\to} x_{k-1} \stackrel{f_{k-1,k}}{\to} x_k \stackrel{f_{k,k+1}}{\to} x_{k+1} \stackrel{}{\to} \cdots x_n ) \mapsto ( x_0 \cdots \stackrel{}{\to} x_{k-1} \stackrel{f_{k-1,k+1}}{\to} x_{k+1} \stackrel{}{\to} \cdots x_n )$$

$$d_n \colon ( x_0 \stackrel{f_{0,1}}{\to} \cdots \stackrel{f_{n-2,n-1}}{\to} x_{n-1} \stackrel{f_{n-1,n}}{\to} x_n ) \mapsto ( x_0 \stackrel{f_{0,1}}{\to} \cdots \stackrel{f_{n-2,n-1}}{\to} x_{n-1} ) \,.$$

Similarly, writing

$$f_{k,k} \coloneqq id_{x_k}$$

for the identity morphism on the object $x_k$, then the degenarcy map acts by “repeating the $k$th index”

$$s_k \colon ( x_0 \stackrel{}{\to} \cdots \to x_k \stackrel{f_{k,k+1}}{\to} x_{k+1} \to \cdots ) \mapsto ( x_0 \stackrel{}{\to} \cdots \to x_k \stackrel{f_{k,k}}{\to} x_k \stackrel{f_{k,k+1}}{\to} x_{k+1} \to \cdots ) \,.$$

This makes it manifest that these functions organise into a simplicial set.

Proposition

These collections of maps in def. satisfy the simplicial identities, hence make the nerve $\mathcal{G}_\bullet$ into a simplicial set. Moreover, this simplicial set is a Kan complex, where each horn has a unique filler (extension to a simplex).

(A 2-coskeletal Kan complex.)

Proposition

The nerve operation constitutes a full and faithful functor

$$N \colon Grpd \to KanCplx \hookrightarrow sSet \,.$$

Chain complexes as Kan complexes – Dold-Kan-Moore correspondence

In the familiar construction of singular homology recalled above one constructs the alternating face map chain complex of the simplicial abelian group of singular simplices, def. . This construction is natural and straightforward, but the result chain complex tends to be very “large” even if its chain homology groups end up being very “small”. But in the context of homotopy theory one is to consider all objects notup to isomorphism, but of to weak equivalence, which for chain complexes means up to quasi-isomorphisms. Hence one should look for the natural construction of “smaller” chain complexes that are still quasi-isomorphic to these alternating face map complexes. This is accomplished by the normalized chain complex construction:

Definition

For $A$ a simplicial abelian group its alternating face map complex $(C A)_\bullet$ of $A$ is the chain complex which

• in degree $n$ is given by the group $A_n$ itself

  $$(C A)_n := A_n$$

• with differential given by the alternating sum of face maps (using the abelian group structure on $A$)

  $$\partial_n \coloneqq \sum_{i = 0}^n (-1)^i d_i \;\colon\; (C A)_n \to (C A)_{n-1} \,.$$

Lemma

The differential in def. is well-defined in that it indeed squares to 0.

Proof

Using the simplicial identity, prop. , $d_i \circ d_j = d_{j-1} \circ d_i$ for $i \lt j$ one finds:

$$\begin{aligned} \partial_n \partial_{n+1} & = \sum_{i, j} (-1)^{i+j} d_i \circ d_{j} \\ &= \sum_{i \geq j} (-1)^{i+j} d_i \circ d_j + \sum_{i \lt j} (-1)^{i+j} d_i \circ d_j \\ &= \sum_{i \geq j} (-1)^{i+j} d_i \circ d_j + \sum_{i \lt j} (-1)^{i+j} d_{j-1} \circ d_i \\ &= \sum_{i \geq j} (-1)^{i+j} d_i \circ d_j - \sum_{i \leq k} (-1)^{i+k} d_{k} \circ d_i \\ &= 0 \end{aligned} \,.$$

Definition

Given a simplicial abelian group $A$, its normalized chain complex or Moore complex is the $\mathbb{N}$-graded chain complex $((N A)_\bullet,\partial )$ which

• is in degree $n$ the joint kernel

  $$(N A)_n=\bigcap_{i=1}^{n}ker\,d_i^n$$

  of all face maps except the 0-face;

• with differential given by the remaining 0-face map

  $$\partial_n := d_0^n|_{(N A)_n} : (N A)_n \rightarrow (N A)_{n-1} \,.$$

Remark

We may think of the elements of the complex $N A$, def. , in degree $k$ as being $k$-dimensional disks in $A$ all whose boundary is captured by a single face:

• an element $g \in N G_1$ in degree 1 is a 1-disk

  $$1 \stackrel{g}{\to} \partial g \,,$$

• an element $h \in N G_2$ is a 2-disk

  $$\array{ && 1 \\ & {}^1\nearrow &\Downarrow^h& \searrow^{\partial h} \\ 1 &&\stackrel{1}{\to}&& 1 } \,,$$

• a degree 2 element in the kernel of the boundary map is such a 2-disk that is closed to a 2-sphere

  $$\array{ && 1 \\ & {}^1\nearrow &\Downarrow^h& \searrow^{\partial h = 1} \\ 1 &&\stackrel{1}{\to}&& 1 } \,,$$

etc.

Definition

Given a simplicial group $A$ (or in fact any simplicial set), then an element $a \in A_{n+1}$ is called degenerate (or thin) if it is in the image of one of the simplicial degeneracy maps $s_i \colon A_n \to A_{n+1}$. All elements of $A_0$ are regarded a non-degenerate. Write

$$D (A_{n+1}) \coloneqq \langle \cup_i s_i(A_{n}) \rangle \hookrightarrow A_{n+1}$$

for the subgroup of $A_{n+1}$ which is generated by the degenerate elements (i.e. the smallest subgroup containing all the degenerate elements).

Definition

For $A$ a simplicial abelian group its alternating face maps chain complex modulo degeneracies, $(C A)/(D A)$ is the chain complex

• which in degree 0 equals is just $((C A)/D(A))_0 \coloneqq A_0$;

• which in degree $n+1$ is the quotient group obtained by dividing out the group of degenerate elements, def. :

  $$((C A)/D(A))_{n+1} := A_{n+1} / D(A_{n+1})$$

• whose differential is the induced action of the alternating sum of faces on the quotient (which is well-defined by lemma ).

Lemma

Def. is indeed well defined in that the alternating face map differential respects the degenerate subcomplex.

Proof

Using the mixed simplicial identities we find that for $s_j(a) \in A_n$ a degenerate element, its boundary is

$$\begin{aligned} \sum_i (-1)^i d_i s_j(a) &= \sum_{i \lt j} (-1)^i s_{j-1} d_i(a) + \sum_{i = j, j+1} (-1)^i a + \sum_{i \gt j+1} (-1)^i s_j d_{i-1}(a) \\ &= \sum_{i \lt j} (-1)^i s_{j-1} d_i(a) + \sum_{i \gt j+1} (-1)^i s_j d_{i-1}(a) \end{aligned}$$

which is again a combination of elements in the image of the degeneracy maps.

Proposition

Given a simplicial abelian group $A$, the evident composite of natural morphisms

$$N A \stackrel{i}{\hookrightarrow} A \stackrel{p}{\to} (C A)/(D A)$$

from the normalized chain complex, def. , into the alternating face map complex modulo degeneracies, def. , (inclusion followed by projection to the quotient) is a natural isomorphism of chain complexes.

Corollary

For $A$ a simplicial abelian group, there is a splitting

$$C_\bullet(A) \simeq N_\bullet(A) \oplus D_\bullet(A)$$

of the alternating face map complex, def. as a direct sum, where the first direct summand is naturally isomorphic to the normalized chain complex of def. and the second is the degenerate cells from def. .

Proof

By prop. there is an inverse to the diagonal composite in

$$\array{ C A &\stackrel{p}{\longrightarrow}& (C A)/(D A) \\ {}^{\mathllap{i}}\uparrow & \nearrow \\ N A } \,.$$

This hence exhibits a splitting of the short exact sequence given by the quotient by $D A$.

$$\array{ 0 &\to& D A &\hookrightarrow & C A &\stackrel{p}{\longrightarrow}& (C A)/(D A) &\to & 0 \\ && && {}^{\mathllap{i}}\uparrow & \swarrow_{\mathrlap{\simeq}_{iso}} \\ && && N A } \,.$$

Theorem (Eilenberg-MacLane)

Given a simplicial abelian group $A$, then the inclusion

$$N A \hookrightarrow C A$$

of the normalized chain complex, def. into the full alternating face map complex, def. , is a natural quasi-isomorphism and in fact a natural chain homotopy equivalence, i.e. the complex $D_\bullet(X)$ is null-homotopic.

Corollary

Given a simplicial abelian group $A$, then the projection chain map

$$(C A) \longrightarrow (C A)/(D A)$$

from its alternating face maps complex, def. , to the alternating face map complex modulo degeneracies, def. , is a quasi-isomorphism.

Proof

Consider the pre-composition of the map with the inclusion of the normalized chain complex, def. .

$$\array{ C A &\stackrel{p}{\longrightarrow}& (C A)/(D A) \\ {}^{\mathllap{i}}\uparrow & \nearrow \\ N A }$$

By theorem the vertical map is a quasi-isomorphism and by prop. the composite diagonal map is an isomorphism, hence in particular also a quasi-isomorphism. Since quasi-isomorphisms satisfy the two-out-of-three property, it follows that also the map in question is a quasi-isomorphism.

Example

Consider the 1-simplex $\Delta[1]$ regarded as a simplicial set, and write $\mathbb{Z}[\Delta[1]]$ for the simplicial abelian group which in each degree is the free abelian group on the simplices in $\Delta[1]$.

This simplicial abelian group starts out as

$$\mathbb{Z}[\Delta[1]] = \left( \cdots \stackrel{\longrightarrow}{\stackrel{\longrightarrow}{\stackrel{\longrightarrow}{\longrightarrow}}} \mathbb{Z}^4 \stackrel{\longrightarrow}{\stackrel{\longrightarrow}{\longrightarrow}} \mathbb{Z}^3 \stackrel{\overset{\partial_0}{\longrightarrow}}{\underset{\partial_1}{\longrightarrow}} \mathbb{Z}^2 \right)$$

(where we are indicating only the face maps for notational simplicity).

Here the first $\mathbb{Z}^2 = \mathbb{Z}\oplus \mathbb{Z}$, the direct sum of two copies of the integers, is the group of 0-chains generated from the two endpoints $(0)$ and $(1)$ of $\Delta[1]$, i.e. the abelian group of formal linear combinations of the form

$$\mathbb{Z}^2 \simeq \left\{ a \cdot (0) + b \cdot (1) | a,b \in \mathbb{Z}\right\} \,.$$

The second $\mathbb{Z}^3 \simeq \mathbb{Z}\oplus \mathbb{Z}\oplus \mathbb{Z}$ is the abelian group generated from the three (!) 1-simplicies in $\Delta[1]$, namely the non-degenerate edge $(0\to 1)$ and the two degenerate cells $(0 \to 0)$ and $(1 \to 1)$, hence the abelian group of formal linear combinations of the form

$$\mathbb{Z}^3 \simeq \left\{ a \cdot (0\to 0) + b \cdot (0 \to 1) + c \cdot (1 \to 1) | a,b,c \in \mathbb{Z}\right\} \,.$$

The two face maps act on the basis 1-cells as

$$\partial_1 \colon (i \to j) \mapsto (i)$$

$$\partial_0 \colon (i \to j) \mapsto (j) \,.$$

Now of course most of the (infinitely!) many simplices inside $\Delta[1]$ are degenerate. In fact the only non-degenerate simplices are the two 0-cells $(0)$ and $(1)$ and the 1-cell $(0 \to 1)$. Hence the alternating face maps complex modulo degeneracies, def. , of $\mathbb{Z}[\Delta[1]]$ is simply this:

$$(C (\mathbb{Z}[\Delta[1]])) / D (\mathbb{Z}[\Delta[1]])) = \left( \cdots \to 0 \to 0 \to \mathbb{Z} \stackrel{\left(1 \atop -1\right)}{\longrightarrow} \mathbb{Z}^2 \right) \,.$$

Notice that alternatively we could consider the topological 1-simplex $\Delta^1 = [0,1]$ and its singular simplicial complex $Sing(\Delta^1)$ in place of the smaller $\Delta[1]$, then the free simplicial abelian group $\mathbb{Z}(Sing(\Delta^1))$ of that. The corresponding alternating face map chain complex $C(\mathbb{Z}(Sing(\Delta^1)))$ is “huge” in that in each positive degree it has a free abelian group on uncountably many generators. Quotienting out the degenerate cells still leaves uncountably many generators in each positive degree (while every singular $n$-simplex in $[0,1]$ is “thin”, only those whose parameterization is as induced by a degeneracy map are actually regarded as degenerate cells here). Hence even after normalization the singular simplicial chain complex is “huge”. Nevertheless it is quasi-isomorphic to the tiny chain complex found above.

The statement of the Dold-Kan correspondence now is the following.

Theorem

For $A$ an abelian category there is an equivalence of categories

$$N \;\colon\; A^{\Delta^{op}} \stackrel{\leftarrow}{\to} Ch_\bullet^+(A) \;\colon\; \Gamma$$

between

• the category of simplicial objects in $A$;

• the category of connective chain complexes in $A$;

where

• $N$ is the normalized chains complex/normalized Moore complex functor.

Theorem (Kan)

For the case that $A$ is the category Ab of abelian groups, the functors $N$ and $\Gamma$ are nerve and realization with respect to the cosimplicial chain complex

$$\mathbb{Z}[-]: \Delta \to Ch_+(Ab)$$

that sends the standard $n$-simplex to the normalized Moore complex of the free simplicial abelian group $F_{\mathbb{Z}}(\Delta^n)$ on the simplicial set $\Delta^n$, i.e.

$$\Gamma(V) \;\colon\; [k] \mapsto Hom_{Ch_\bullet^+(Ab)}(N(\mathbb{Z}(\Delta[k])), V) \,.$$

Example

Given a chain complex $V$, consider the 1-simplices of its incarnation $\Gamma(V)$ as a simplicial set. By theorem these correspond to the maps of chain complexes

$$N( \mathbb{Z}[\Delta[1]] ) \longrightarrow V$$

from the normalized chains complex of the 1-simplex. By example the latter is

$$\left( \cdots \to 0 \to 0 \to \mathbb{Z} \stackrel{\left(1 \atop -1\right)}{\longrightarrow} \mathbb{Z}^2 \right) \,.$$

Hence a map of chain complexes as above is:

1. two group homomorphisms $\alpha,\beta \colon \mathbb{Z}\longrightarrow V_0$, hence equivalently two elements $\alpha,\beta \in V_0$;

2. one group homomorphism $\kappa \colon \mathbb{Z} \longrightarrow V_1$, hence equivalently an element $\kappa \in V_1$;

3. such that

   $$\array{ \mathbb{Z} &\stackrel{\kappa}{\longrightarrow}& V_1 \\ \downarrow^{\mathrlap{(1,-1)}} && \downarrow^{\mathrlap{\partial_V}} \\ \mathbb{Z} \oplus \mathbb{Z} &\stackrel{(\beta,\alpha)}{\longrightarrow}& V_0 }$$

   i.e. such that

   $\partial_V \kappa = \beta - \alpha$.

Generally we have the following

Proposition

• For $V \in Ch_\bullet^+$ the simplicial abelian group $\Gamma(V)$ is in degree $n$ given by

  $$\Gamma(V)_n = \bigoplus_{[n] \underset{surj}{\to} [k]} V_k$$

  and for $\theta : [m] \to [n]$ a morphism in $\Delta$ the corresponding map $\Gamma(V)_n \to \Gamma(V)_m$

  $$\theta^* : \bigoplus_{[n] \underset{surj}{\to} [k]} V_k \to \bigoplus_{[m] \underset{surj}{\to} [r]} V_r$$

  is given on the summand indexed by some $\sigma : [n] \to [k]$ by the composite

  $$V_k \stackrel{d^*}{\to} V_s \hookrightarrow \bigoplus_{[m] \underset{surj}{\to} [r]} V_r$$

  where

  $$[m] \stackrel{t}{\to} [s] \stackrel{d}{\to} [k]$$

  is the epi-mono factorization of the composite $[m] \stackrel{\theta}{\to} [n] \stackrel{\sigma}{\to} [k]$.

• The natural isomorphism $\Gamma N \to Id$ is given on $A \in sAb^{\Delta^{op}}$ by the map

  $$\bigoplus_{[n] \underset{surj}{\to} [k]} (N A)_k \to A_n$$

  which on the direct summand indexed by $\sigma : [n] \to [k]$ is the composite

  $$N A_k \hookrightarrow A_k \stackrel{\sigma^*}{\to} A_n \,.$$

• The natural isomorphism $Id \to N \Gamma$ is on a chain complex $V$ given by the composite of the projection

  $$V \to C(\Gamma(V)) \to C(\Gamma(C))/D(\Gamma(V))$$

  with the inverse

  $$C(\Gamma(V))/D(\Gamma(V)) \to N \Gamma(V)$$

  of

  $$N \Gamma(V) \hookrightarrow C(\Gamma(V)) \to C(\Gamma(V))/D(\Gamma(V))$$

  (which is indeed an isomorphism, as discussed at Moore complex).

Proposition

With the explicit choice for $\Gamma N \stackrel{\simeq}{\to} Id$ as above we have that $\Gamma$ and $N$ form an adjoint equivalence $(\Gamma \dashv N)$

Remark

It follows that with the inverse structure maps, we also have an adjunction the other way round: $(N \dashv \Gamma)$.

Hence in concclusion the Dold-Kan correspondence allows us to regard chain complexes (in non-negative degree) as, in particular, special simplicial sets. In fact as simplicial sets they are Kan complexes and hence infinity-groupoids:

Theorem (J. C. Moore)

The simplicial set underlying any simplicial group (by forgetting the group structure) is a Kan complex.

In fact, not only are the horn fillers guaranteed to exist, but there is an algorithm that provides explicit fillers. This implies that constructions on a simplicial group that use fillers of horns can often be adjusted to be functorial by using the algorithmically defined fillers. An argument that just uses ‘existence’ of fillers can be refined to give something more ‘coherent’.

Smooth homotopy types

For detailed lecture notes see at geometry of physics – smooth sets and geometry of physics – smooth homotopy types.

$\,$

Where a simplicial set or Kan complex is a model for a bare homotopy type, in order to equip such with smooth structure we may just add the information that says for each Cartesian space $\mathbb{R}^n$ what the collection of smooth maps into our smooth-homotopy-type-to-be-described is. That collection should itslef be a Kan complex (exhibiting the fact that between any two smooth maps there may be equivalences, and higher order equivalences).

This means that we consider smooth homotopy types to be given by simplicial presheaves

$$X \;\colon\; CartSp^{op} \longrightarrow sSet \,.$$

Example

By the Grothendieck nerve construction discussed above, every Lie groupoid $\mathcal{G}$ induces a simplicial presheaf, the one which to a test Cartesian space $U$ assigns the nerve of the bare groupoid of smooth functions into $\mathcal{G}$:

$$\mathcal{G} \;\colon\; U \mapsto N\left( \array{ C^\infty(U, \mathcal{G}_1) \\ \downarrow \uparrow \downarrow \\ C^\infty(U, \mathcal{G}_0) } \right) \,.$$

In particular for $G$ a Lie group with $\mathbf{B}G$ the corresponding one-object Lie groupoid, then its incarnation as a simplicial sheaf is

$$\mathbf{B}G \;\colon\; U \mapsto N\left( \array{ C^\infty(U, G) \\ \downarrow \uparrow \downarrow \\ \ast } \right) \,.$$

Example

By the Dold-Kan correspondence discussed above, every presheaf of chain complexes on CartSp presents a simplicial presheaf. In particular every bare chain complex gives a constant simplicial presheaf. Let $A$ be a discrete abelian group and write $A[n]$ for the chain complex concentrated on $A$ in degree $n$, then we write

$$\mathbf{B}^n A \coloneqq \Gamma(A[n]) \in KanCplx \stackrel{constant}{\longrightarrow} PSh(CartSp,sSet)$$

for the corresponding simplicial presheaf.

On the other hand, let $C^\infty(-)\colon CartSp^{op} \longrightarrow Ab$ be the sheaf of smooth functions, regarded as taking values in additive abelian groups. Then we write

$$\mathbf{B}^n \mathbb{R} \coloneqq \Gamma(C^\infty(-)[n]) \in PSh(CartSp, sSet) \,.$$

In contrast, the simplicial presheaf which comes from the real numbers regarded as a discrete group we write

$$\mathbf{B}^n \flat \mathbb{R}\coloneqq \Gamma(\mathbb{R}[n]) \stackrel{const}{\longrightarrow} PSh(CartSp, sSet) \,.$$

In order to get the right homotopy theory of such smooth homotopy types, we just need to declare that a morphism between two such simplicial presheaves is a weak equivalence if it restricts to a weak homotopy equivalence between simplicial sets/Kan complexes on small enough neighbourhoods (i.e. stalks) around any point.

We write

$$L_{lwhe} PSh(CartSp,Set)$$

for the resulting homotopy theory of simplicial presheaves with weak equivalences the stalk-wise weak homotopy equivalences. Technically this is the (∞,1)-topos which arises from simplicial localization of the simplicial presheaves at the local weak homotopy equivalences. In practice, the main point to know about this is that it means that for $X$ and $A$ two presheaves with values in Kan complexes, then a homomorphism between them in $L_{lwhe} PSh(CartSp,Set)$ is in general a span of plain morphisms in $L_{lwhe} PSh(CartSp,Set)$,

$$\array{ \hat X &\longrightarrow& Y \\ \downarrow^{\mathrlap{\simeq_{l}}} \\ X }$$

where the left morphism, is a stalkwise weak homotopy equivalence. This just means that when mapping between the simplicial presheaves, we need to remember that we may replace the domain by locally weakly equivalent object.

This procedure of exhibiting morphisms in a homotopy they by spans in a more naive theory is more widely known in the context of Lie groupoids, where such spans are known as Morita morphisms or Hilsum-Skandalis morphisms or groupoid bibundles or what not. These are the special case of the above spans when $X$ and $Y$ happen to be (the simplicial presheaves represented by) Lie groupoids. More technical discussion of what is really going on here is at category of fibrant objects.

Example

For $X$ a smooth manifold and $G$ a Lie group, they represent simplicial sheaves $X$ and $\mathbf{B}G$ via example . A morphism from $X$ to $\mathbf{B}G$ in the homotopy theory of smooth homotopy types may pass through an locally weakly equivalent resolution of $X$. Such is given by any choice of open cover $\{U_i \to X\}$. Let $C(\{U_i\})$ be the corresponding Cech nerve, then a span as above is given by

$$\array{ C(\{U_i\}) &\longrightarrow& \mathbf{B}G \\ \downarrow^{\mathrlap{\simeq_w}} \\ X } \,.$$

Inspection shows that here the top morphism is equivalently a Cech cocycle on $X$ with coefficients in $G$, representing a $G$-principal bundle on $X$.

For more lecture notes on this see at geometry of physics – principal bundles.

Example

We write

$$\mathbf{B}^{p+1}(\mathbb{R}/\Gamma)_{conn} \;\colon\; U \mapsto \Gamma\left( \Gamma \hookrightarrow C^\infty(U,\mathbb{R}) \stackrel{d_{dR}}{\longrightarrow} \Omega^1(U) \stackrel{d_{dR}}{\longrightarrow} \Omega^2(U) \stackrel{d_{dR}}{\longrightarrow} \cdots \stackrel{d_{dR}}{\longrightarrow} \Omega^n(U) \right)$$

for the incarnation of the Deligne complex (in the given degrees) as a simplicial presgeaf, via the Dold-Kan correspondence.

Then for $X$ a smooth manifold as in example , a morphism from $X$ to \mathbf[B}^{p+1}(\mathbb{R}/\Gamma)_{conn} in the homotopy theory of simplicial presheaves is equivalently a choice $\mathbf[B}\{U_i \to X\}$ of a good open cover and a span

$$\array{ C(\{U_i\}) &\longrightarrow& \mathbf{B}^{p+1}(\mathbb{R}/\Gamma)_{conn} \\ \downarrow^{\mathrlap{\simeq_w}} \\ X } \,.$$

Inspection shows that these are equivalently the Cech-Deligne cocyles discussed above.

Higher Lie integration

We discuss differential refinements of the “path method” of Lie integration for L-infinity-algebras. The key observation for interpreting the following def. is this:

Remark

For $\mathfrak{g}$ an L-∞ algebra, and given a smooth manifold $U$, then

1. the flat L-∞ algebra valued differential forms on $U$ are equivalently the dg-algebra homomorphisms

   $$\Omega_{flat}(U,\mathfrak{g}) = Hom_{dgAlg}(CE(\mathfrak{g}), \Omega^\bullet(U)_{\mathrm{dR}})$$

2. a finite gauge transformation between two such forms is equivalently a homotopy

   $$\array{ & & \Omega_{flat}(U \times \Delta^1,\mathfrak{g}) \\ & {}^{(-)|_0}\swarrow && \searrow^{\mathrlap{(-)|_1}} \\ \Omega_{flat}(U ,\mathfrak{g}) && && \Omega_{flat}(U, \mathfrak{g}) } \,.$$

For more details see at infinity-Lie algebroid-valued differential form – Integration of infinitesimal gauge transformations.

Definition

For $\mathfrak{g}$ an L-∞ algebra, write:

• $CE(\mathfrak{g})$ for the Chevalley-Eilenberg algebra of an L-∞ algebra $\mathfrak{g}$;

• $\Delta^\bullet_{smth} \colon \Delta \to SmoothMfd$ for the cosimplicial smooth manifold with corners which is in degree $k$ the standard $k$-simplex $\Delta^k \hookrightarrow \mathbb{R}^{k+1}$;

• $\Omega^\bullet_{si}(\Delta_{smth}^k)$ for the de Rham complex of those differential forms on $\Delta_{smth}^k$ which have sitting instants, in that in an open neighbourhood of the boundary they are constant perpendicular to any face on their value at that face;

• $\Omega^\bullet_{si}(U \times \Delta_{smth}^k)$ for $U \in SmoothMfd$ for the de Rham complex of differential forms on $U \times \Delta^k$ which when restricted to each point of $U$ have sitting instants on $\Delta^k$;

• $\Omega^\bullet_{vert,si}(U \times \Delta_{smth}^k)$ for the subcomplex of forms that in addition are vertical differential forms with respect to the projection $U \times \Delta^k \to U$.

Definition

For $\mathfrak{g}$ an L-∞ algebra, write

• $\exp(\mathfrak{g})_\bullet \in PreSmoothTypes = PSh(CartSp,sSet)$

  for the simplicial presheaf

  $$\exp(\mathfrak{g}) \colon (U \times k) \mapsto Hom_{dgAlg}( CE(\mathfrak{g}), \Omega^\bullet_{vert,si}(U \times \Delta_{smth}^k) ) \,.$$

  which is the universal Lie integration of $\mathfrak{g}$;

• $\flat_{dR}\exp(\mathfrak{g})_\bullet \in PreSmoothTypes = PSh(CartSp,sSet)$

  for the simplicial presheaf

  $$\flat_{dR}\exp(\mathfrak{g})_\bullet \;\colon\; (U \times k) \mapsto Hom_{dgAlg}( CE(\mathfrak{g}), \Omega^{\bullet\geq 1, \bullet}_{si}(U \times \Delta^k_{smth}) )$$

  of those differential forms on $U \times \Delta^\bullet$ with at least one leg along $U$;

• $\Omega^1_{flat}(-,\mathfrak{g}) \coloneqq \flat_{dR}\exp(\mathfrak{g})_0 \longrightarrow \flat_{dR}\exp(\mathfrak{g})_\bullet$

  for the canonical inclusion of the degree-0 piece, regarded as a simplicial constant simplicial presheaf.

Example

From the discussion at Lie integration:

1. $\Omega^1_{flat}(-,b^{p+1}\mathbb{R}) = \mathbf{\Omega}^{p+2}_{cl}$;

2. for $\mathfrak{g}$ an ordinary Lie algebra, then for the 2-coskeleton (by this discussion)

   $$cosk_2 \exp(\mathfrak{g}) \simeq \mathbf{B}G_\bullet$$

   for $G$ the simply connected Lie group associated to $\mathfrak{g}$ by traditional Lie theory. If $\mathfrak{g}$ is furthermore a semisimple Lie algebra, then also

   $$cosk_3 \exp(\mathfrak{g}) \simeq \mathbf{B}G_\bullet$$

3. for $\mathfrak{g} = b^{p}\mathbb{R}$ the line Lie p+1-algebra, then (by this proposition)

   $$\exp(b^p \mathbb{R}) \simeq \mathbf{B}^{p+1}\mathbb{R} \,.$$

Remark

The constructions in def. are clearly functorial: given a homomorphism of L-∞ algebras

$$\mu \;\colon\; \mathfrak{g} \longrightarrow \mathfrak{h}$$

it prolongs to a homomorphism of presheaves

$$\mu \colon \Omega^1_{flat}(-,\mathfrak{g}) \longrightarrow \Omega^1(-,\mathfrak{h})$$

and of simplicial presheaves

$$\exp(\mu) \;\colon\; \exp(\mathfrak{g}) \longrightarrow \exp(\mathfrak{h})$$

etc.

Example

According to the above, a degree-$(p+2)$-L-∞ cocycle $\mu$ on an L-∞ algebra $\mathfrak{g}$ is a homomorphism of the form

$$\mu \colon \mathfrak{g} \longrightarrow b^{p+1}\mathbb{R}$$

to the line Lie (p+2)-algebra $b^{p+1}\mathbb{R}$. The formal dual of this is the homomorphism of dg-algebras

$$CE(\mathfrak{g}) \longleftarrow CE(b^{p+1}\mathbb{R}) \colon \mu^\ast$$

which manifestly picks a $d_{CE(\mathfrak{g})}$-closed element in $CE^{p+2}(\mathfrak{g})$.

Precomposing this $\mu^\ast$ with a flat L-∞ algebra valued differential form

$$A \in \Omega^1_{flat}(X,\mathfrak{g}) = Hom_{dgAlg}(CE(\mathfrak{g}), \Omega^\bullet(X))$$

yields, by example , a plain closed $(p+2)$-form

$$\mu^\ast A \in \Omega^{p+2}_{cl}(X) \,.$$

Definition

Given an L-∞ cocycle

$$\mu \colon \mathfrak{g} \longrightarrow b^{p+1}\mathbb{R} \,,$$

as in example , then its group of periods is the discrete additive subgroup $\Gamma \hookrightarrow \mathbb{R}$ of those real numbers which are integrations

$$\underset{\partial \Delta^{p+3}_{smth}}{\int} \mu^\ast A \in \mathbb{R}$$

of the value of $\mu$, as in example , on L-∞ algebra valued differential forms

$$A \in \Omega^1_{flat}(\partial \Delta^{p+3}_{smth}) \,,$$

over the boundary of the (p+3)-simplex (which are forms with sitting instants on the $(p+2)$-dimensional faces that glue together; without restriction of generality we may simply consider forms on the $(p+2)$-sphere $S^{p+2}$).

Proposition

Given an L-∞ cocycle $\mu \colon \mathfrak{g} \to b^{p+1}\mathbb{R}$, as in example , then the universal Lie integration of $\mu$, via def. and remark , descends to the $(p+2)$-coskeleton

$$\mathbf{B}G \coloneqq cosk_{p+2}\exp(\mathfrak{g})$$

up to quotienting the coefficients $\mathbb{R}$ by the group of periods $\Gamma$ of $\mu$, def. , to yield the bottom morphism in

$$\array{ \exp(\mathfrak{g}) &\stackrel{\exp(\mu)}{\longrightarrow}& \mathbf{B}^{p+2}\mathbb{R} \\ \downarrow && \downarrow \\ \mathbf{B}G &\stackrel{\mathbf{c}}{\longrightarrow}& \mathbf{B}^{p+2} (\mathbb{R}/\Gamma) } \,.$$

This is due to (FSS 12).

Here and in the following we are freely using example to identify $\exp(b^{p+1}\mathbb{R}) \simeq \mathbf{B}^{p+2}\mathbb{R}$. Establishing this is the only real work in prop. .

Higher Maurer-Cartan forms

Definition

Write

$$\flat \;\colon\; L_{lwhe} PSh(\mathrm{CartSp}, sSet) \longrightarrow L_{lwhe} PSh(\mathrm{CartSp}, sSet)$$

for the operation that evaluates a simplicial presheaf on the point and then extends the result back as a constant presheaf. This comes with a canonical counit natural transformation

$$\epsilon^\flat \colon \flat \to Id \,.$$

Example

For $G$ a Lie group and

$$\mathbf{B}G : U \mapsto N C^\infty(U,G) \in L_{lwhe} PSh(\mathrm{CartSp}, sSet)$$

for its stacky delooping, which is the universal moduli stack of $G$-principal bundles, then given a $G$-principal bundle $P$ modulated by a map

$$X \longrightarrow \mathbf{B}G$$

then a lift $\nabla$ in the homotopy-commutative diagram

$$\array{ && \flat \mathbf{B}G \\ &{}^{\mathllap{\nabla}}\nearrow& \downarrow \\ X &\longrightarrow& \mathbf{B}G }$$

is equivalently a flat connection on $G$. Hence $\flat \mathbf{B}G$ is the universal moduli stack for flat connections. Whence the symbol “$\flat$”.

Definition

Given $G$ any smooth infinity-group, denote the double homotopy fiber of the counit $\epsilon^\flat$, def. as follows:

$$\array{ G \\ \downarrow^{\mathrlap{G}} \\ \flat_{dR} \mathbf{B}G &\longrightarrow& \flat \mathbf{B}G \\ && \downarrow^{\mathrlap{\epsilon^{\flat}}} \\ && \mathbf{B}G } \,.$$

We say that

• $\flat_{dR}\mathbf{B}G$ is the flat de Rham coefficients for $G$;

• $\theta_G$ is the Maurer-Cartan form of $G$.

Example

In the situation of example where $G$ is an ordinary Lie groups and with $\mathfrak{g}$ denoting the Lie algebra of $G$, then we get that

• $\flat_{dR}\mathbf{B}G \simeq \Omega^1_{flat}(-,\mathfrak{g})$ is the sheaf of flat Lie algebra valued differential forms;

• $\theta_{G}$ is (under the Yoneda embedding) the Maurer-Cartan form on $G$ in the traditional sense.

Higher WZW terms

We discuss now how every L-∞ cocycle $\mu \;\colon\; \mathfrak{g} \longrightarrow b^{p+1} \mathbb{R}$ induces via differential higher Lie integration a higher WZW term for a $p$-brane sigma model with target space a differential extension $\tilde G$ of a smooth infinity-group $G$ that integrates $\mathfrak{g}$. In the next section below we characterize these differential extensions and find that they are given by bundles of moduli stacks for higher gauge fields on the $p$-brane worldvolume. This means that the higher WZW terms obtained here are in fact higher analogs of the gauged WZW model.

(The following construction is from FSS 13, section 5, streamlined a little.)

$\,$

Proposition

For $\mu \colon \mathfrak{g}\longrightarrow b^{p+1}\mathbb{R}$ an L-∞ cocycle, then there is the following canonical commuting diagram of simplicial presheaves

$$\array{ \Omega^1_{flat}(-,G) &\stackrel{\mu}{\longrightarrow}& \Omega^2_{cl}(-,\mathbb{G}) \\ \downarrow && \downarrow \\ \flat_{dR}\mathbf{B}G &\stackrel{\flat_{dR} \mathbf{c}}{\longrightarrow}& \flat_{dR}\mathbf{B}^2 \mathbb{G} } \;\;\; \coloneqq \;\;\; \array{ \Omega^1_{flat}(-,\mathfrak{g}) &\stackrel{\mu}{\longrightarrow}& \mathbf{\Omega}^{p+2}_{cl} \\ \downarrow && \downarrow \\ \flat_{dR}\exp(\mathfrak{g})_\bullet & \stackrel{\flat_{dR}\exp(\mu)}{\longrightarrow} & \flat_{dR}\mathbf{B}^{p+2}\mathbb{R} \\ \downarrow && \downarrow \\ \flat_{dR}\mathbf{B}G &\stackrel{\flat_{dR}\mathbf{c}}{\longrightarrow}& \flat_{dR}\mathbf{B}^{p+2}\mathbb{R} }$$

which is given

• on the top by def. , example , remark ,

• on the bottom by applying the operation of def. to the commuting diagram provided by prop. ,

Notice that the abstractly define Maurer-Cartan form $\theta_G \;\colon\; G \longrightarrow \flat_{dR}\mathbf{B}G$ is, for $G$ a general smooth infinity-group, generically modeled not by a globally defined ordinary differential form, but by a Cech cocycle with coefficients in a simplicial complex of differential forms. The following definition is usefully thought of as constructing the universal cover $\widetilde G \longrightarrow G$ such that pulled back to this $\widetilde G$ the abstractly defined Maurer-Cartan form does become equivalent to a globally defined flat $\mathfrak{g}$-valued differential form. This in turn may be thought of as one of the defining properties of higher WZW terms: that their curvature is a globally defined and left invariant flat $\mathfrak{g}$-valued differential form.

Definition

Write

$$\tilde G \coloneqq G \underset{\flat_{dR}\mathbf{B}G}{\times} \mathbf{\Omega}^1_{flat}(-,\mathfrak{g})$$

for the homotopy pullback of the left vertical morphism in prop. along (the modulating morphism for) the Maurer-Cartan form $\theta_G$ of $G$, i.e. for the object sitting in a homotopy Cartesian square of the form

$$\array{ \tilde G &\stackrel{\theta_{\tilde G}}{\longrightarrow}& \Omega^1_{flat}(-,\mathfrak{g}) \\ \downarrow && \downarrow \\ G &\stackrel{\theta_G}{\longrightarrow}& \flat_{dR}\mathbf{B}G } \,.$$

Example

For the special case that $G$ is an ordinary Lie group, then $\flat_{dR}\mathbf{B}G \simeq \Omega^{1}_{flat}(-,\mathfrak{g})$, by example , hence in this case the morphism being pulled back in def. is an equivalence, and so in this case nothing new happens, we get $\tilde G \simeq G$.

On the other extreme, when $G = \mathbf{B}^{p}U(1)$ is the circle (p+1)-group, then def. reduces to the homotopy pullback that characterizes the Deligne complex and hence yields

$$\widetilde{\mathbf{B}^p U(1)} \simeq \mathbf{B}^p U(1)_{conn} \,.$$

This shows that def. is a certain non-abelian generalization of ordinary differential cohomology. We find further characterization of this below in corollary , see remark .

Remark

From example one reads off the conceptual meaning of def. : For $G$ a Lie group, then the de Rham coefficients are just globally defined differential forms, $\flat_{dR}\mathbf{B}G \simeq \Omega^1_{flat}(-,\mathfrak{g})$ (by the discussion here), and in particular therefore the Maurer-Cartan form $\theta_G \colon G \to \flat_{dR}\mathbf{B}G$ is a globally defined differential form. This is no longer the case for general smooth ∞-groups $G$. In general, the Maurer-Cartan forms here is a cocycle in hypercohomology, given only locally by differential forms, that are glued nontrivially, in general, via gauge transformations and higher gauge transformations given by lower degree forms.

But the WZW terms that we are after are supposed to prequantizations of globally defined Maurer-Cartan forms. The homotopy pullback in def. is precisely the universal construction that enforces the existence of a globally defined Maurer-Cartan form for $G$, namely $\theta_{\tilde G} \colon \tilde G \to \Omega^1_{flat}(-,\mathfrak{g})$.

Definition

Given an L-∞ cocycle $\mu \colon \mathfrak{g}\longrightarrow b^{p+1}\mathbb{R}$, then via prop. , prop. and using the naturality of the Maurer-Cartan form, def. , we have a morphism of cospan diagrams of the form

$$\array{ \Omega^1_{flat}(-,\mathfrak{g}) &\stackrel{\mu}{\longrightarrow}& \mathbf{\Omega}^{p+2}_{cl} \\ \downarrow && \downarrow \\ \flat_{dR} \mathbf{B}G &\stackrel{\flat_{dR}\mathbf{c}}{\longrightarrow}& \flat_{dR}\mathbf{B}^{p+2}\mathbb{R} \\ \uparrow^{\mathrlap{\theta_G}} && \uparrow^{\mathrlap{\theta_{\mathbf{B}^{p+1}(\mathbb{R}/\Gamma)}}} \\ G &\stackrel{\Omega \mathbf{c}}{\longrightarrow}& \mathbf{B}^{p+1} (\mathbb{R}/\Gamma) } \,.$$

By the homotopy fiber product characterization of the Deligne complex, prop. , this yields a morphism of the form

$$\mathbf{L}_{WZW}^{\mu} \;\colon\; \tilde G \longrightarrow \mathbf{B}^{p+1}(\mathbb{R}/\Gamma)_{conn} \,.$$

which modulates a p+1-connection/Deligne cocycle on the differentially extended smooth $\infty$-group $\tilde G$ from def. .

This we call the WZW term obtained by universal Lie integration from $\mu$.

Essentially this construction originates in (FSS 13).

Remark

The WZW term of def. is a prequantization of $\omega \coloneqq \mu(\theta_{\tilde G})$, hence a lift $\mathbf{L}_{WZW}^\mu$ in

$$\array{ && \mathbf{B}^{p+1}(\mathbb{R}/\Gamma)_{conn} \\ & {}^{\mathllap{\mathbf{L}_{WZW}^\mu}}\nearrow & \downarrow^{\mathrlap{F_{(-)}}} \\ \tilde G &\stackrel{\mu(\theta_{\tilde G})}{\longrightarrow}& \mathbf{\Omega}^{p+2} } \,.$$

Consecutive WZW terms and twists

Above we discussed how a single L-∞ cocycle Lie integrates to a higher WZW term. More generally, one has a sequence of L-∞ cocycles, each defined on the extension that is classified by the previous one – a bouquet of cocycles. Here we discuss how in this case the higher WZW terms at each stage relate to each other. (The following statements are corollaries of FSS 13, section 5).

$\,$

In each stage, for $\mu_1 \colon \mathfrak{g}\to b^{p_1+1}\mathbb{R}$ a cocycle and $\hat {\mathfrak{g}} \to \mathfrak{g}$ the extension that it classifies (its homotopy fiber), then the next cocycle is of the form $\mu_2 \colon \hat \mathfrak{g} \to b^{p_2+1}\mathbb{R}$

$$\array{ \hat {\mathfrak{g}} &\stackrel{\mu_2}{\longrightarrow}& b^{p_2+1}\mathbb{R} \\ \downarrow \\ \mathfrak{g} &\stackrel{\mu_1}{\longrightarrow}& b^{p_1+1}\mathbb{R} } \,.$$

Lemma

The homotopy fiber $\hat \mathfrak{g} \to \mathfrak{g}$ of $\mu_1$ is given by the ordinary pullback

$$\array{ \hat \mathfrak{g} &\longrightarrow& e b^{p_1} \mathbb{R} \\ \downarrow && \downarrow \\ \mathfrak{g} &\stackrel{\mu_1}{\longrightarrow}& b^{p_1+1}\mathbb{R} } \,,$$

where $e b^{p_1}\mathbb{R}$ is defined by its Chevalley-Eilenberg algebra $CE(e b^{p_1}\mathbb{R})$ being the Weil algebra of $b^{p_1}\mathbb{R}$, which is the free differential graded algebra on a generator in degree $p_1$, and where the right vertical map takes that generator to 0 and takes its free image under the differential to the generator of $CE(b^{p_1+1}\mathbb{R})$.

Proof

This follows with the recognition principle for L-∞ homotopy fibers.

Corollary

A homotopy fiber sequence of L-∞ algebras $\hat \mathfrak{g} \to \mathfrak{g}\stackrel{\mu}{\longrightarrow} b^{p+1}\mathbb{R}$ induces a homotopy pullback diagram of the associated objects of L-∞ algebra valued differential forms, def. , of the form

$$\array{ \mathbf{\Omega}^1_{flat}(-,\hat {\mathfrak{g}}) &\stackrel{}{\longrightarrow}& \mathbf{\Omega}^{p+1} \\ \downarrow && \downarrow^{\mathbf{d}} \\ \mathbf{\Omega}^1_{flat}(-,\mathfrak{g}) &\stackrel{\mu}{\longrightarrow}& \mathbf{\Omega}^{p+2}_{cl} }$$

(hence an ordinary pullback of presheaves, since these are all simplicially constant).

Proof

The construction $\mathfrak{g} \mapsto Hom_{dgAlg}(CE(\mathfrak{g}), \Omega^\bullet(-))$ preserves pullbacks ($CE$ is an anti-equivalence onto its image, pullbacks of (pre-)-sheaves are computed objectwise, the hom-functor preserves pullbacks in the covariant argument).

Observe then (see the discussion at L-∞ algebra valued differential forms), that while

$$\mathbf{\Omega}^{p+2}_{cl} \simeq Hom_{dgAlg}(CE(b^{p+1}), \Omega^\bullet(-))$$

we have

$$\mathbf{\Omega}^{p+1} \simeq Hom_{dgAlg}(W(b^{p}), \Omega^\bullet(-)) \,.$$

With this the statement follows by lemma .

Definition

We say that a pair of L-∞ cocycles $(\mu_1, \mu_2)$ is consecutive if the domain of the second is the extension (homotopy fiber) defined by the first

$$\array{ \hat {\mathfrak{g}} &\stackrel{\mu_2}{\longrightarrow}& b^{p_2+1} \\ \downarrow \\ \mathfrak{g} &\stackrel{\mu_1}{\longrightarrow}& b^{p_1+1}\mathbb{R} }$$

and if the truncated Lie integrations of these cocycles via prop. preserves the extension property in that also

$$\hat G \longrightarrow G \overset{\Omega \mathbf{c}_1}{\longrightarrow} \mathbf{B}^{p_1+1}(\mathbb{R}/\Gamma_1)$$

is a homotopy fiber sequence of smooth homotopy types.

Remark

The issue of the second clause in def. is to do with the truncation degrees: the universal untruncated Lie integration $\exp(-)$ preserves homotopy fiber sequences, but if there are non-trivial cocycles on $\mathfrak{g}$ in between $\mu_1$ and $\mu_2$, for $p_2 \gt p_1$, then these will remain as nontrivial homotopy groups in the higher-degree truncation $\mathbf{B}G_{2} \coloneqq \tau_{p_2}\exp(\hat\mathfrak{g})$ (see Henriques 06, theorem 6.4) but they will be truncated away in $\mathbf{B}G_1 \coloneqq \tau_{p_1}\exp(\mathfrak{g})$ and will hence spoil the preservation of the homotopy fibers through Lie integration.

Notice that extending along consecutive cocycles is like the extension stages in a Whitehead tower.

Given two consecutive L-∞ cocycles $(\mu_1,\mu_2)$, def. , let

$$\mathbf{L}_1 \colon \tilde G \longrightarrow \mathbf{B}^{p_1+1}(\mathbb{R}/\Gamma_1)_{conn}$$

and

$$\mathbf{L}_2 \colon \widetilde {\hat G} \longrightarrow \mathbf{B}^{p_2+1}(\mathbb{R}/\Gamma_2)_{conn}$$

be the WZW terms obtained from the two cocycles via def. .

Proposition

There is a homotopy pullback square in smooth homotopy types of the form

$$\array{ \widetilde {\hat G} &\stackrel{}{\longrightarrow}& \mathbf{\Omega}^{p_1+1} \\ \downarrow && \downarrow \\ \tilde G &\stackrel{\mathbf{L}_1}{\longrightarrow}& \mathbf{B}^{p_1+1}(\mathbb{R}/\Gamma_1)_{conn} } \,.$$

Proof

Consider the following pasting composite

$$\array{ \mathbf{\Omega}^{p_1+1} &\longrightarrow& \ast &\longleftarrow& \ast \\ {}^{\mathllap{\mathbf{d}}}\downarrow &\swArrow& \downarrow && \downarrow \\ \mathbf{\Omega}^{p_1+2} &\longrightarrow& \flat_{dR}\mathbf{B}^{p_1+2}\mathbb{R} &\stackrel{\theta_{\mathbf{B}^{p_1}\mathbb{R}}}{\longleftarrow}& \mathbf{B}^{p_1+1}\mathbb{R} \\ \uparrow^{\mathrlap{\mu_1}} && \uparrow^{\mathrlap{\flat_{dR} \mathbf{c}_1 }} && \uparrow^{\mathrlap{\Omega \mathbf{c}_1}} \\ \mathbf{\Omega}^1_{flat}(-,\mathfrak{g}) &\stackrel{}{\longrightarrow}& \flat_{dR}\mathbf{B}G &\stackrel{\theta_G}{\longleftarrow}& G } \,,$$

where

• the top left square is the evident homotopy;

• the bottom left square is from prop. ;

• the top right square expresses that $\theta$ preserves the basepoint;

• the bottom right square is the naturality of the Maurer-Cartan form construction.

Under forming homotopy limits over the horizontal cospan diagrams here, this turns into

$$\array{ \mathbf{\Omega}^{p_1+1} \\ \downarrow \\ \mathbf{B}^{p_1+1}(\mathbb{R}/\Gamma_1)_{conn} \\ \uparrow^{\mathrlap{\mathbf{L}_1}} \\ \tilde G }$$

by def. . On the other hand, forming homotopy limits vertically this turns into

$$\array{ \mathbf{\Omega}^1_{flat}(-,\hat \mathfrak{g}) &\longrightarrow& \flat_{dR}\mathbf{B}G_2 &\stackrel{\theta_{\hat G}}{\longleftarrow}& \hat G }$$

(on the left by corollary , on the right by the second clause in def. ).

The homotopy limit over that last cospan, in turn, is $\widetilde{\hat G}$. This implies the claim by the fact that homotopy limits commute with each other.

Remark

Prop. says how consecutive pairs of $L_\infty$-cocycles Lie integrate suitably to consecutive pairs of WZW terms.

Corollary

In the above situation there is a homotopy fiber sequence of infinity-group objects of the form

$$\array{ \mathbf{B}^{p_1}(\mathbb{R}/\Gamma_1)_{conn} &\longrightarrow& \widetilde {\hat G} \\ && \downarrow \\ && \tilde G &\overset{\mathbf{L}_1}{\longrightarrow}& \mathbf{B}\left( \mathbf{B}^{p_1}(\mathbb{R}/\Gamma_1)_{conn} \right) } \,,$$

where the bottom horizontal morphism is the higher WZW term that Lie integrates $\mu_1$, followed by the canonical projection

$$\mathbf{B}^{p_1+1}(\mathbb{R}/\Gamma_1)_{conn} \to \mathbf{B}\left( \mathbf{B}^{p_1}(\mathbb{R}/\Gamma_1)_{conn} \right)$$

which removes the top-degree differential form data from a higher connection.

Hence $\widetilde{\hat G}$ is an infinity-group extension of $\tilde G$ by the moduli stack of higher connections.

Proof

By prop. and the pasting law, the homotopy fiber of $\widetilde {\hat G} \to \tilde G$ is equivalently the homotopy fiber of $\mathbf{\Omega}^{p_1+1}\to \mathbf{B}^{p_1+1}(\mathbb{R}/\Gamma_1)_{conn}$, which in turn is equivalently the homotopy fiber of $\ast \to \mathbf{B}\left( \mathbf{B}^{p_1}(\mathbb{R}/\Gamma_1)_{conn} \right)$, which is $\mathbf{B}\left( \mathbf{B}^{p_1}(\mathbb{R}/\Gamma_1)_{conn} \right)$:

$$\array{ \mathbf{B}^{p_1}(\mathbb{R}/\Gamma_1)_{conn} &\longrightarrow& \widetilde {\hat G} &\overset{}{\longrightarrow}& \mathbf{\Omega}^{p_1+1} &\overset{}{\longrightarrow}& \ast \\ \downarrow &(pb)& \downarrow &(pb)& \downarrow &(pb)& \downarrow \\ \ast &\longrightarrow& \tilde G &\stackrel{\mathbf{L}_1}{\longrightarrow}& \mathbf{B}^{p_1+1}(\mathbb{R}/\Gamma_1)_{conn} &\overset{}{\longrightarrow}& \mathbf{B}\left( \mathbf{B}^{p_1}(\mathbb{R}/\Gamma_1)_{conn} \right) } \,.$$

Remark

Corollary says that $\widetilde {\hat G}$ is a bundle of moduli stacks for differential cohomology over $\tilde G$. This means that maps

$$\Sigma \longrightarrow \widetilde{\hat G}$$

(which are the fields of the higher WZW model with WZW term $\mathbf{L}_2$) are pairs of plain maps $\phi \colon \Sigma \to \tilde G$ together with a differential cocycle on $\Sigma$, i.e. a $p_1$-form connection on $\Sigma$, which is twisted by $\phi$ in a certain way.

Below we discuss that this occurs for the (properly globalized) Green-Schwarz super p-brane sigma models of all the D-branes and of the M5-brane. For the D-branes $p_1 = 1$ and so there is a 1-form connection on their worldvolume, the Chan-Paton gauge field. For the M5-brane $p_1 = 2$ and so there is a 2-form connection on its worldvolume, the self-dual higher gauge field in 6d.

Example

For each Dp-brane species in type IIA string theory there is a pair of consecutive cocycles (def. ) of the form

$$\array{ \mathfrak{string}_{IIA} &\overset{\mu_{Dp}}{\longrightarrow}& b^{p+1} \mathbb{R} \\ \downarrow \\ \mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}} &\overset{\mu_{F1}^{IIA}}{\longrightarrow}& b^2 \mathbb{R} } \,.$$

This is by the discussion below. Here

$$\mu_{Dp} = (C \wedge \exp(F_2))_{p+2}$$

reflects the familiar D-brane coupling to the RR-fields $C = C_2 + C_4 + \cdots$, given an abelian Chan-Paton gauge field with field strength $F_2$, see def. below.

The WZW term induced by $\mu_{F1}^{IIA}$ is the globalization of the original term introduced by Green and Schwarz in the construction of the Green-Schwarz sigma-model for the superstring.

Now corollary says in this case that the Dp-brane sigma model has as target space the smooth super 2-group $\widetilde{ String_{IIA} }$ which is an infinity-group extension of super Minkowski spacetime by the moduli stack $\mathbf{B}U(1)_{conn}$ for complex line bundles with connection, sitting in a homotopy fiber sequence of the form

$$\array{ \mathbf{B}U(1)_{conn} &\longrightarrow& \widetilde{ String_{IIA} } \\ && \downarrow \\ && \mathbb{R}^{9,1\vert \mathbf{16}+ \overline{\mathbf{16}}} &\overset{\mathbf{L}_{Dp}}{\longrightarrow}& \mathbf{B}(\mathbf{B}^{p}U(1)_{conn}) } \,.$$

It follows that field configurations for the D-brane given by morphisms

$$\Sigma_{p+1} \longrightarrow \widetilde{ String_{IIA} }$$

are equivalently pairs, consisting of an ordinary sigma-model field

$$\phi \;\colon\; \Sigma_{p+1} \longrightarrow \mathbb{R}^{9,1\vert \mathbf{16}+ \overline{\mathbf{16}}}$$

together with a twisted 1-form connection on $\Sigma$, the twist depending on $\phi$. (In fact here the twist vanishes in bosonic degrees, unless we introduce a nontrivial bosonic component of the B-field). This is just the right datum of the (abelian) Chan-Paton gauge field on the D-brane.

Consecutive WZW terms descending to twisted cocycles

Above we considered consecutive cocycles (def. ) with coefficients in line Lie-n algebras $b^{p+1}\mathbb{R}$. Here we discuss how these may descend to single cocycles with richer coefficients.

Below we find as examples of this general phenomenon

1. the descent of the separate D-brane cocycles to the RR-fields in twisted K-theory, rationally (here)

2. the descent of the M5-brane cocycle to a cocycle in degree-4 cohomology, rationally (here).

$\,$

Given one stage of consecutive $L_\infty$-cocycles, def. (e.g in the brane bouquet discussed below)

$$\array{ \hat \mathfrak{g} & \stackrel{\mu_2}{\longrightarrow} & \mathbf{B}\mathfrak{h}_2 \\ {}^{\mathllap{hofib(\mu_1)}}\downarrow \\ \mathfrak{g} \\ & {}_{\mathllap{\mu_1}}\searrow \\ && \mathbf{B}\mathfrak{h}_1 }$$

then $\hat \mathfrak{g}$ may be thought of, in a precise sense, as being a $\mathfrak{h}_1$-principal ∞-bundle over $\mathfrak{g}$.

This and the following statements all are the general theorems of (Nikolaus-Schreiber-Stevenson 12) specified to $L_\infty$-algebras regarded as infinitesimal $\infty$-stacks (aka “formal moduli problems”) according to dcct. Here we do not not have the space to dwell further on the details of this general theory of higher principal bundles, but the reader familiar with Lie groupoids gets an accurate impression by considering the analogous situation in that context (see at geometry of physics – principal bundles for detailed lecture notes that cover the following):

for $H$ a Lie group and $\mathbf{B}H$ its one-object delooping Lie groupoid, and for $G$ another Lie group (or just any smooth manifold), then a generalized morphism of Lie groupoids

$$\array{ G \\ & \searrow \\ && \mathbf{B}H }$$

(i.e. a morphism between the smooth stacks which they represent, or equivalently a bibundle of Lie groupoids) classifies a smooth $H$-principal bundle over $H$, and the total space $\hat G$ of that bundle is equivalently the homotopy fiber of the original map.

$$\array{ \hat G \\ \downarrow \\ G \\ & \searrow \\ && \mathbf{B}H }$$

This is explained in some detail at principal bundle – In a (2,1)-topos.

Back to the abalogous situation of $L_\infty$-algebras instead of Lie groups, it is now natural to ask whether the second cocycle $\mu_2$, defined on the total space (stack) of this bundle is equivariant under the ∞-action of $\mathfrak{h}_1$. If $\mu_2$ does not itself already come from the base space, then it can at best be equivariant with respect to an $\mathfrak{h}_1$-∞-action on $\mathbf{B}\mathfrak{h}_2$.

A first observation now is that specifying such ∞-action $\rho$ is equivalent to specifying a second homotopy fiber sequence of the form as on the right of this completed diagram:

$$\array{ \hat \mathfrak{g} && \stackrel{\mu_2}{\longrightarrow} && \mathbf{B}\mathfrak{h}_2 \\ {}^{\mathllap{hofib(\mu_1)}}\downarrow && && \downarrow^{\mathrlap{hofib(p_\rho)}} \\ \mathfrak{g} && && (\mathbf{B}\mathfrak{h}_2)/\mathfrak{h}_1 \\ & {}_{\mathllap{\mu_1}}\searrow && \swarrow_{\mathrlap{p_\rho}} \\ && \mathbf{B}\mathfrak{h}_1 } \,.$$

In the simple analogous situation of Lie groupoids this comes about as follows (see at geometry of physics – representations and associated bundles for detailed lecture notes on the following):

for $H$ a Lie group and $\rho$ a smooth action of $H$ on some smooth manifold $V$, then there is the action groupoid $V/H$. Its objects are the points of $V$, but then it has morphisms of the form $v \stackrel{h}{\longrightarrow} \rho(h)(v)$ connecting any two objects that are taken to each other by the Lie group action. For example when $V = \ast$ is the point, then $\ast/H \simeq \mathbf{B}H$ is just the one-object delooping Lie groupoid of the Lie group $H$ itself. This also shows that there is canonical map

$$\array{ && V/H \\ & \swarrow \\ \mathbf{B}H }$$

which is given by sending all $v\in V$ to the point, and sending each morphism $v \stackrel{h}{\longrightarrow} \rho(h)(v)$ to $\ast \stackrel{h}{\longrightarrow} \ast$.

This projection is evidently an isofibration, meaning that if we have a morphism in $\mathbf{B}G$ and a lift of its source object to $V/H$, then there is a compatible lift of the whole morphism. This is a technical condition which ensures that the ordinary fiber of this morphism is equivalently already it homotopy fiber. But the ordinary fiber of this morphisms, hence the stuff in $V/H$ that gets send to the (identity morphism on) the point, is clearly just $V$ itself again. Hence we conclude that the action of $G$ on $V$ induced a homotopy fiber sequence

$$\array{ && V \\ && \downarrow \\ && V/H \\ & \swarrow \\ \mathbf{B}H } \,.$$

With a little more work one may show that every homotopy fiber sequence of this form is induced this way by an action, up to equivalence. Hence actions of $H$ are equivalently bundles over $\mathbf{B}H$. One way to understand this is to observe that the action groupoid $V/H$ is a model for the homotopy quotient of the action, and by the Borel construction this may equivalently be written as the $\rho$-associated bundle to the $H$-universal principal bundle:

$$V/H \simeq \mathbf{E}H \underset{\rho}{\times} V \,.$$

Hence the statement is that the map that sends $H$-actions $\rho$ the universal $\rho$-associated bundle is an equivalence, not just in the context of Lie groups andLie groupoids but much more generally (in every “(infinity,1)-topos”).

Again back now to the analogous situation with $L_\infty$-algebras instead of Lie groups, a second fact which we are to invoke then is that given $\rho$, then the $\infty$-equivariance of $\mu_2$ is equivalent to it descending down the homotopy fibers on both sides to an $L_\infty$-homomorphism of the form

$$\mu_2/\mathfrak{h}_1 \;\colon\; \mathfrak{g} \longrightarrow (\mathbf{B}\mathfrak{h}_2)/\mathfrak{h}_1$$

making this diagram commute in the homotopy category:

$$\array{ \hat \mathfrak{g} && \stackrel{\mu_2}{\longrightarrow} && \mathbf{B}\mathfrak{h}_2 \\ {}^{\mathllap{hofib(\mu_1)}}\downarrow && && \downarrow^{\mathrlap{hofib(p_\rho)}} \\ \mathfrak{g} && \stackrel{\mu_2/\mathfrak{h}_1}{\longrightarrow} && (\mathbf{B}\mathfrak{h}_2)/\mathfrak{h}_1 \\ & {}_{\mathllap{\mu_1}}\searrow && \swarrow_{\mathrlap{p_\rho}} \\ && \mathbf{B}\mathfrak{h}_1 } \,.$$

In our example of Lie group principal bundles this comes down to a classical statement:

one may explicitly check that a morphism of the form

$$\array{ X && \stackrel{\sigma}{\longrightarrow} && V/H \\ & \searrow && \swarrow \\ && \mathbf{B}H }$$

is equivalently a section of the $V$-fiber bundle which is associated via $\rho$ to the $H$-principal bundle that is classified by the map on the left. If we pass this to the iterated homotopy fibers (the Cech nerve) of the vertical maps

$$\array{ P \underset{X}{\times}P \simeq P \times H && \longrightarrow && V \times H \\ \downarrow\downarrow && && \downarrow \downarrow \\ P && \stackrel{\tilde \sigma}{\longrightarrow} && V \\ \downarrow && && \downarrow \\ X && \stackrel{\sigma}{\longrightarrow} && V/H \\ & \searrow && \swarrow \\ && \mathbf{B}H }$$

then this $\sigma$ induces a $V$-valued function on the total space $P$ of the principal bundle with the property that this is $G$-equivariant. It is a classical fact that such equivariant $V$-valued functions on total spaces of principal bundles are equivalent to sections of the associated $V$-fiber bundles. What we are claiming and using here is that this fact again holds in vastly more generality, namely in an (infinity,1)-topos.

In conclusion:

Remark

The resulting triangle diagram

$$\array{ \mathfrak{g} && \stackrel{\mu_2/\mathfrak{h}_1}{\longrightarrow} && (\mathbf{B}\mathfrak{h}_2)/\mathfrak{h}_1 \\ & {}_{\mathllap{\mu_1}}\searrow && \swarrow_{\mathrlap{p_\rho}} \\ && \mathbf{B}\mathfrak{h}_1 }$$

regarded as a morphism

$$\mu_2/\mathfrak{h}_1 \;\colon\; \mu_{1} \longrightarrow p_rho$$

in the slice over $\mathbf{B}\mathfrak{h}_1$ exhibits $\mu_2/\mathfrak{h}_1$ as a cocycle in (rational) $\mu_1$-twisted cohomology with respect to the local coefficient bundle $p_\rho$.

(Nikolaus-Schreiber-Stevenson 12)

Notice that a priori this is (twisted) nonabelian cohomology, though it may happen to land in abelian-, i.e. stable-cohomology.

Such descent is what one needs to find for the brane bouquet above, in order to interpret each of its branches as encoding $p$-brane model on spacetime itself. This is a purely algebraic problem which has been solved (Fiorenza-Sati-Schreiber 15). We discuss the solution in a moment.

The higher WZW terms of super $p$-branes

Open problem:

$\;\;$ Understand M-theory from first principles, not via perturbative string theory.

Theorem reviewed here:

$\;\;$Much of the known/expected structure of M-theory

$\;\;$follows from analysis of the superpoint

$\;\;$in super Lie n-algebra homotopy theory.

Based on Fiorenza-Sati-Schreiber 13, 16a, 16b.

$\,$

If history is a good guide, then we should expect that anything as profound and far-reaching as a fully satisfactory formulation of M-theory is surely going to lead to new and novel mathematics. Regrettably, it is a problem the community seems to have put aside - temporarily. But, ultimately, Physical Mathematics must return to this grand issue. (G. Moore, p. 45 of “Physical Mathematics and the Future”, talk at Strings 2014)

Spacetime

Everything we say below follows

by developing this elementary phenomenon (highlighted in Schreiber 15):

Proposition

Consider the superpoint

$$\;\;\;\;\;\; \mathbb{R}^{0\vert 1}$$

regarded as an abelian super Lie algebra.

Its maximal central extension is

the $N = 1$ super-worldline of the superparticle:

$$\array{ \mathbb{R}^{0,1\vert \mathbf{1}} \\ \downarrow \\ \mathbb{R}^{0\vert 1} } \,.$$

• whose even part is spanned by one generator $H$

• whose odd part is spanned by one generator $Q$

• the only non-trivial bracket is

  $$\{Q, Q\} = H$$

Then consider the superpoint

$$\;\;\;\;\;\; \mathbb{R}^{0\vert 2} \,.$$

Its maximal central extension is

the $d = 3$, $N = 1$ super Minkowski spacetime

$$\array{ \mathbb{R}^{2,1\vert \mathbf{2}} \\ \downarrow \\ \mathbb{R}^{0\vert 2} } \,.$$

• whose even part is $\mathbb{R}^3$, spanned by generators $P_0, P_1, P_2$

• whose odd part is $\mathbb{R}^2$, regarded as

  the Majorana spinor representation $\mathbf{2}$

  of $Spin(2,1) \simeq SL(2,\mathbb{R})$

• the only non-trivial bracket is the spinor bilinear pairing

  $$\{Q_\alpha, Q'_\beta\} = C_{\alpha \alpha'} \Gamma_a{}^{\alpha'}{}_\beta \,P^a$$

where $C_{\alpha \beta}$ is the charge conjugation matrix.

Proof

$\,$

Recall that

$d$-dimensional central extensions of super Lie algebras $\mathfrak{g}$

are classified by 2-cocycles.

These are super-skew symmetric bilinear maps

$$\mu_2 \;\colon\; \mathfrak{g} \wedge\mathfrak{g} \longrightarrow \mathbb{R}^d$$

satisfying a cocycle condition.

The extension $\widehat{\mathfrak{g}}$ that this classifies

has underlying super vector space

the direct sum

$$\widehat{\mathfrak{g}} \coloneqq \mathfrak{g} \oplus \mathbb{R}^d$$

an the new super Lie bracket is given

on pairs $(x,c) \in \mathfrak{g} \oplus \mathbb{R}^d$

by

$$[\; (x_1,c_1), (x_2,c_2)\;]_{\mu_2} \;=\; (\, [x_1,x_2]\,,\, \mu_2(c_1,c_2) \,) \,.$$

The condition that the new bracket $[-,-]_{\mu_2}$ satisfies the super Jacobi identity

is equivalent to the cocycle condition on $\mu_2$.

Now

in the case that $\mathfrak{g} = \mathbb{R}^{0\vert q}$,

then the cocycle condition is trivial

and a 2-cocycle is just a symmetric bilinear form

on the $q$ fermionic dimensions.

So

in the case $\mathfrak{g} = \mathbb{R}^{0\vert 1}$

there is a unique such, up to scale, namely

$$\mu_2(a Q,b Q) = a b P \,.$$

But

in the case $\mathfrak{g} = \mathbb{R}^{0\vert 2}$

there is a 3-dimensional space of 2-cocycles, namely

$$\mu_2 \left( \left( \array{ Q_1 \\ Q_2 }\right), \left( \array{ Q'_1 \\ Q'_2 } \right) \right) = \left\{ \array{ Q_1 Q'_1, & \tfrac{1}{2}\left( Q_1 Q'_2 + Q_2 Q'_1 \right), \\ & Q_2 Q'_2 } \right.$$

If this is identified with the three coordinates

of 3d Minkowski spacetime

$$\mathbb{R}^{2,1} \;\simeq\; \left( \array{ t + x & y \\ & t - x } \right)$$

then the pairing is the claimed one

(see at supersymmetry – in dimensions 3,4,6,10).

$\,$

This phenomenon continues:

$\,$

Theorem

(J. Huerta)

The diagram of super Lie algebras shown on the right

is obtained by consecutively forming

maximal central extensions

invariant with respect to

the maximal subgroup of automorphisms

for which there are invariant cocycles at all.

Here $\mathbb{R}^{d-1,1\vert \mathbf{N}}$

is the $d$, $\mathbf{N}$ super-translation supersymmetry algebra.

And these subgroups are

the spin group covers $Spin(d-1,1)$

of the Lorentz groups $O(d-1,1)$.

$\,$

Side remark: That every super Minkowski spacetime is some central extension of some superpoint is elementary. This was highlighted in (Chryssomalakos-Azcárraga-Izquierdo-Bueno 99, 2.1). But most central extensions of superpoints are nothing like super-Minkowksi spacetimes. The point of the above proposition is to restrict attention to iterated invariant central extensions and to find that these single out the super-Minkoski spacetimes.

$\,$

Conclusion:

Just from studying iterated invariant central extensions

of super Lie algebras,

starting with the superpoint,

we (re-)discover

1. Lorentzian geometry,

2. spin geometry.

3. super spacetimes.

$\,$

May we extend further?

$\,$

Branes

$\,$

There are no further invariant 2-cocycles on

But there is an invariant 3-cocycle.

$\,$

There are no further invariant 2-cocycles on $\mathbb{R}^{10,1\vert \mathbf{32}}$

But there is an invariant 4-cocycle.

$\,$

So:

What are higher super Lie algebra cocycles?

And what kind of extensions do they classify?

$\,$

Quick answer:

Higher cocycles are closed elements in a Chevalley-Eilenberg algebra.

They classify super Lie-∞ algebra extensions.

$\,$

This we explain now.

$\,$

Definition

For $\mathfrak{g}$ a super Lie algebra

of finite dimension,

then its Chevalley-Eilenberg algebra $CE(\mathfrak{g})$

is the super-Grassmann algebra on the dual super vector space

$$\wedge^\bullet \mathfrak{g}^\ast$$

equipped with a differential $d_{\mathfrak{g}}$

that on generators is the linear dual of the super Lie bracket

$$d_{\mathfrak{g}} \coloneqq [-,-]^\ast \;\colon\; \mathfrak{g}^\ast \to \mathfrak{g}^\ast \wedge \mathfrak{g}^\ast$$

and which is extended to $\wedge^\bullet \mathfrak{g}^\ast$

by the graded Leibniz rule (i.e. as a graded derivation).

$\,$

Here all elements are $(\mathbb{Z} \times \mathbb{Z}/2)$-bigraded,

the first being the cohomological grading $n$ in $\wedge^\n \mathfrak{g}^\ast$,

the second being the super-grading $\sigma$ (even/odd).

The sign rule is

$$\alpha \wedge \beta = (-1)^{n_1 n_2} (-1)^{\sigma_1 \sigma_2}\; \beta \wedge \alpha \,.$$

A $(p+2)$-cocycle on $\mathfrak{g}$

is an element of degree $(p+2,0)$ in $CE(\mathfrak{g})$

which is $d_{\mathbb{g}}$ closed. It is non-trivial if it is not $d_{\mathfrak{g}}$-exact.

$\,$

We may think of $CE(\mathfrak{g})$ equivalently

as the dg-algebra of left-invariant super differential forms

on the corresponding simply connected super Lie group .

$\,$

Example

For $d \in \mathbb{N}$

and $\mathbf{N}$ a Majorana spin representation of $Spin(d-1,1)$

then the super-translation supersymmetry super Lie algebra $\mathbb{R}^{d-1,1\vert \mathbf{N}}$

has Chevalley-Eilenberg algebra generated by

• $\{e^a\}_{a = 0}^{d-1}$ in bi-degree $(1,even)$;

• $\{\psi_\alpha\}_{\alpha = 1}^N$ in bi-degree $(1,odd)$.

with differential

$$d \;:\; \left\{ \array{ \psi_\alpha &\mapsto& 0 \\ e^a & \mapsto & \overline{\psi} \wedge \Gamma^a \psi } \right.$$

where

$$\overline{(-)}\Gamma^a(-) = (-)^\dagger \Gamma^0 \Gamma^a (-)$$

is the standard spinor bilinear pairing

in the spin representation $\mathbf{N}$.

$\,$

If we think of super Minkowski spacetime

as the supermanifold with

• even coordinates $\{x^a\}_{a = 0}^{d-1}$;

• odd coordinates $\{\theta_\alpha\}_{\alpha = 1}^N$

then these generators correspond to these super differential forms:

$$\begin{aligned} e^a & = d_{dR} x^a + \underset{\text{correction term}}{\underbrace{\overline{\theta} \Gamma^a d_{dR} \theta}} \\ \psi^\alpha & = d_{dR} \theta^\alpha \end{aligned}$$

the super-vielbein.

$\,$

Notice that $d_{dR} x^a$ alone

fails to be a left invariant differential form,

in that it is not annihilated by the supersymmetry

vector fields

$$D_\alpha \;\coloneqq\; \partial_{\theta^\alpha} - \overline{\theta}_{\alpha'} \Gamma^a{}^{\alpha'}{}_\alpha \partial_{x^a}\,.$$

Therefore the all-important correction term above.

$\,$

Example

$\,$

The 2-cocycle that classifies the extension

$$\array{ \mathbb{R}^{10,1\vert \mathbf{32}} && 11d, N = 1 \\ \downarrow \\ \mathbb{R}^{9,1\vert \mathbf{16}+ \overline{\mathbf{16}}} && 10d, \text{type IIA} }$$

is

$$i \, \overline{\psi} \wedge \Gamma_{11} \psi \;\in\; CE(\mathbb{R}^{9,1\vert \mathbf{16}+ \overline{\mathbf{16}}})$$

Regarded as a 2-form on $\mathbb{R}^{9,1\vert \mathbf{32}}$,

this is the curvature of the WZW-term

in the Green-Schwarz sigma-model for the D0-brane.

See below.

$\,$

Proposition

(Achúcarro-Evans-Townsend-Wiltshire 87, Brandt 12-13)

The maximal invariant 3-cocycle on 10d super Minkowski spacetime is

$$\mu_{F1} = \left(\overline{\psi} \wedge \Gamma_a \psi\right) \wedge e^a$$

This is the WZW term for the Green-Schwarz superstring (Green-Schwarz 84).

The maximal invariant 4-cocycle on super Minkowski spacetime is

$$\mu_{M2} = i \left(\overline{\psi} \wedge \Gamma_{a b} \psi \right) \wedge e^a \wedge e^b$$

This is the higher WZW term for the supermembrane (Bergshoeff-Sezgin-Townsend 87).

This classification is also known as

the old brane scan.

$\,$

Here “higher WZW term” means the following:

$\,$

Regard $\mu_{F1} = \left(\overline{\psi} \wedge \Gamma_a \psi\right) \wedge e^a$

as a left invariant differential form

on super-Minkowski spacetime.

Choose any differential form potential $B_{F1}$

i.e. such that

$$d_{dR} B_{F1} = \left(\overline{\psi} \wedge \Gamma_a \psi\right) \wedge e^a \,.$$

(This $B_{F1}$ will not be left-invariant.)

Then the Green-Schwarz action functional for the superstring

is the function on the space of sigma-model fields

$$\phi \;\colon\; \underset{\text{worldsheet}}{\underbrace{\Sigma_2}} \longrightarrow \underset{\text{super-spacetime}}{\underbrace{\mathbb{R}^{9,1\vert \mathbf{N}}}}$$

(morphisms of supermanifolds)

given by

$$\phi \;\mapsto\; \underset{\text{kinetic action}}{ \underbrace{ \int_{\Sigma_2} \sqrt{ -det(\partial_{\sigma^i} e^a(\phi) \partial_{\sigma_j} e_b(\phi)) } \, d \sigma^1 \wedge d\sigma^2 }} + \underset{\text{WZW term}}{ \underbrace{ \int_{\Sigma^2} \phi^\ast B_{F1} } } \,.$$

The first term is the Nambu-Goto action

the second is a WZW term.

$\,$

Originally Green-Schwarz 84 introduced $B_{F1}$

to ensure an additional fermionic symmetry: “kappa-symmetry”.

Notice that $B_{F1}$ looks somewhat complicated

and is not unique.

That it is simply a WZW-term

for the supersymmetry supergroup

$$\mathbb{R}^{9,1\vert \mathbf{N}} = Iso(\mathbb{R}^{9,1\vert \mathbf{N}}) / Spin(9,1)$$

was observed in Henneaux-Mezincescu 85.

$\,$

Similarly,

choose any differential form potential $C_{M2}$ such that

$$d_{dR} C_{M2} = \left(\overline{\psi} \wedge \Gamma_{a b} \psi\right) \wedge e^a \wedge e^b \,.$$

(This $C_{M2}$ will not be left-invariant.)

Then the Green-Schwarz type action functional

for the supermembrane

is the function on sigma-model fields

$$\phi \;\colon\; \underset{\text{worldvolume}}{\underbrace{\Sigma_3}} \longrightarrow \mathbb{R}^{10,1\vert \mathbf{32}}$$

given by

$$\phi \;\mapsto\; \underset{\text{kinetic action}}{ \underbrace{ \int_{\Sigma_2} \sqrt{ -det(\partial_{\sigma^i} e^a(\phi)\partial_{\sigma_j} e_b(\phi)) } \, d \sigma^1 \wedge d\sigma^2 \wedge d\sigma^3 }} + \underset{\text{WZW term}}{ \underbrace{ \int_{\Sigma^3} \phi^\ast C_{M2} } } \,.$$

On the right this is

the higher WZW term.

$\,$

Now we discuss that higher cocycles classify higher extensions:

$\,$

First observe that

Proposition

Homomorphisms of super Lie algebras

$$\mathfrak{g}_1 \longrightarrow \mathfrak{g}_2$$

are in natural bijection with the homomorphisms of dg-algebras

between their Chevalley-Eilenberg algebra, going the opposite direction:

$$CE(\mathfrak{g}_1) \longleftarrow CE(\mathfrak{g}_2) \,.$$

This means that we may identify super Lie algebras with their CE-algebras.

In the terminology of category theory: the functor

$$CE \;\colon\; s LieAlg_{\mathbb{R}} \hookrightarrow dgAlg_{\mathbb{R}}^{op}$$

given by

$$\mathfrak{g} \mapsto CE(\mathfrak{g}) = (\wedge^\bullet \mathfrak{g}^\ast, [-,-]^\ast)$$

is fully faithful.

$\,$

Therefore is natural to make the following definition.

$\,$

Definition

A super Lie-infinity algebra of finite type is

1. a $\mathbb{Z}$-graded super vector space $\mathfrak{g}$

   degreewise of finite dimension

2. for all $n \geq 1$ a multilinear map

   $$[-,\cdots, -] \;\colon\; \wedge^n \mathfrak{g} \longrightarrow \wedge^1 \mathfrak{g}$$

   of degree $(-1,even)$

such that

the graded derivation on the super-Grassmann algebra $\wedge^\bullet \mathfrak{g}^\ast$ given by

$$d_{\mathfrak{g}} \coloneqq [-]^\ast + [-,-]^\ast + [-,-,-]^\ast + \cdots \;\; \colon\;\; \wedge^1 \mathfrak{g}^\ast \longrightarrow \wedge^\bullet \mathfrak{g}^\ast$$

squares to zero:

$$d_{\mathfrak{g}} d_{\mathfrak{g}} = 0$$

and hence defines a dg-algebra

$$CE(\mathfrak{g}) \coloneqq ( \wedge^\bullet \mathfrak{g}^\ast, d_{\mathfrak{g}} ) \,.$$

A homomorphism of super $L_\infty$-algebras is dually a homomorphism of their CE-algebras.

$\,$

If $\mathfrak{g}$ is concentrated

in degrees $0$ to $n-1$

we call it a super Lie n-algebra.

$\,$

Side remark:

We may drop the assumption of degreewise finiteness

by regarding $\vee^\bullet \mathfrak{g}$ as a free graded co-commutative coalgebra

and $D \coloneqq [-] + [-,-] + [-,-,-] + \cdots$ as a differential

making a differential graded coalgebra.

$\,$

$L_\infty$-algebras in the sense of def. were introduced in Lada-Stasheff 92.

That they are fully characterized

by their Chevalley-Eilenberg dg-(co-)algebras

is due to Lada-Markl 94.

See Sati-Schreiber-Stasheff 08, around def. 13.

$\,$

But in fact the CE-algebras of super $L_\infty$-algebras of finite type

were implicitly introduced

as tools for the higher super Cartan geometry of supergravity

already in D’Auria-Fré 82 (see D'Auria-Fré formulation of supergravity)

where they were called FDAs.

higher Lie theory	supergravity
$\,$ super Lie n-algebra $\mathfrak{g}$ $\,$	$\,$ “FDA” $CE(\mathfrak{g})$ $\,$

$\,$

However,

what has not been used in the “FDA” literature

is that $L_\infty$-algebras are objects in homotopy theory:

$\,$

Proposition

(Pridham 10, prop. 4.36)

There exists a model category such that

1. its fibrant objects are the (super-)L-∞ algebras

   with the above homomorphisms between them;

2. and

   • the weak equivalences between (super-)$L_\infty$-algebras are the quasi-isomorphisms;

   • fibrations between (super-)$L_\infty$-algebras are the surjections

   on the underlying chain complex (using the unary part of the differential).

For more see at model structure for L-infinity algebras.

$\,$

Concretely,

this implies in particular that

every homomorphisms of super L-∞ algebras

$$\array{ \mathfrak{g}_1 \\ & {}_{\mathllap{f}}\searrow \\ && \mathfrak{g}_2 }$$

is the composite of a quasi-isomorphism followed by a surjection

$$\array{ \mathfrak{g}_1 && \overset{\text{quasi-iso}}{\longrightarrow} && \widetilde \mathfrak{g}_1 \\ & {}_{\mathllap{f}}\searrow && \swarrow_{\mathrlap{ {f_{fib}} \atop {\text{surjection}}}} \\ && \mathfrak{g}_2 } \,.$$

That surjective homomorphism $f_{fib}$

is called a fibrant replacement of $f$.

$\,$

Definition

Given homomorphisms of super L-∞ algebras

$$\mathfrak{g}_1 \overset{f}{\longrightarrow} \mathfrak{g}_2$$

then its homotopy fiber $hofib(f)$

is the kernel of any fibrant replacement

$$hofib(f) \;\coloneqq\; ker(f_{fib}) \,.$$

Standard facts in homotopy theory assert

that $hofib(f)$ is well-defined

up to quasi-isomorphism.

See at Introduction to homotopy theory – Homotopy fibers.

$\,$

Proposition

(Fiorenza-Sati-Schreiber 13, prop. 3.5)

Write

$$B^{p+1}\mathbb{R}$$

for the line Lie (p+1)-algebra, given by

$$CE(B^{p+1}\mathbb{R}) \;=\; \left( \wedge^\bullet \underset{\text{single generator} \atop \text{in deg.} \, (p+2,even)}{\underbrace{\langle c_{p+2} \rangle}} \;,\; d_{B^{p+1}\mathbb{R}} = 0 \right) \,.$$

A $(p+2)$-cocycle on an $L_\infty$-algebra is equivalently a homomorphim

$$\mu_{p+2} \;\colon\; \mathfrak{g} \longrightarrow B^{p+1}\mathbb{R} \,.$$

The homotopy fiber of this map

$$\array{ \widehat{\mathfrak{g}} \\ {}^{\mathllap{hofib(\mu_{p+2})}}\downarrow \\ \mathfrak{g} &\underset{\mu_{p+2}}{\longrightarrow}& B^{p+1}\mathbb{R} }$$

is given by adjoining to $CE(\mathfrak{g})$ a single generator $b_{p+1}$

forced to be a potential for $\mu_{p+2}$:

$$CE(\widehat{\mathfrak{g}}) \;\simeq\; CE(\mathfrak{g})[b_{p+1}]/(d b_{p+1} = \mu_{p+2}) \,.$$

Example

$\,$

The homotopy fiber of a 2-cocycle

is the classical central extension

that it classifies.

$\,$

Conclusion.

$\;\;$ The higher central extensions

$\;\;$ classified by higher cocycles

$\;\;$ are their homotopy fibers.

$\,$

This way we may finally continue

the progression of invariant central extensions

to higher central extensions:

$\,$

Definition

$\,$

Name the homotopy fibers of the cocycles

which are the higher WZW terms

of the superstring and the supermembrane

as follows

$$\array{ \mathfrak{m}2\mathfrak{brane} \\ {}^{\mathllap{hofib}(\mu_{M2})}\downarrow \\ \mathbb{R}^{10,1\vert \mathbf{32}} &\underset{\mu_{M2}}{\longrightarrow}& B^3 \mathbb{R} }$$

$\,$

$\,$

$$\array{ \mathfrak{string}_{IIB} \\ {}^{\mathllap{hofib}(\mu_{F1}^B)}\downarrow \\ \mathbb{R}^{9,1\vert \mathbf{16}+ \mathbf{16}} &\underset{\mu_{F1}^B}{\longrightarrow}& B^2 \mathbb{R} } \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \array{ \mathfrak{string}_{het} \\ {}^{\mathllap{hofib}(\mu_{F1}^{het})}\downarrow \\ \mathbb{R}^{9,1\vert \mathbf{16}} &\underset{\mu_{F1}^{het}}{\longrightarrow}& B^2 \mathbb{R} } \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \array{ \mathfrak{string}_{IIA} \\ {}^{\mathllap{hofib}(\mu_{F1}^A)}\downarrow \\ \mathbb{R}^{9,1\vert \mathbf{16}+ \overline{\mathbf{16}}} &\underset{\mu_{F1}^A}{\longrightarrow}& B^2 \mathbb{R} }$$

$\,$

The super Lie 2-algebra $\mathfrak{string}_{het}$ is given by

$$CE(\mathfrak{string}_{het}) = \left\{ \array{ d e^a = \overline{\psi} \Gamma^a \psi, \; d \psi^\alpha = 0 \\ d b_2 = \mu_{F1}^{het} = (\overline{\psi} \wedge \Gamma_a \psi)\wedge e^a } \right\}$$

This is a super-version of the string Lie 2-algebra (Baez-Crans-Schreiber-Stevenson 05

which controls Green-Schwarz anomaly cancellation (Sati-Schreiber-Stasheff 12)

and the topology of the supergravity C-field (Fiorenza-Sati-Schreiber 12a, 12b).

$\,$

The membrane super Lie 3-algebra $\mathfrak{m}2\mathfrak{brane}$ is given by

$$CE(\mathfrak{m}2\mathfrak{brane}) = \left\{ \array{ d e^a = \overline{\psi} \wedge \Gamma^a \psi, \; d \psi^\alpha = 0 \\ d b_3 = i (\overline{\psi} \wedge \Gamma_{a b} \psi) \wedge e^a \wedge e^b } \right\}$$

This dg-algebra was first considered in D’Auria-Fré 82 (3.15)

as a tool for constructing 11-dimensional supergravity.

For exposition from the point of view of Lie 3-algebras see also Baez-Huerta 10.

$\,$

Hence the progression

of maximal invariant extensions of the superpoint

continues as a diagram

of super L-∞ algebras like so:

$\,$

$\,$

(While every extension displayed is a maximal invariant higher central extension, not all invariant higher central extensions are displayed. For instance there are string and membrane GS-WZW-terms / cocycles also on the lower dimensional super-Minkowski spacetimes (“non-critical”), e.g. the super 1-brane in 3d and the super 2-brane in 4d.)

$\,$

The “old brane scan” ran into a conundrum:

Given that superstrings and supermembranes

are nicely classified by super Lie algebra cohomology

why do the other super p-branes not show up similarly?

Where are the D-branes and the M5-brane?

$\,$

But now we see that we should look for

further higher cocycles

not on super Lie algebras

but on super L-∞ algebras.

$\,$

Proposition

(Chryssomalakos-Azcárraga-Izquierdo-Bueno 99, Sakaguchi 99, Fiorenza-Sati-Schreiber 13)

The higher WZW terms for the D-branes

are invariant super $L_\infty$-cocycles

on the higher extended super Minkowski spacetimes from above

$$\mu_{D p} \;\colon\; \mathfrak{string} \stackrel{\phantom{AAAAAAAA}}{\longrightarrow} B^{p+1}\mathbb{R} \,.$$

Similarly,

the higher WZW term for the M5-brane

is an invariant super $L_\infty$ 7-cocycle

of the form

$$\mu_{M5} \;\colon\; \mathfrak{m}2\mathfrak{brane} \stackrel{\phantom{AAAAAAAAA}}{\longrightarrow} B^6 \mathbb{R} \,.$$

$\,$

By the above, these cocycles classify

further higher super $L_\infty$-algebra extensions

$$\array{ \mathfrak{d}p\mathfrak{brane} \\ {}^{\mathllap{hofib(\mu_{D p})}}\downarrow \\ \mathfrak{string}_{IIA/B} &\underset{\mu_{D p}}{\longrightarrow}& B^{p+1}\mathbb{R} } \;\;\;\;\;\;\;\;\,\;\;\;\;\;\;\;\;\;\;\; \array{ \mathfrak{m}5\mathfrak{brane} \\ {}^{\mathllap{hofib(\mu_{M5})}}\downarrow \\ \mathfrak{m}2\mathfrak{brane} &\underset{\mu_{M5}}{\longrightarrow}& B^6 \mathbb{R} }$$

$\,$

Notice that all these are higher cocycles

except for that of the D0-brane, which is just a 2-cocycle.

The ordinary central extension that this classifies

is just that which grows the 11th M-theory dimension by the above example .

$$\array{ \mathbb{R}^{10,1\vert \mathbf{32}} \\ {}^{\mathllap{hofib(\mu_{D0})}} \downarrow \\ \mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}} &\underset{\mu_{D0} = i \, \overline{\psi} \Gamma_{11} \psi }{\longrightarrow}& B \mathbb{R} }$$

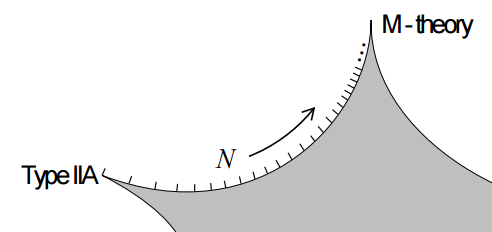
This may be thought of

as a super $L_\infty$-theoretic incarnation

of D0-brane condensation

(Polchinski 99, around p. 8).

$\,$

In conclusion:

by forming

iterated (maximal) invariant higher central super $L_\infty$-extensions

of the superpoint,

we obtain the following “brane bouquet”

$\,$

$\,$

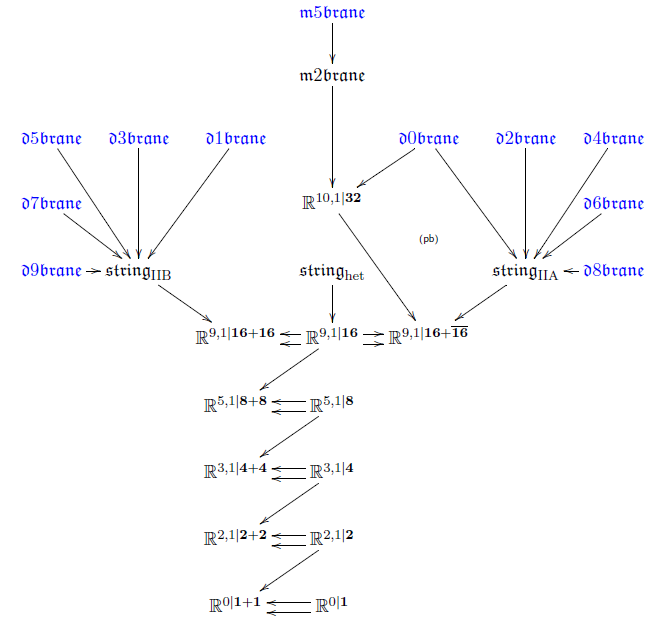
Each object in this diagram of super L-∞ algebras

is a super spacetime or super p-brane of string theory / M-theory.

$\,$

Moreover, this diagram knows the brane intersection laws:

there is a morphism $p_2\mathfrak{brane} \longrightarrow p_1 \mathfrak{brane}$

precisely if the given species of $p_1$-branes may end on the given species of $p_2$-branes

(more discussion of this is in Fiorenza-Sati-Schreiber 13, section 3).

$\,$

Perhaps we need to understand the nature of time itself better. $[...]$ One natural way to approach that question would be to understand in what sense time itself is an emergent concept, and one natural way to make sense of such a notion is to understand how pseudo-Riemannian geometry can emerge from more fundamental and abstract notions such as categories of branes. (G. Moore, p.41 of “Physical Mathematics and the Future”, talk at Strings 2014)

$\,$

But how are we to think of the extended super Minkowski spacetimes geometrically?

This is clarified by the following result:

$\,$

Proposition

(Fiorenza-Sati-Schreiber 13, section 5)

Write $\widetilde {String_{IIA}}$ for the super 2-group

that Lie integrates the super Lie 2-algebra $\mathfrak{string}_{IIA}$

subject to the condition that it carries a globally defined Maurer-Cartan form.

Then for $\Sigma_{p+1}$ a worldvolume smooth manifold

there is a natural equivalence

$$\left\{ \Sigma_{p+1} \stackrel{\Phi}{\longrightarrow} \widetilde{String_{IIA}} \right\} \;\;\; \leftrightarrow \;\;\; \left\{ \array{ \Sigma_{p+1} \stackrel{\phi}{\longrightarrow} \mathbb{R}^{9,1\vert \mathbf{16}+ \overline{\mathbf{16}} }, \\ \nabla \in Conn(\Sigma_{p+1}, \phi^\ast \mu_{string_{IIA}} ) } \right\}$$

between “higher Sigma-model fields” $\Phi$

and pairs, consisting of

an ordinary sigma-model field $\phi$

and a gauge field $\nabla$ on the worldvolume of the D-brane

twisted by the Kalb-Ramond field.

This is the Chan-Paton gauge field on the D-brane.

$\,$

Similarly:

Write $\widetilde {M2Brane}$ for the super 3-group

that Lie integrates the super Lie 3-algebra $\mathfrak{m}2\mathfrak{brane}$

subject to the condition that it carries a globally defined Maurer-Cartan form.

Then for $\Sigma_{5+1}$ a worldvolume smooth manifold

there is a natural equivalence

$$\left\{ \Sigma_{5+1} \stackrel{\Phi}{\longrightarrow} \widetilde{M2Brane} \right\} \;\;\; \leftrightarrow \;\;\; \left\{ \array{ \Sigma_{5+1} \stackrel{\phi}{\longrightarrow} \mathbb{R}^{10,1\vert \mathbf{32} }, \\ \nabla \in 2Conn(\Sigma_{p+1}, \phi^\ast \mu_{M2} ) } \right\}$$

between “higher Sigma-model fields” $\Phi$

and pairs, consisting of

an ordinary sigma-model field $\phi$

and a higher gauge field $\nabla$ on the worldvolume of the M5-brane

and twisted by the supergravity C-field.

$\,$

(See also at Structure Theory for Higher WZW Terms, session II).

$\,$

In conclusion this shows that

given a cocycle $\mu_{p_1+2}$ for some super $p_1$-brane species

inducing an extended super Minkowski spacetime via its homotopy fiber

and then given a consecutive cocycle $\mu_{p_2+2}$ for a $p_2$-brane species on that homotopy fiber

then $p_1$-branes may end on $p_2$-branes

and the $p_2$-branes propagating in the extended spacetime $p_1 \mathfrak{brane}$

see a higher gauge field on their worldvolume

of the kind sourced by boundaries of $p_1$-branes.

$\,$

$$\array{ { \text{spacetime} \atop \text{with}\,p_1\text{-brane condensate} } && p_1 \mathfrak{brane} &\overset{\mu_{p_2+2}}{\longrightarrow}& B^{p_2+2} \\ && {\mathllap{hofib(\mu_{p_1+2})}}\downarrow \\ \text{spacetime} && \mathbb{R}^{d-1,1\vert \mathbf{N}} &\underset{\mu_{p_1+2}}{\longrightarrow}& B^{p_1+1}\mathbb{R} }$$

$\,$

Hence the extended super Minkowski spacetime $p_1 \mathfrak{brane}$

is like the original super spacetime $\mathbb{R}^{d-1,1\vert \mathbf{N}}$

but filled with a condensate of $p_1$-branes

whose boundaries source a higher gauge field.

$\,$

While this is good,

it means that at each stage of the brane bouquet

we are describing $p_2$-brane dynamics

on a fixed $p_1$-brane background field.

But more generally

we would like to describe the joint dynamics

of all brane species at once.

$\,$

This we turn to now.

$\,$

Fields

We now discuss that

$\;\;\;\;$There is homotopy descent of $p$-brane WZW terms

$\;\;\;\;$from extended super Minkowski spacetime

$\;\;\;\;$down to ordinary super Minkowski spacetime

$\;\;\;\;$which yields cocycles in twisted cohomology

$\;\;\;\;$for the RR-field and the M-flux fields.

(Fiorenza-Sati-Schreiber 15, 16a).

$\,$

In order to explain this we now first recall

the general nature of twisted cohomology

and its role in string theory.

$\,$

Twisted generalized cohomology

$\,$

It is often stated that a

Chan-Paton gauge field on $n$ coincident D-branes

is an SU(n)-vector bundle $V$,

hence a cocycle in nonabelian cohomology in degree 1.

$\,$

But this is not quite true.

In general there are $n$ D-branes and $n'$ anti-D-branes coinciding,

carrying Chan-Paton gauge fields

$V_{brane}$ (of rank $n$) and $V_{\text{anti-brane}}$ (of rank $n'$), respectively,

yielding a pair of vector bundles

$$(V_{\text{brane}}, V_{\text{anti-brane}}) \,.$$

Such pairs are also called virtual vector bundles.

$\,$

But D-branes annihilate with anti-D-branes (Sen 98)

when they have exact opposite D-brane charge,

which here means that they carry the same Chan-Paton vector bundle.

In other words, pairs as above of the special form

$(W,W)$ are equivalent to pairs of the form $(0,0)$.

$$(W,W) \;\sim\; 0 \,.$$

Hene the net Chan-Paton charge of coincident branes and anti-branes

is the equivalence class of $(V_{\text{brane}}, V_{\text{anti-brane}})$

under the equivalence relation which is generated by the relation

$$(V_{\text{brane}} \oplus W\,,\; V_{\text{anti-brane}} \oplus W) \;\sim\; (V_{brane}\,,\; V_{anti-brane})$$

for all complex vector bundles $W$ (Witten 98, Witten 00).

$\,$

The additive abelian group of such equivalence classes of virtual vector bundles

is called the topological K-theory.

$\,$

It follows that also the RR-fields are in K-theory (Moore-Witten 00).

$\,$

Topological K-theory is similar to ordinary cohomology

but is a generalized (Eilenberg-Steenrod) cohomology theory.

A generalized cohomology theory is represented by a spectrum

(in the sense of stable homotopy theory):

A spectrum is sequence of pointed topological spaces

$$E_n \;\;\;\; n \in \mathbb{N}$$

equipped with weak homotopy equivalences

$$E_n \overset{\phantom{AA}\simeq\phantom{AA}}{\longrightarrow} \Omega E_{n+1}$$

from one to the loop space of the next.

$\$

Given this, then the $E$-cohomology of any topological space $X$ is

$$E^n(X) \coloneqq \underset{\text{homotopy classes of maps}}{\underbrace{\pi_0\left\{ X \overset{\phantom{AAAAAA}}{\longrightarrow} E_n \right\} }} \,.$$

For topological K-theory one writes

$$E = KU$$

with

$$KU_{2n} \simeq B U \times \mathbb{Z} \;\;\,,\;\; KU_{2n+1} \simeq U$$

with $U$ the stable unitary group,

and $B U$ the classifying space for complex vector bundles.

$\,$

But above we saw

that the Chan-Paton gauge field on a D-brane

is actually a twisted vector bundle

with twist given by the Kalb-Ramond field

sourced by a string condensate.

(Freed-Witten anomaly cancellation)

$\,$

Such twisted cohomology generalized cohomology is given by

1. a classifying space of twists $B G$

2. a spectrum object in the slice category $Top_{/B G}$, namely a sequence of spaces $E_n/G$ equipped with maps

   $$id \;\colon\; B G \to E_n/G \to B G$$

   and weak equivalences

   $$E_n/G \overset{\phantom{AA}\simeq\phantom{AA} }{\longrightarrow} \Omega_{B G} (E_{n+1}/G) \coloneqq \underset{\text{homotopy} \atop {\text{fiber} \atop \text{product} } }{\underbrace{ B G \underoverset{E_{n+1}/G}{h}{\times} B G }}$$

Extremal examples:

1. an ordinary spectrum $E$

   is a parameterized spectrum over the point;

   $$\array{ E \\ \downarrow \\ \ast }$$

2. an ordinary space $X$

   is identified with the zero-spectrum parameterized over $X$:

   $$\array{ X \\ \downarrow \\ X }$$

Then

1. a twist $\tau$ for $E$-cohomology of $X$ is a map

   $$\array{ X \\ & {}_{\mathllap{\tau}}\searrow \\ && B G }$$

2. the $\tau$-twisted $E$-cohomology of $X$ is

   $$E^{n+\tau}(X) \;\coloneqq\; \pi_0 \left\{ \array{ X && \longrightarrow && E_n/G \\ & {}_{\mathllap{\tau}} \searrow && \swarrow_{\mathrlap{}} \\ && B G } \right\}$$

There is a homotopy fiber sequence (in parameterized spectra)

$$\array{ E &\longrightarrow& E/G \\ && \downarrow \\ && B G }$$

and this equivalently exhibits $E/G$ as the homotopy quotient of an ordinary spectrum $E$ by a $G$-infinity-action.

(Nikolaus-Schreiber-Stevenson 12, section 4.1)

$\,$

Assume that $B G$ is simply connected, i.e. of the form $B^2 G$.

$\,$

We now translate this situation to super L-∞ algebras

via the central theorem of rational homotopy theory.

$\,$

Rational homotopy theory

$\,$

On every loop space $\Omega X$,

the operation of concatenation of loops

gives the structure of a group up to coherent higher homotopy

called a “grouplike A-∞ space”

or ∞-group for short.

$\,$

May recognition theorem:

Conversely, for $G$ an ∞-group

there is an essentially unique connected space $B G$

with $G \;\simeq\; \Omega B G$.

$\,$

Every double loop space $\Omega \Omega X$

becomes a “first order abelian” ∞-group

by exchanging loop directons

called a braided ∞-group,

$\,$

For $G$ a braided ∞-group then

$B G$ is itself an ∞-group

and so there exists an essentially unique simply connected space

$$B^2 G \coloneqq B (B G)$$

with

$$G \;\simeq\; \Omega^2 B^2 G \,.$$

$\,$

And so forth:

Every triple loop space $\Omega^3 X$

becomes a “second order abelian” ∞-group

by exchanging loop directons

called a sylleptic ∞-group.

etc.

$\,$

In a spectrum $E$,

the maps $E_n \stackrel{\simeq}{\to} \Omega E_{n+1}$

exhbit $E_0$ as an infinite loop space

hence as a fully abelian ∞-group.

$\,$

It turns out that by a theoretic version of Lie theory,

there is an L-∞ algebra $\mathfrak{g}$ associated with any ∞-group

$$\mathfrak{g} \simeq \mathfrak{l} B G \,.$$

or

$$B\mathfrak{g} \simeq \mathfrak{l} B^2 G$$

etc.

$\,$

Its Chevalley-Eilenberg algebra $CE(\mathfrak{B g})$

is called a Sullivan model for $B^2 G$.

$\,$

For example the $L_\infty$-algebra associated with an Eilenberg-MacLane space

$$K(\mathbb{Z},n+1) \simeq B^{n+1}\mathbb{Z}$$

is the line Lie-n algebra from above:

$$\mathfrak{l}(B^{n+1} \mathbb{Z}) \;\simeq\; B^n \mathbb{R} \,.$$

$\,$

The main theorem of rational homotopy theory (Quillen 69, Sullivan 77)

says that the L-∞ algebra $\mathfrak{l}(B^2 G)$ equivalently reflects the rationalization of $B^2 G$

(in fact the real-ification, since we are considering $L_\infty$-algebras over the real numbers).

This means that weak equivalence between $L_\infty$-algebras correspond to maps between spaces

that induce isomorphism on real-ified homotopy groups

$$\left\{ \;\;\;\;\; \array{ B^2 G_1 \overset{\phantom{AA}f\phantom{AA}}{\longrightarrow} B^2 G_2 \\ \text{such that:} \\ \pi_\bullet(B^2 G_1)\otimes_{\mathbb{Z}} \mathbb{R} \underoverset{\simeq}{\pi_\bullet(f) \otimes_{\mathbb{Z}} \mathbb{R} }{\longrightarrow} \pi_\bullet(B^2 G_2) \otimes_{\mathbb{Z}} \mathbb{R} } \;\;\;\;\; \right\} \;\;\;\leftrightarrow\;\;\; \left\{ \; \mathfrak{l}(B^2 G_1) \stackrel{\simeq}{\longrightarrow} \mathfrak{l}(B^2 G_2) \; \right\} \,.$$

For concise review in the language that we use here see Buijs-Félix-Murillo 12, section 2.

$\,$

We apply this rational homotopy theory functor

$$\mathfrak{l}(-) \;\colon\; \text{Spaces} \longrightarrow L_\infty\text{-Algebras}$$

to find the $L_\infty$-algebraic version of parameterized spectra

hence of twisted cohomology:

$\,$

$$\array{ { \text{parameterized} \atop \text{spectrum} } \;\;\;&\;\;\;\; \left\{ \array{ id : B^2 G \to E_n/ B G \to B^2 G \\ E_n/ B G \stackrel{\simeq}{\longrightarrow} \Omega_{B^2 G} (E_{n+1}/ B G) } \right\} \;&\;\leftrightarrow\;&\; \left( \array{ E &\longrightarrow& E/B G \\ && \downarrow \\ && B^2 G } \right) \\ & \mathfrak{l}(-)\downarrow \\ L_\infty\text{Algebra} \;\;\;&\;\;\;\; \left\{ \array{ id : \mathfrak{l}(B^2 G) \to \mathfrak{l}(E_n/ B G) \to \mathfrak{l}(B^2 G) \\ \mathfrak{l}(E_n/ B G) \stackrel{\simeq}{\longrightarrow} \Omega_{\mathfrak{l}(B^2 G)} \mathfrak{l}(E_{n+1}/ B G) } \right\} \;&\;\leftrightarrow\;&\; \left( \array{ V[1] &\longrightarrow& V[1]/\mathfrak{g} \\ && \downarrow \\ && B \mathfrak{g} } \right) }$$

$\,$

Here $V \simeq E \otimes \mathbb{R}$ is a chain complex

underlying the real-ification of the spectrum $E$

(stable Dold-Kan correspondence).

$\,$

So for $\mathbb{R}^{d-1,1\vert \mathbf{N}}$ some super Minkowski spacetime, a cocycle in $\mathfrak{g}$-twisted $V$-cohomology is a diagram of the form

$$\array{ \mathbb{R}^{d-1,1\vert \mathbf{N}} && \overset{}{\longrightarrow} && V/\mathfrak{g} \\ & \searrow && \swarrow \\ && B \mathfrak{g} }$$

$\,$

Now given one stage in the brane bouquet

$$\array{ \widehat{\widehat{\mathfrak{g}}} \\ {}^{\mathllap{hofib(\mu_{p_2})}}\downarrow \\ \hat \mathfrak{g} & \stackrel{\mu_{p_2}}{\longrightarrow} & B\mathfrak{h}_2 \\ {}^{\mathllap{hofib(\mu_{p_1})}}\downarrow \\ \mathfrak{g} &\overset{\mu_{p_1}}{\longrightarrow}& B\mathfrak{h}_1 }$$

we want to descent $\mu_{p_2}$ to $\mathfrak{g}$.

$\,$

By the general theory of principal ∞-bundles (Nikolaus-Schreiber-Stevenson 12):

1. $\widehat{\mathfrak{g}}$ has a $\mathfrak{h}_1$-∞-action

2. equipping $B \mathfrak{h}_2$ with an $\mathfrak{h}_1$-∞-action

   is equivalent to finding a homotopy fiber sequence as on the right here:

   $$\array{ \hat \mathfrak{g} && \stackrel{\mu_2}{\longrightarrow} && \mathbf{B}\mathfrak{h}_2 \\ {}^{\mathllap{hofib(\mu_1)}}\downarrow && && \downarrow^{\mathrlap{hofib(p_\rho)}} \\ \mathfrak{g} && && (\mathbf{B}\mathfrak{h}_2)/\mathfrak{h}_1 \\ & {}_{\mathllap{\mu_1}}\searrow && \swarrow_{\mathrlap{p_\rho}} \\ && \mathbf{B}\mathfrak{h}_1 } \,.$$

3. $\mu_2$ is $\mathfrak{h}_1$-equivariant precisely if it descends to a morphism

   $$\mu_2/\mathfrak{h}_1 \;\colon\; \mathfrak{g} \longrightarrow (\mathbf{B}\mathfrak{h}_2)/\mathfrak{h}_1$$

   such that this diagram commute up to homotopy:

   $$\array{ \hat \mathfrak{g} && \stackrel{\mu_2}{\longrightarrow} && \mathbf{B}\mathfrak{h}_2 \\ {}^{\mathllap{hofib(\mu_1)}}\downarrow && && \downarrow^{\mathrlap{hofib(p_\rho)}} \\ \mathfrak{g} && \stackrel{\mu_2/\mathfrak{h}_1}{\longrightarrow} && (\mathbf{B}\mathfrak{h}_2)/\mathfrak{h}_1 \\ & {}_{\mathllap{\mu_1}}\searrow && \swarrow_{\mathrlap{p_\rho}} \\ && \mathbf{B}\mathfrak{h}_1 } \,.$$

4. if so, then resulting triangle diagram

   $$\array{ \mathfrak{g} && \stackrel{\mu_2/\mathfrak{h}_1}{\longrightarrow} && (\mathbf{B}\mathfrak{h}_2)/\mathfrak{h}_1 \\ & {}_{\mathllap{\mu_1}}\searrow && \swarrow_{\mathrlap{p_\rho}} \\ && \mathbf{B}\mathfrak{h}_1 }$$

   exhibits $\mu_2/\mathfrak{h}_1$ as a cocycle in (rational) $\mu_1$-twisted cohomology

   with respect to the local coefficient bundle $p_\rho$.

$\,$

We now work out this general prescription

for the cocycles in the brane bouquet.

$\,$

RR-fields

$\,$

By the brane bouquet above

the type IIA D-branes

are given by super $L_\infty$ cocycles of the form

$$\mathfrak{string}_{IIA } \overset{\mu_{Dp}}{\longrightarrow} B^{p+1}\mathbb{R}$$

for $p \in \{0,2,4,6,8,10\}$.

$\,$

Notice that

$$H^\bullet(B U, \mathbb{Z})$$

has one generator in each even degree, the universal Chern classes.

Hence the $L_\infty$-algebra

$$\mathfrak{l}(KU)$$

is given by

$$CE(\mathfrak{l}(KU)) \;\simeq\; \left\{ d \omega_{2p+2} = 0 \;\vert\; p \in \mathbb{Z} \right\} \,.$$

This allows to unify the D-brane cocycles

into a single morphism of super $L_\infty$-algebras of the form

$$\array{ \mathfrak{string}_{IIA} && \stackrel{\phantom{AA}\mu_D\phantom{AA}}{\longrightarrow} && \mathfrak{l}(KU) \\ {}^{\mathllap{hofib(\mu_{F1})}}\downarrow \\ \mathbb{R}^{9,1\vert \mathbf{16}+ \overline{\mathbf{16}}} \\ & {}_{\mathllap{\mu_{F1}}}\searrow \\ && \mathbf{B}^2 \mathbb{R} } \,.$$

$\,$

By the above prescription, descending $\mu_D$ is equivalent

to finding a commuting diagram in the homotopy category of super $L_\infty$-algebras

of the form

$$\array{ \mathfrak{string}_{IIA} && \stackrel{\phantom{AA}\mu_D\phantom{AA}}{\longrightarrow} && \mathfrak{l}(KU) \\ {}^{\mathllap{hofib(\mu_{F1})}}\downarrow && && \downarrow^{\mathrlap{hofib(\phi)}} \\ \mathbb{R}^{9,1\vert \mathbf{16}+ \overline{\mathbf{16}}} &&\overset{\phantom{AA}\mu_{D}/B \mathbb{R}\phantom{AA} }{\longrightarrow}&& \text{something} \\ & {}_{\mathllap{\mu_{F1}}}\searrow && \swarrow_{\mathrlap{\phi}} \\ && \mathbf{B}^2 \mathbb{R} } \,.$$

$\,$

This turns out to exist as follows (Fiorenza-Sati-Schreiber 16a, section 5):

Define the $L_\infty$-algebra

$$\mathfrak{l}(KU / BU(1))$$

by

$$CE\left(\mathfrak{l}(KU / BU(1))\right) \;=\; \left\{ \array{ d h_3 = 0\;,\; \\ d \omega_{2p+2} = h_3 \wedge \omega_{2p} } \right\} \,.$$

Moreover write

$$\mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}}_{res}$$

for the super $L_\infty$-algebra whose Chevalley-Eilenberg algebra is

$$CE\left( \mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}}_{res} \right)[f_2,h_3]/(d f_2 = \mu_{F1} + h_3)$$

$\,$

Proposition

(Fiorenza-Sati-Schreiber 16a, theorem 4.16)

The super $L_\infty$-algebra $\mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}}_{res}$

is a resolution of type IIA super-Minkowski spacetime.

in that there is a weak equivalence

$$\mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}}_{res} \stackrel{\phantom{AA}\simeq\phantom{AA}}{\longrightarrow} \mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}} \,.$$

This fits into a commuting diagram of the form

$$\array{ \left\{ {{d e^a = \overline{\psi}\Gamma^a \wedge \psi } \atop {d \psi^\alpha = 0}} \atop { d f_2 = \mu_{F1}} \right\} && \mathfrak{string}_{IIA} && \stackrel{ \mu_D }{\longrightarrow} && \mathfrak{l}(KU) && \left\{ d \omega_{2 p+2} = 0 \right\} \\ && \downarrow^{\mathrlap{hofib(\mu_{F1})}} && && \downarrow^{\mathrlap{\phi}} \\ \left\{ {{d e^a = \overline{\psi}\Gamma^a \wedge \psi } \atop {d \psi^\alpha = 0}} \atop { d f_2 = \mu_{F1} + h_3 } \right\} & & \mathbb{R}_{res}^{9,1\vert \mathbf{16}+ \overline{\mathbf{16}}} && \stackrel{ \mu_{F1/D} }{\longrightarrow} && \mathfrak{l}(KU / B U(1)) && \left\{ d\omega_{2p+2} = h_3\wedge \omega_{2p} \right\} \\ && & {}_{\mathllap{\mu_{F 1}}}\searrow && \swarrow_{\mathrlap{\phi}} \\ && && \mathbf{B}^2 \mathbb{R} \\ && && \left\{ d h_3 = 0 \right\} } \,.$$

$\,$

In conclusion

$\;\;$the type IIA F1-brane and D-brane cocycles with $\mathbb{R}$-coefficients

$\;\;$do descent to super-Minkowski spacetime

$\;\;$as one single cocycle with coefficients

$\;\;$in rationalized twisted K-theory.

$\,$

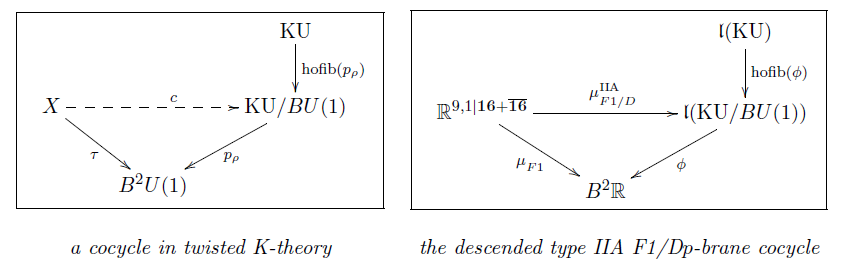
We now say this is more detail:

Consider the type IIA super-Minkowski spacetime $\mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}}$, regarded as its super translation Lie algebra, as discussed above. All of the following has an analogue also for the type IIB super-Minkowski spacetime $\mathbb{R}^{9,1\vert \mathbf{16} + {\mathbf{16}}}$

The 3-cocycle in the old brane scan, as above, which gives the WZW term, of the Green-Schwarz sigma model for the type IIA string (the “F1-brane” in type IIA) is

$$\mu_{F1} \coloneqq \overline{\psi} \Gamma^a \Gamma^{11} \wedge \psi \wedge e_{a} \,.$$

Write

$$\array{ \widehat{\mathbb{R}^{9,1\vert \mathbf{16}+\overline{\mathbf{16}}}} \\ \downarrow \\ \mathbb{R}^{9,1\vert \mathbf{16}+\overline{\mathbf{16}}} \\ & {}_{\mathllap{\mu_{F1}}}\searrow \\ && b^2 \mathbb{R} }$$

for the super Lie 2-algebra extension that the 3-cocycle induces according to def. . By prop. this is given by adjoining an element $f_2$ of degree $(2,even)$ to $CE(\mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}})$ whose CE-differential is the 3-cocycle:

$$CE\left( \widehat{\mathbb{R}^{9,1\vert \mathbf{16}+\overline{\mathbf{16}}}} \right) = \left( CE(\mathbb{R}^{9,1\vert \mathbf{32}+\overline{\mathbf{32}}}) \otimes \langle f_2 \rangle \,, d f_2 = \mu_{F1} \right) \,.$$

Here the homotopy fiber $\widehat{\mathbb{R}^{9,1\vert \mathbf{16}+ \overline{\mathbf{16}}}}$ is the $\mathbf{B}\mathbb{R}$-principal ∞-bundle classified by the 3-cocycle $\mu_{F1}$ for the F1-brane (the type IIA superstring), just like the string Lie 2-algebra-extension of example , but now for the super-part of the symmetry group. Therefore this has sometimes been called the “superstring super Lie 2-algebra”.

Consider then the following inhomogeneous linear combination of elements in the CE-algebra of this super Lie 2-algebra.

Definition

Let $C \in CE(\widehat{\mathbb{R}^{9,1\vert \mathbf{16}+\overline{\mathbf{16}}}})$ be given by

$$\begin{aligned} C \coloneqq \; & \overline{\psi}\Gamma_{10}\wedge\psi \\ & + \tfrac{i}{2} \overline{\psi} \Gamma_{a_1 a_2} \wedge \psi\wedge e^{a_1} \wedge e^{a_2} \\ & + \tfrac{1}{4!} \overline{\psi} \Gamma_{a_1 ... a_4} \Gamma_{10}\wedge \psi \wedge e^{a_1} \wedge \cdots \wedge e^{a_4} \\ & + \tfrac{i}{6!} \overline{\psi} \Gamma_{a_1 ... a_6} \wedge \psi \wedge e^{a_1} \wedge \cdots \wedge e^{a_6} \\ & + \tfrac{1}{8!} \overline{\psi} \Gamma_{a_1 ... a_8} \Gamma_{10} \wedge \psi \wedge e^{a_1} \wedge \cdots \wedge e^{a_8} \\ & + \tfrac{i}{10!} \overline{\psi} \Gamma_{a_1 ... a_{10}} \wedge \psi \wedge e^{a_1} \wedge \cdots \wedge e^{a_{10}} \end{aligned} \,.$$

For $p \in \{0,2,4,6,8, 10\}$ let $\mu_{Dp} \in CE(\widehat{\mathbb{R}^{9,1\vert \mathbf{16}+\overline{\mathbf{16}}}})$ be given by

$$\mu_{Dp} \coloneqq \left[ C \wedge \exp(f_2) \right]_{p+2}$$

where

$$\exp(f) \coloneqq 1 + f_2 + \tfrac{1}{2} f_2 \wedge f_2 + \frac{1}{6} f_2 \wedge f_2 \wedge f_2 + \cdots$$

and where the angular brackets denotes picking the homogeneous summand of degree $p+2$.

Proposition

The elements $\mu_{Dp}$ in def. are non-trivial cocycles.

They are the WZW-terms for the Green-Schwarz sigma-model of the D-branes in type IIA super Minkowski spacetime.

This is due to (Chrysso?malakos-Azcárraga-Izquierdo-Bueno 99, section 6.1). Here we follow the conventions and presentation in (FSS 16a, section 4).

In conclusion, the super Minkowski spacetime $\mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}}$ – locally modeling super spacetimes in 10d type IIA supergravity – carries super $L_\infty$-extensions of the following form (FSS 13):

$$\array{ \widehat{\mathbb{R}^{9,1\vert \mathbf{16}+ \overline{\mathbf{16}}}} && \stackrel{\underset{p=0,2,4,6,8}{\oplus} \mu_{D p}}{\longrightarrow} && \underset{p = 0,2,4,6,8}{\oplus} \mathbf{B}^{p+1}\mathbb{R} \\ \downarrow^{\mathrlap{hofib(\mu_{F1})}} \\ \mathbb{R}^{9,1\vert \mathbf{16}+ \overline{\mathbf{16}}} \\ & {}_{\mathllap{\mu_{F1}}}\searrow \\ && \mathbf{B}^2 \mathbb{R} } \,.$$

By the above (Nikolaus-Schreiber-Stevenson 12), asking whether the cocycles $\mu_{D p}$ for the D-branes are $\mathbf{B}\mathbb{R}$-equivariant and descend as twisted cocycles down to super-Minkowski spacetime is equivalent to asking whether there is a homotopy fiber sequence $\underset{p = 0,2,4,6}{\oplus} \mathbf{B}^{p+1}\mathbb{R} \to something \to \mathbf{B}^2\mathbb{R}$ and a homotopy-commuting diagram of the form

$$\array{ \widehat{\mathbb{R}^{9,1\vert \mathbf{16}+ \overline{\mathbf{16}}}} && \stackrel{\underset{p=0,2,4,6,8}{\oplus} \mu_{D p}}{\longrightarrow} && \underset{p = 0,2,4,6,8}{\oplus} \mathbf{B}^{2p+1}\mathbb{R} \\ \downarrow^{\mathrlap{hofib(\mu_{F1})}} && && \downarrow^{\mathrlap{hofib(\phi)}} \\ \mathbb{R}^{9,1\vert \mathbf{16}+ \overline{\mathbf{16}}} && \stackrel{}{\longrightarrow} && something \\ & {}_{\mathllap{\mu_{F 1}}}\searrow && \swarrow_{\mathrlap{\phi}} \\ && \mathbf{B}^2 \mathbb{R} } \,.$$

To that end, consider the following:

Definition

Write $\left(\underset{p = 0,2,4,6,8}{\oplus}\mathbf{B}^{2p+1}\mathbb{R}\right)/\mathbf{B} \mathbb{R}$ for the L-∞ algebra whose Chevalley-Eilenberg algebra has generators $\omega_2, \omega_4, \omega_6, \omega_8$ and $h_3$ in the indicated degrees, with non-trivial differential given by $d(\omega_{2(k+1)}) = h_3 \wedge \omega_{2k}$:

$$CE \left( \left(\underset{p = 0,2,4,6}{\oplus}\mathbf{B}^{2p+1}\mathbb{R}\right)/\mathbf{B} \mathbb{R} \right) \coloneqq \left\{ \{ \omega_{p+2}, h_3\}_{p = 0,2,4,6}, \; d \omega_{2(k+1)} = h_3 \wedge \omega_{2k} \right\} \,.$$

Example

For $X$ a smooth manifold, then an L-∞ algebra valued differential forms, def. , on $X$ with values in the $L_\infty$-algebra of def.

$$X \longrightarrow \left( \underset{p = 0,2,4,6}{\oplus} \mathbf{B}^{2p+1}\mathbb{R} \right)/\mathbf{B} \mathbb{R}$$

is equivalently a collection of $(2p+2)$-form $G_{2p+2}\in \Omega^{2p+2}(X)$ together with a closed 3-form $H_3 \in \Omega^3(X)_{cl}$ such that

$$d G_{2p+2} = H_3 \wedge G_{2p} \,.$$

For $dim(X) \leq 10$ then this is equivalently a cocycle in the $H_3$-twisted de Rham complex of $X$.

Proposition

The canonical morphisms

$$\array{ && && && \underset{p = 0,2,4,6,8}{\oplus} \mathbf{B}^{2p+1}\mathbb{R} && \left\{ d \omega_{2 k} = 0 \right\} \\ && && && \downarrow \\ && && && \left( \underset{p = 0,2,4,6,8}{\oplus} \mathbf{B}^{2p+1}\mathbb{R} \right)/\mathbf{B} \mathbb{R} && \left\{ d\omega_{2(k+1)} = h_3\wedge \omega_{2k} \right\} \\ && & && \swarrow \\ && && \mathbf{B}^2 \mathbb{R} \\ && && \left\{ d h_3 = 0 \right\} }$$

form a homotopy fiber sequence

Proof

The bottom morphism is clearly degreewise surjective, hence is a fibration between fibrant objects in $sL_\infty Alg$, according to prop. . Therefore according to this proposition its homotopy fiber is equivalent to its ordinary fiber. Dually this is the cofiber in $sdgAlg$ of the map that includes the generator $h_3$, and that is clearly given by sending $h_3$ to zero.

Definition

Write $\mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}}_{res}$ for the super $L_\infty$-algebra whose Chevalley-Eilenberg algebra is that of $\mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}}$ with generators $f_2$ and $h_3$ added, subject to $d_{res} f_2 = \mu_{F1} + h_3$.

Proposition

The super Lie 2-algebra of def. is a resolution of the type IIA super translation Lie algebra, in that the canonical comparison morphism is a weak equivalence according to prop. :

$$\mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}}_{res} \stackrel{\simeq}{\longrightarrow} \mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}}$$

Proof

According to prop. a morphism in $sL_\infty Alg$ is a weak equivalence if it induces a quasi-isomorphism on the co-unary part $d_{CE}^1 \colon \wedge^\bullet \mathfrak{g}^\ast \longrightarrow \wedge^{\bullet + 1}\mathfrak{g}^\ast$ of the Chevalley-Eilenberg algebra. This is manifestly the case by def. of $\mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}}_{res}$.

Hence we may use def. equivalently in place of $\mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}}$. Being a bigger equivalent model of type IIA supertranslations, it potentially serves as domain for more morphisms (it sees more of the derived hom space) in the homotopy theory for super L-infinity algebras in the following.

Indeed, the above descent problem has a solution as follows:

Proposition

The F1/Dp-brane cocycles of type IIA fit into a commuting diagram in $sL_\infty Alg$ of the following form

$$\array{ \left\{ {{d e^a = \overline{\psi}\Gamma^a \wedge \psi } \atop {d \psi^\alpha = 0}} \atop { d f_2 = \mu_{F1}} \right\} && \widehat{ \mathbb{R}^{ 9,1\vert \mathbf{16} + \overline{\mathbf{16}} } } && \stackrel{\underset{p=0,2,4,6,8}{\oplus} \mu_{D p}}{\longrightarrow} && \underset{p = 0,2,4,6,8}{\oplus} \mathbf{B}^{2p+1}\mathbb{R} && \left\{ d \omega_{2 k} = 0 \right\} \\ && \downarrow^{\mathrlap{hofib(\mu_{F1})}} && && \downarrow \\ \left\{ {{d e^a = \overline{\psi}\Gamma^a \wedge \psi } \atop {d \psi^\alpha = 0}} \atop { d f_2 = \mu_{F1} + h_3 } \right\} & & \mathbb{R}_{res}^{9,1\vert \mathbf{16}+ \overline{\mathbf{16}}} && \stackrel{ \left( \omega_{p+2} \mapsto \mu_{D p} \right) }{\longrightarrow} && \left( \underset{p = 0,2,4,6,8}{\oplus} \mathbf{B}^{2p+1}\mathbb{R} \right)/\mathbf{B} \mathbb{R} && \left\{ d\omega_{2(k+1)} = h_3\wedge \omega_{2k} \right\} \\ && & {}_{\mathllap{\mu_{F 1}}}\searrow && \swarrow \\ && && \mathbf{B}^2 \mathbb{R} \\ && && \left\{ d h_3 = 0 \right\} } \,.$$

Here all generators of the same name are undestood to be sent to themselves.

Proof

The key point is that the middle map is indeed a homomorphism. To see this, notice that by def. the resolved differential may be written as

$$d_{res} = d + h_3 \wedge \frac{\partial}{\partial f_2} \,.$$

Applied to def. of the Dp-brane cocycles

$$\mu_{Dp} \coloneqq [C \wedge \exp(f_2)]_{p+2}$$

this yields

$$\begin{aligned} d_{res} \mu_{Dp} & = \underset{= 0}{\underbrace{d \mu_{Dp}}} + h_3 \wedge \frac{\partial}{\partial f_2} [C \wedge \exp(f_2)]_{p+2} \\ & = [C \wedge h_3 \wedge \exp(f_2)]_{p+3} \\ & = h_3 \wedge [C \wedge \exp(f_2)]_{p} \\ & = h_3 \wedge \mu_{D(p-1)} \end{aligned} \,.$$

This equation is exactly what gives a homomrphism into the $L_\infty$-algebra of def. .

This says that the type IIA F1-brane and D-brane cocycles with $\mathbb{R}$-coefficients do descent to super-Minkowski spacetime as one single cocycle with coefficients in the homotopy quotient $\left( \underset{p = 0,2,4,6,8}{\oplus} \mathbf{B}^{2p+1}\mathbb{R} \right)/\mathbf{B} \mathbb{R}$.

But these rational coefficients are precisely the rational image of twisted topological K-theory.

Accordingly, the Lie integration of this rational situation to twisted K-theory, and its globalization over a 10-dimensional IIA super spacetime $X_{10}$, yields a diagram of parameterized spectra in smooth infinity-stacks of the form

$$\array{ X_{10} && \stackrel{RR_{/B}}{\longrightarrow} && KU / \mathbf{B} U(1) \\ & {}_{\mathllap{B}}\searrow && \swarrow \\ && \mathbf{B}^2 U(1) }$$

According to (Sati-Schreiber-Stasheff 09, Nikolaus-Schreiber-Stevenson 12) here the morphism denoted $B$ represents the Kalb-Ramond B-field under which the F1-brane is charged and the morphism denoted $RR_{/B}$ represents the RR-field under which the D-branes are charged.

This is how one may re-discover the familiar cohomological nature of the F1/Dp-brane charges in type II string theory from an analysis of the super $L_\infty$-cohomology embodied in the brane bouquet-refinement of the old brane scan.

M-flux fields

$\,$

The part of the brane bouquet giving the M-branes is

$$\array{ \mathfrak{m}2\mathfrak{brane} &\stackrel{\mu_{M5}}{\longrightarrow}& \mathbf{B}^6 \mathbb{R} \\ {}^{\mathllap{hofib(\mu_{M2})}}\downarrow \\ \mathbb{R}^{10,1\vert \mathbf{32}} & \stackrel{\mu_{M2}}{\longrightarrow} & \mathbf{B}^3 \mathbb{R} \\ {}^{\mathllap{hofib(\mu_{D 0})}}\downarrow \\ \mathbb{R}^{9,1\vert \mathbf{16} + \overline{\mathbf{16}}} }$$

$\,$

In order to descend this, consider the $L_\infty$-algebra corresponding to the 4-sphere

$$\mathfrak{l}(S^4) \,.$$

By standard results on rational n-spheres, this is given by

$$CE(\mathfrak{l}S^4) \;\simeq\; \left\{ \array{ d \, g_4 = 0\,,\, \\ d\, g_7 + \tfrac{1}{2} g_4 \wedge _4 = 0 } \right\} \,.$$

Proposition

Fiorenza-Sati-Schreiber 15, section 3

There is a homotopy fiber sequence of $L_\infty$-algebras as on the right

$$\left( \array{ && S^7 \\ && \downarrow \\ && S^4 \\ & \swarrow \\ B SU(2) \\ \downarrow^{\mathrlap{c_2}} \\ B^3 U(1) } \right) \;\; \stackrel{\phantom{AA}\mathfrak{l}(-)\phantom{AA} }{\mapsto} \;\; \left( \array{ && B^6 \mathbb{R} \\ && \downarrow^{\mathrlap{ hofib(\mathfrak{l}(c_2)) } } \\ &&\mathfrak{l}(S^4) \\ & \swarrow_{\mathfrak{l}(c_2)} \\ B^3 \mathbb{R} } \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \right)$$

which is the image under $\mathfrak{l}(-)$ of the quaternionic Hopf fibration.

This makes a commuting diagram

in the homotopy category of super $L_\infty$-algebas

of the form

$$\array{ \left\{ { { d e^a = \overline{\psi}\wedge \Gamma^a \wedge \psi } \atop { d \psi^\alpha = 0 } } \atop d h_3 = - \mu_{M2} \right\} && \mathfrak{m}2\mathfrak{brane} && \stackrel{ \mu_{M5} }{\longrightarrow} && B^6 \mathbb{R} && \left\{ d g_7 = 0 \right\} \\ && \downarrow^{\mathrlap{hofib(\mu_{M2})}} && && \downarrow^{\mathrlap{hofib(\mathfrak{l}(c_2))}} \\ \left\{ { { d e^a = \overline{\psi}\wedge \Gamma^a \wedge \psi } \atop { d \psi^\alpha = 0 } } \atop d h_3 = g_4 - \mu_{M2} \right\} && \mathbb{R}_{res}^{10,1\vert\mathbf{32}} && \stackrel{ \mu_{M2/M5} }{\longrightarrow} && \mathfrak{l} S^4 && \left\{ {d g_4 = 0} \atop {d g_7 + \tfrac{1}{2} g_4 \wedge g_4 = 0} \right\} \\ && & {}_{\mathllap{\mu_{M2}}}\searrow && \swarrow_{\mathrlap{\mathfrak{l}(c_2)}} \\ && && \mathbf{B}^3 \mathbb{R} \\ && && \left\{ d g_4 = 0\right\} }$$

In conclusion

$\;\;$this says that, rationally,

$\;\;$M2-brane charge is in degree-4 ordinary cohomology

$\;\;$and it twists M5-brane charge

$\;\;$which is, rationally, in unstable degree-4 cohomotopy.

$\,$

This confirms a conjecture due to

(Sati 10, section 6.3, Sati 13, section 2.5).

based on the observation that

the equations of motion of 11-dimensional supergravity

for the supergravity C-field field strength $G_4$ say that

$$d G_7 + \tfrac{1}{2} G_4 \wedge G_4 = 0$$

with $G_7 = \ast G_4$ the Hodge dual

and this is just the algebraic relation for the Sullivan model of the rational 4-sphere.

$\,$

Notice that, unstably, the 4-sphere

is just the space whose non-torsion homotopy groups

hence those that are visible in rational homotopy theory

are in degrees 2+2 and 5+2:

k	1	2	3	4	5	6	7
$\phantom{AA}\pi_k(S^4)\phantom{AA}$	$\phantom{AA}0\phantom{AA}$	$\phantom{AA}0\phantom{AA}$	$\phantom{AA}0\phantom{AA}$	$\phantom{AA}\mathbb{Z}\phantom{AA}$	$\phantom{AA}\mathbb{Z}/2\phantom{AA}$	$\phantom{AA}\mathbb{Z}/2\phantom{AA}$	$\phantom{AA}\mathbb{Z} \oplus \mathbb{Z}/{12}\phantom{AA}$

$\,$

But the correct non-rational lift of the $\mathfrak{l}(S^4)$-coefficients

will also have to be such that it somehow gives rise to twisted K-theory

under (double) dimensional reduction. This is still an open problem.

For further comments see the talk

Equivariant cohomology of M2/M5-branes

$\,$

Now we say this in more detail:

We focus now on the cocycle in the brane bouquet that gives the WZW term of the Green-Schwarz sigma model for the M5-brane, defined on the extended super Minkowski spacetime induced from the cocycle for the M2-brane. Then we show how it descends down to 11-dimensional super-Minkowski spacetime itself, unifying with the M2-cocycle to one single cocycle, but now with coefficient in the rational 4-sphere.

Definition

For $p \in \mathbb{N}_{even}$, write $b^{2p+2} \mathbb{R}/b^p \mathbb{R}$ for the L-∞ algebra given by the Chevalley-Eilenberg algebra

$$CE(b^{2p+2} \mathbb{R}/b^p \mathbb{R}) = \left(\left\langle g_{p+2}, g_{2p+3}\right\rangle), {{d g_{p+2} = 0} \atop {d g_{2p+3} = g_{p+2} \wedge g_{p+2}}}\right) \,.$$

Remark

Regarded as a Sullivan model in rational homotopy theory, then the dg-algebra of def. is a minimal model for the rationalization of the $(p+2)$-sphere.

By the recognition theorem for L-∞ extensions we get:

Proposition

For $p \in \mathbb{N}_{even}$, there is a homotopy fiber sequence in the homotopy theory of L-∞ algebras of the form

$$\array{ b^{2p+2} \mathbb{R} \\ \downarrow \\ b^{2p+2} \mathbb{R}/b^{p}\mathbb{R} &\stackrel{}{\longrightarrow}& b^{p+1}\mathbb{R} }$$

where on formal dual Chevalley-Eilenberg algebras in terms of our defining generating elements the horizontal map is given by $g_{p+4}\mapsto g_{p+4}$ and the vertical map by $g_{p+4}\mapsto 0$ and $g_{2p+3}\mapsto g_{2p+3}$.

By the discussion at ∞-action this exhibits a $b^{p}\mathbb{R}$-action on $b^{2p+2}\mathbb{R}$, for which $b^{2p+2} \mathbb{R}/b^{p}\mathbb{R}$ is the homotopy quotient, whence the notation.

Example

For $p=2$ and regarded as a statement in rational homotopy theory via remark , then the extension in prop. is a Sullivan minimal model for the rationalized Hopf fibration

$$\array{ S^3 &\longrightarrow& S^7 \\ && \downarrow \\ && S^4 }$$

Proposition

The elements $\mu_4, \mu_7 \in CE(\mathbb{R}^{10,1\vert \mathbf{32}})$, def. , satisfy

1. $d \mu_4 = 0$;

2. $d \mu_7 = 15 \, \mu_4 \wedge \mu_4$

Prop. is originally due to (D’Auria-Fré 82, p.18), where it is considered as an ingredient for constructing the action functional of 11-dimensional supergravity in the D'Auria-Fré formulation of supergravity. The statement has been rediscovered in (BLNPST 97, (9)), finding its interpretation as giving the WZW term of the Green-Schwarz sigma model for the M5-brane.

Definition

Write $\mathfrak{m}2\mathfrak{brane} \in sL_\infty Alg$ for the super L-∞ algebra which is the homotopy fiber of $\mu_4$ in prop. .

$$\array{ \mathfrak{m}2\mathfrak{brane} \\ \downarrow \\ \mathbb{R}^{10,1\vert \mathbf{32}} &\stackrel{\mu_4}{\longrightarrow}& b^3 \mathbb{R} } \,.$$

and specifically for the representive of this homotopy fiber which, by the recognition theorem for L-∞ extensions, is given by having the Chevalley-Eilenberg algebra

$$CE(\mathfrak{m}2\mathfrak{brane}) = (CE(\mathbb{R}^{10,1\vert \mathbf{32}})\otimes \langle c_3\rangle, d c_3 = -\mu_4) \,.$$

In terms of def. , the second item in prop. reads as follows:

Corollary

There is a super $L_\infty$-cocycle of the form

$$\mathfrak{m}2\mathfrak{brane} \stackrel{c_3 \wedge \mu_4 + \frac{1}{15} \mu_7}{\longrightarrow} b^6 \mathbb{R} \,.$$

But since $\mathfrak{m}2\mathfrak{brane}$ is a $b^2 \mathbb{R}$-principal ∞-bundle, it is natural to ask whether $c_3 \wedge \mu_4 + \frac{1}{15} \mu_7$ is $b^2 \mathbb{R}$-equivariant with respect to some natural $b^2\mathbb{R}$-∞-action on $b^6 \mathbb{R}$. Such a natural action is given by prop. . To exhibit in components the equivariance of the 7-cocycle in corollary with respect to this action we need a resolution of super Minkowski spacetime:

Definition

Write $\mathbb{R}_{res}^{10,1\vert \mathbf{32}}$ for the super L-∞ algebra whose Chevalley-Eilenberg algebra is obtained from that of super Minkowski spacetime by

$$CE\left( \mathbb{R}_{res}^{10,1\vert \mathbf{32}} \right) \coloneqq \left( CE\left( \mathbb{R}^{10,1\vert \mathbf{32}}\right)\otimes \left\langle h_3, g_4\right\rangle , {{d h_3 = g_4 - \mu_4} \atop {d g_4 = 0}} \right) \,.$$

Proposition

The canonical morphism

$$\mathbb{R}_{res}^{10,1\vert \mathbf{32}} \stackrel{\simeq}{\longrightarrow} \mathbb{R}^{10,1\vert \mathbf{32}}$$

given dually by $\psi^\alpha \mapsto \psi^\alpha$, $e^a \mapsto e^a$, is an equivalence of $L_\infty$-algebras. It factors the morphism $\mathfrak{m}2\mathfrak{brane} \longrightarrow \mathbb{R}^{10,1\vert \mathbf{32}}$ from def. through a morphism $\mathfrak{m}2\mathfrak{brane} \longrightarrow \mathbb{R}^{10,1\vert \mathbf{32}}_{res}$ which on formal dual CE-elements is given by $h_3 \mapsto 0$, $g_4 \mapsto 0$ and by being the identity on all other generators.

Proposition

There is a diagram of L-∞ algebras of the form

$$\array{ && \vdots && && \vdots \\ && \downarrow \downarrow && && \downarrow \downarrow \\ && \mathfrak{m}2\mathfrak{brane} && \stackrel{h_3 \wedge \mu_4 + \frac{1}{15}\mu_7 }{\longrightarrow} && b^6 \mathbb{R} \\ && \downarrow && && \downarrow \\ \mathbb{R}^{10,1\vert\mathbf{32}} &\stackrel{\simeq}{\longleftarrow}& \mathbb{R}_{res}^{10,1\vert\mathbf{32}} && \stackrel{h_3 \wedge (g_4 + \mu_4) + \frac{1}{15}\mu_7 }{\longrightarrow} && b^6 \mathbb{R}/b^2 \mathbb{R} \\ && & {}_{\mathllap{}}\searrow && \swarrow \\ && && b^3 \mathbb{R} }$$

Proof

That the diagram exists and commutes at the level of the underlying graded algebras of the formal dual CE-algebras is immediate in terms of the defining generators: each generator is mapped to the generator of the same name, if present, in the codomain, or to zero otherwise, except for $g_7 \in CE(b^6 \mathbb{R})$ which is sent to $h_3 \wedge \mu_4 + \frac{1}{15}\mu_7$ and $g_7 \in CE(b^6 \mathbb{R}/b^2 \mathbb{R})$, which is sent to $h_3 \wedge (g_4 + \mu_4) + \frac{1}{15}\mu_7$, as indicated.

It remains to check that the middle horizontal map respects the CE-differentials: by prop. we have

$$\begin{aligned} d(h_3 \wedge (g_4 + \mu_4) + \frac{1}{15}\mu_7) &= (g_4 - \mu_4) \wedge (g_4 + \mu_4) + \mu_4 \wedge \mu_4 \\ & = g_4 \wedge g_4 \end{aligned}$$

and by def. this says indeed that $g_7 \mapsto h_3 \wedge (g_4 + \mu_4) + \frac{1}{15}\mu_7$ respects the CE-differentials.

Remark

The form of the equivariant cocycle in prop. is that of the curvature of the WZW term of the sigma-model describing the M5-brane as considered in (BLNPST 97, (6),(8)).

Remark

In view of remark , prop. says that the CE-elements $\mu_4$ and $\mu_7$ of prop. define a cocycle with values in the rational 4-sphere. In the discussions in geometry of physics – WZW terms and geometry of physics – BPS charges we see that under Lie integration and globalization in higher Cartan geometry, these elements encode the supergravity C-field and its magnetic dual. That these fields should take values the 4-sphere was first suggested in (Sati 13, section 2.5). See (Fiorenza-Sati-Schreiber 15) for more.

Dimensional reduction

Now that we have found

the descended $L_\infty$-cocycles

for all super $p$-branes

in twisted cohomology, rationally,

we may analyze their behaviour under double dimensional reduction

and discover the super $L_\infty$-algebraic incarnation

of various dualities in string theory.

Definition

For $\mathfrak{g}$ any super L-∞ algebra of finite type, its cyclification

$$\mathfrak{L}\mathfrak{g}/\mathbb{R} \in s L_\infty Alg_{\mathbb{R}}$$

is defined by having Chevalley-Eilenberg algebra of the form

$$CE(\mathfrak{L}\mathfrak{g}/\mathbb{R}) \coloneqq \left( \wedge^\bullet \left( \underset{\text{original}}{\underbrace{\mathfrak{g}^\ast}} \oplus \underset{\text{shifted copy}}{\underbrace{s\mathfrak{g}^\ast}} \oplus \underset{\text{new generator} \atop \text{in degree 2}}{\underbrace{\langle \omega_2 \rangle}} \right) \;,\; d_{\mathfrak{d}\mathfrak{g}/\mathbb{R}} \;\colon\; \left\{ \array{ \omega_2 &\mapsto& 0 \\ \alpha &\mapsto& d_{\mathfrak{g}} \alpha + \omega_2 \wedge s \alpha \\ s \alpha &\mapsto& - s d_{\mathfrak{g}} \alpha } \right. \right)$$

where

$$s \mathfrak{g}^\ast$$

is a copy of $\mathfrak{g}^\ast$ with cohomological degrees shifted down by one, and where $\omega$ is a new generator in degree 2.

The differential is given for $\alpha \in \wedge^1 \mathfrak{g}^\ast$ by

$$d_{\mathfrak{d}\mathfrak{g}/\mathbb{R}} \;\colon\; \left\{ \array{ \omega_2 &\mapsto& 0 \\ \alpha &\mapsto& d_{\mathfrak{g}} \alpha \pm \omega_2 \wedge s \alpha \\ s \alpha &\mapsto& - s d_{\mathfrak{g}} \alpha } \right.$$

where on the right we are extendng $s$ as a graded derivation.

Define

$$\mathfrak{L}\mathfrak{g} \in s L_\infty Alg_{\mathbb{R}}$$

in the same way, but with $\omega_2 \coloneqq 0$.

For every $\mathfrak{g}$ there is a homotopy fiber sequence

$$\array{ && \mathfrak{L}\mathfrak{g} \\ && \downarrow \\ && \mathfrak{L} \mathfrak{g}/\mathbb{R} \\ & \swarrow_{\mathrlap{\omega_2}} \\ B \mathbb{R} }$$

which hence exhibits $\mathfrak{L} \mathfrak{g}/\mathbb{R}$ as the homotopy quotient of $\mathfrak{L}\mathfrak{g}$ by an $\mathbb{R}$-action.

Proposition

(Vigué-Sullivan 76, Vigué-Burghelea 85)

If

$$\mathfrak{g} = \mathfrak{l}(X)$$

is the $L_\infty$-algebra associated by rational homotopy theory to a simply connected topological space $X$, then

$$\mathfrak{L}( \mathfrak{l}(X) ) \simeq \mathfrak{l}( \mathcal{L}X )$$

corresponds to the free loop space of $X$ and

$$\mathfrak{L}( \;\mathfrak{l}( X )\; )/\mathbb{R} \simeq \mathfrak{l}( \;\mathcal{L}X/S^1\; )$$

corresponds to the homotopy quotient of the free loop space by the circle group action which rotates the loops.

The cochain cohomology of the Chevalley-Eilenberg algebra

$$CE(\mathfrak{l}( \;\mathcal{L}X/S^1\; ))$$

computes the cyclic cohomology of $X$ with coefficients in $\mathbb{R}$.

(Whence “cyclification”.)

Moreover the homotopy fiber sequence of the cyclification corresponds to that of the free loop space:

$$\left( \array{ \mathcal{L}X \\ \downarrow^{\mathrlap{hofib(p)}} \\ \mathcal{L}X/S^1 \\ \downarrow^{\mathrlap{p}} \\ B S^1 } \;\;\;\;\;\;\;\; \right) \;\;\;\; \stackrel{\phantom{AA}\mathfrak{l}(-)\phantom{AA}}{\mapsto} \;\;\;\; \left( \array{ \mathfrak{L} \mathfrak{l}(X) \\ \downarrow^{ \mathrlap{ hofib( \mathfrak{l}(p) ) } } \\ \mathfrak{L}\mathfrak{l}(X)/\mathbb{R} \\ \downarrow^{\mathrlap{\mathfrak{l}(p)}} \\ B \mathbb{R} } \;\;\;\;\;\;\;\; \right)$$

$\,$

The following gives an $L_\infty$-theoretic formalization

of “double dimensional reduction”

by which both the spacetime dimension is reduced

while at the same time the brane dimension

reduces (if wrapping the reduced dimension).

$\,$

Proposition

(Fiorenza-Sati-Schreiber 16b, prop. 3.5)

For

$$\array{ \widehat{\mathfrak{g}} \\ \downarrow \\ \mathfrak{g} \\ & {}_{\mathllap{\mu_2}}\searrow \\ && B \mathbb{R} }$$

a central extension of super Lie-∞ algebras, then the operation

of sending a super $L_\infty$-homomorphsm of the form

$$\widehat{\mathfrak{g}} \overset{\phi}{\longrightarrow} \mathfrak{h}$$

to the composite

$$\mathfrak{g} \longrightarrow \mathfrak{L}\widehat{\mathfrak{g}}/\mathbb{R} \overset{\mathfrak{L}\phi/\mathbb{R}}{\longrightarrow} \mathfrak{L}\mathfrak{h}/\mathbb{R}$$

gives a natural bijection

$$\array{ Hom( \widehat{\mathfrak{g}}, \mathfrak{h} ) \;&\; \underoverset {\underset{oxidation}{\longleftarrow}} {\overset{reduction}{\longrightarrow}} {\simeq} \;&\; Hom_{/B\mathbb{R}}( \mathfrak{g}, \mathfrak{L}\mathfrak{h}/\mathbb{R} ) \\ \\ \left( \array{ \widehat{\mathfrak{g}} \overset{}{\longrightarrow} \mathfrak{h} } \right) \;&\; \leftrightarrow \;&\; \left( \array{ \mathfrak{g} && \overset{}{\longrightarrow} && \mathfrak{L}\mathfrak{h}/\mathbb{R} \\ & {}_{\mathllap{\mu_2}}\searrow && \swarrow_{\mathrlap{\omega_2}} \\ && B \mathbb{R} } \right) }$$

between super $L_\infty$-homomorphisms out of the exteded super $L_\infty$-algebra $\widehat{\mathfrak{g}}$

and homomorphism out of the base $\mathfrak{g}$ into the cyclification of the original coefficients

with the latter constrained so that

the canonical 2-cocycle on the cyclification is taken to the 2-cocycle classifying the given extension.

It is straightforward, if somewhat tedious, to check this explicitly.

Remark

The general theory of adjoint functors provides insight as to the geometric nature of the super $L_\infty$-algebraic formalization of dimensional reduction from prop. . Namely given any pair of adjoint functors $L \dashv R$, then there is a canonical natural morphism $\eta_x : x \to R L x$ (called the unit of the adjunction) such that the natural bijection between hom-sets

$$\mathrm{Hom}(L x, y) \overset{\simeq}{\longrightarrow} \mathrm{Hom}(x,R x)$$

is given by sending any morphism of the form $\phi : L x \to y$ to the composite

$$x \overset{\eta_x}{\longrightarrow} R L x \overset{R \phi}{\longrightarrow} R y \,.$$

Specified to the situation in Prop. , this means that the double dimensional reduction of a super $L_\infty$-homomorphism

$$\widehat{\mathfrak{g}} \overset{\phi}{\longrightarrow} \mathfrak{h}$$

on a central $\mathbb{R}$-extension $\widehat{\mathfrak{g}}$ of some super $L_\infty$-algebra $\mathfrak{g}$ is the following composite:

$$\mathfrak{g} \overset{\eta_{\mathfrak{g}}}{\longrightarrow} \mathfrak{L} \widehat{\mathfrak{g}} / \mathbb{R} \overset{\mathfrak{L}(\phi)/\mathbb{R}}{\longrightarrow} \mathfrak{L}\mathfrak{h}/\mathbb{R} \,.$$

In terms of the geometric interpretation via rational homotopy theory from prop. the morphism $\eta_{\mathfrak{g}}$ here has the following interpretation:

Let $\widehat X \to X$ be a principal circle bundle. Then there is a map

$$X \longrightarrow \mathcal{L}\widehat X/ S^1$$

which sends each point of $X$ to the loop that winds around the circle fiber over that point, at unit speed. As a map to the free loop space $\mathcal{L}\widehat{X}$ this would not be well defined unless the circle bundle were trivial, because by definition of principal circle bundles its fibers are identified with the typical fiber (the circle) only up to rigid rotation of that circle. But this is precisely the relation that is divided out by passing to the cyclified space $\mathfrak{L}\widehat{X}/S^1$, which makes the above well defined.

Hence given any map of spaces $\widehat{X} \overset{f}{\longrightarrow} H$ we may pass to the induced map on loops in $\widehat{X}$ modulo rigid rotation, and then precompose with the above fiber-assigning map

$$X \longrightarrow \mathcal{L}\widehat{X}/S^1 \overset{\mathcal{L}f/S^1}{\longrightarrow} \mathcal{L}H/S^1 \,.$$

Under the Quillen-Sullivan functor from spaces to their associated $L_\infty$-algebras in rational homotopy theory, this is the $L_\infty$-algebraic construction above.

And this shows just how this formalizes the intuitive picture of dimensional reduction. For let $\Sigma_{p+1}$ be a manifold of dimension $p+1$ and let $\Sigma_{p+1} \longrightarrow X$ be the worldvolume of some $p$-brane in $X$. Thinking of $f : \widehat{X} \to H$ as classifying a background field for $(p+1)$-branes on $\widehat{X}$ (for instance for $H = K(\mathbb{Z},p+3)$, the classifying space for ordinary cohomology) then the dimensionally reduced coupling term is given by the composite

$$\Sigma_{p+1} \longrightarrow X \longrightarrow \mathcal{L}\widehat{X}/S^1 \overset{\mathcal{L}f/S^1}{\longrightarrow} \mathcal{L}H/S^1 \,.$$

To see what this does, consider what happens locally over some chart $U$ on which the circle extension $\widehat{X} \to X$ is topologically trivial. Then by the adjunction $S^1 \times (-) \dashv [S^1,-] = \mathcal{L}(-)$ this is equivalently the composite

$$\Sigma_{p+1} \times S^1 \longrightarrow \widehat U \overset{f|_U}{\longrightarrow} H \,.$$

But this is nothing than the value of the background field $f$ not on the $p$-brane worldvolume $\Sigma_{p+1}$, but on the worldvolume $\Sigma_{p+1} \times S^1$ of a $(p+1)$-brane, which “wraps” the circle fiber in $\widehat U = U \times S^1$. This is the physical picture of double dimensional reduction.

For entertainment of the homotopy theory cognoscenti, I mention that this formalization of double dimensional reduction from prop. is but a special case of the following very general fact in (∞,1)-topos theory.

Proposition

Let $G$ be an ∞-group in an (∞,1)-topos $\mathbf{H}$ then there is a pair of adjoint ∞-functors of the form

$$\mathbf{H} \underoverset {\underset{[G,-]/G}{\longrightarrow}} {\overset{hofib}{\longleftarrow}} {\bot} \mathbf{H}_{/\mathbf{B}G} \,,$$

where $[G,-]]$ denotes the internal hom in $\mathbf{H}$, $[G,-]/G$ denotes the homotopy quotient by the conjugation ∞-action for $G$ equipped with its canonical ∞-action by left multiplication and the argument regarded as equipped with its trivial $G$-$\infty$-action.

Proof

First observe that the conjugation action on $[G,X]$ is the internal hom in the (∞,1)-category of $G$-∞-actions $Act_G(\mathbf{H})$. Under the equivalence of (∞,1)-categories

$$Act_G(\mathbf{H}) \simeq \mathbf{H}_{/\mathbf{B}G}$$

(from Nikolaus-Schreiber-Stevenson 12) then $G$ with its canonical ∞-action is $(\ast \to \mathbf{B}G)$ and $X$ with the trivial action is $(X \times \mathbf{B}G \to \mathbf{B}G)$.

Hence

$$[G,X]/G \simeq [\ast, X \times \mathbf{B}G]_{\mathbf{B}G} \;\;\;\;\; \in \mathbf{H}_{/\mathbf{B}G} \,.$$

Actually, this is the very definition of what $[G,X]/G \in \mathbf{H}_{/\mathbf{B}G}$ is to mean in the first place, abstractly.

But now since the slice (∞,1)-topos $\mathbf{H}_{/\mathbf{B}G}$ is itself cartesian closed, via

$$E \times_{\mathbf{B}G}(-) \;\;\; \dashv \;\;\; [E,-]_{\mathbf{B}G}$$

it is immediate that there is the following sequence of natural equivalences

$$\begin{aligned} \mathbf{H}_{/\mathbf{B}G}(Y, [G,X]/G) & \simeq \mathbf{H}_{/\mathbf{B}G}(Y, [\ast, X \times \mathbf{B}G]_{\mathbf{B}G}) \\ & \simeq \mathbf{H}_{/\mathbf{B}G}( Y \times_{\mathbf{B}G} \ast, \underset{p^\ast X}{\underbrace{X \times \mathbf{B}G }} ) \\ & \simeq \mathbf{H}( \underset{hofib(Y)}{\underbrace{p_!(Y \times_{\mathbf{B}G} \ast)}}, X ) \\ & \simeq \mathbf{H}(hofib(Y),X) \end{aligned}$$

Here $p \colon \mathbf{B}G \to \ast$ denotes the terminal morphism and $p_! \dashv p^\ast$ denotes the base change along it.

$\,$

Dualities

$\,$

We discuss now how

by repeatedly applying

the super $L_\infty$-algebraic dimensional reduction/oxidation isomorphism of prop.

to the descended cocycles from the brane bouquet

yields super $L_\infty$-algebraic equivalences

that reflect the pertinent dualities in string theory

1. between M-theory and type IIA string theory;

2. between type IIA string theory and type IIB string theory (T-duality)

3. between type IIB string theory and F-theory.

$\,$

M/IIA

Proposition

(Fiorenza-Sati-Schreiber 16a, section 3)

The cyclification of the M-brane coefficient $\mathfrak{l}(S^4)$

is the truncated IIA F1/D-brane coefficient $\mathfrak{l}( KU\langle 0,6 \rangle ( B U(1) )$

with an extra twist for the NS5-brane:

$$CE\left( \mathfrak{L} S^4 / \mathbb{R} \right) \;\simeq\; CE\left(\, \underset{\text{F1/Dp-branes}}{\underbrace{ \mathfrak{l}(KU\langle 0,6\rangle/B U(1)) }} \, \right) \underset{\text{NS5-brane}}{\underbrace{ [h_7]/(d h_7 = \omega_2 \wedge \omega_6 - \omega_4 \wedge \omega_4) }} \,.$$

Under this identification

the $L_\infty$-theoretic dimensional reduction according to prop.

of the unified M-brane cocycle $\mu_{M2/M5}$ of prop.

along the M-theory extension from example

is the unified type IIA F1/D-brane cocycle from prop. :

$$\array{ 11d, N = 1 && \mathbb{R}^{10,1\vert \mathbf{32}} &\overset{\mu_{M2/M5}}{\longrightarrow}& \mathfrak{l}(S^4) \\ && \downarrow \\ 10d, \text{type IIA} && \mathbb{R}^{9,1\vert \mathbf{16}+ \overline{\mathbf{16}}} &\overset{ \mathfrak{L}(\mu_{M2/M5})/\mathbb{R} }{\longrightarrow}& \mathfrak{l}(\mathcal{L}S^4/S^1) \\ && & {}_{\mathllap{\mu^{A}_{F1/D{\leq 4}}}}\searrow & \downarrow \\ && && \mathfrak{l}( KU\langle 0,6\rangle/B U(1) ) }$$

IIA/IIB

(…)

FSS16b, sections 5 and 6

(…)

IIB/F

(…)

FSS16b, section 7

(…)

Session III

We had seen in session I how infinitesimal symmetries of higher WZW terms over smooth manifolds form extensions of symmetry algebras by de Rham cohomology groups; and in session II we had seen that in general higher WZW terms are defined consecutively on higher group stack extensions defined by previous WZW terms. Here we consider now the full finite symmetries of such consecutive higher WZW terms, not just infinitesimally at the $L_\infty$-algebra level.

To make progress here, it is useful not to work in componentwise presentations such as given by simplicial presheaves, but to consider the situation more general abstractly. The general abstract context of higher stacks is captured by the statement that the collection of all of them (over a given site, for us here a site of smooth manifolds or supermanifolds or similar) forms what is called an (∞,1)-topos. In this last session we will need to speak more internally to such higher toposes.

We write generically $\mathbf{H}$ for an (∞,1)-topos. The case of relevance for the examples discussed here is the $\infty$-topos of higher smooth stacks, higher superstacks, and we will now also need higher formal stacks containing infinitesimals. $\mathbf{H} =$super formal smooth higher stacks.

Homotopy stabilizer groups

Given a Deligne cocycle $\mathbf{L}^X \colon X \longrightarrow \mathbf{B}^{p+1}(\mathbb{R}/\Gamma)_{conn}$ on some higher smooth stack $X$, we want to study its symmetries, namely the automorphisms (diffeomorphisms) $\phi \colon X \stackrel{\simeq}{\to} X$ that preserve $\mathbf{L}^X$. Since we are in a higher homotopy theoretic context, “preserving” here means to choose an equivalence $\eta \colon \phi^\ast \mathbf{L}^X \stackrel{\simeq}{\longrightarrow} \mathbf{L}^X$, and these choices of equivalences in turn have higher order equivalences between themselves, and so on.

Definition

Given an (∞,1)-topos $\mathbf{H}$, then a group object in $\mathbf{H}$ (an ∞-group) is an object $G \in \mathbf{H}$ equipped with the structure of an A-∞ algebra (i.e. a product operation which satisfies associativity up to higher coherent homotopy), such that the 0-truncation $\tau_0 G$ is an ordinary group object.

Example

Given any object $X$ with a base point $x \colon \ast \to X$ (a pointed object), then the loop space object $\Omega_x X$, defined to be the homotopy fiber product of the point over $X$ with itself, canonically has the structure of an ∞-group, def. , where the product operation is given by concatenation of loops.

Compared to the somewhat intricate structure of an A-∞ algebra (grouplike or not), the concept of a pointed object is drastically more simple and more fundamental. It becomes simpler still if we assume that up to equivalence $X$ only has a single map from the point, then we call $X$ a connected object.

Proposition

The looping operation of example constitutes an equivalence of (∞,1)-categories

$$Grp(\mathbf{H}) \stackrel{\overset{\Omega}{\longleftarrow}}{\underoverset{\mathbf{B}}{\simeq}{\longrightarrow}} \mathbf{H}_{\geq 1}^{\ast /}$$

between pointed connected objects in $\mathbf{H}$ and ∞-group objects, def. , in $\mathbf{H}$.

The inverse equivalence $\mathbf{B}$ we call the delooping operation.

For $\mathbf{H} =$ ∞Grpd this is the May recognition theorem. For general $\mathbf{H}$ this is (Lurie, "Higher Algebra", theorem 5.1.3.6).

Various concepts in group theory and representation theory become elementary under passing along $\mathbf{B}$ in this equivalence. The following is particularly useful:

Proposition

Given an ∞-group $G$, then there is an equivalence of (∞,1)-categories

$$G Act(\mathbf{H}) \stackrel{\simeq}{\longrightarrow} \mathbf{H}_{/\mathbf{B}G}$$

between ∞-actions of $G$ on objects $V \in \mathbf{H}$ and objects in the slice (∞,1)-topos over $\mathbf{B}G$, given by identifying a $G$-∞-action $\rho$ on some $V$ with the homotopy fiber sequence

$$\array{ V &\stackrel{i}{\longrightarrow}& V/G \\ && \downarrow^{\mathrlap{p_\rho}} \\ && \mathbf{B}G }$$

where $V/G$ is the homotopy quotient (the homotopy coinvariants) of the action.

In traditional plain homotopy theory this is due to (Dror-Dwyer-Kan 80). For general (∞,1)-toposes this is discussed in (Nikolaus-Schreiber-Stevenson 12).

One immediate consequence of this equivalence is that it implies that $G Act(\mathbf{H})$ is itself an (∞,1)-topos and in particular has internal homs:

Example

For $(V_1,\rho_1)$ and $(V_2,\rho_2)$ two $G$-actions, then there is the conjugation action

$$\array{ [V_1,V_2] &\longrightarrow& [V_1,V_2]/_{conj}G \\ && \downarrow^{\mathrlap{p_{conj}}} \\ && \mathbf{B}G } \,,$$

where

$$[V_1,V_2]/_{conj}G \coloneqq [\rho_1,\rho_2]$$

is the internal hom of the two actions formed in the slice over $\mathbf{B}G$.

Another consequence is that the object classifier in an (∞,1)-topos/universe $Type \in \mathbf{H}$ yields the canonical automorphism actions:

Example

For $V \in \mathbf{H}$ any object, then its delooped automorphism ∞-group is the 1-image $\mathbf{B}\mathbf{Aut}(V)$ of its name in the universe, and the canonical ∞-action of that on $V$ is exhibited the consecutive homotopy pullback

$$\array{ V &\longrightarrow& V/\mathbf{Aut}(V) &\longrightarrow& \widehat Type \\ \downarrow && \downarrow && \downarrow \\ \ast &\stackrel{\vdash V}{\longrightarrow}& \mathbf{B}\mathbf{Aut}(V) &\hookrightarrow& Type } \,.$$

Example

Combining examples and , we get for any $X, A \in \mathbf{H}$ a canonical $\mathbf{Aut}(X)$-$\infty$-action on $[X,A]$ by precomposition. We are interested in studying this for the case that $A$ is a coefficient for differential cohomology, such as $A = \mathbf{B}^{p+1}(\mathbb{R}/\Gamma)_{conn}$.

Definition

Given a $G$-∞-action $\rho$ on some $X$, and given a global element of $X$

$$x \colon \ast \to X$$

then the homotopy stabilizer group $Stab_\rho(x)$ of the $G$-action at $x$ is the loop space object

$$Stab_\rho(x) \coloneqq \Omega_{i(x)} (X/G)$$

of the homotopy quotient of the action at the image $i(x)$ of $x$ under the quotient projection.

Remark

Equivalently, def. , gives the loop space object of the 1-image $\mathbf{B}Stab_\rho(x)$ of the morphism

$$\ast \stackrel{x}{\to} X \to X/G \,.$$

As such the delooping of the stabilizer $\infty$-group sits in a 1-epimorphism/1-monomorphism factorization $\ast \to \mathbf{B}Stab_\rho(x) \hookrightarrow X/G$ which combines with the homotopy fiber sequence of prop. to a diagram of the form

$$\array{ \ast &\stackrel{x}{\longrightarrow}& X &\stackrel{}{\longrightarrow}& X/G \\ \downarrow^{\mathrlap{epi}} && & \nearrow_{\mathrlap{mono}} & \downarrow \\ \mathbf{B} Stab_\rho(x) &=& \mathbf{B} Stab_\rho(x) &\longrightarrow& \mathbf{B}G } \,.$$

In particular there is hence a canonical homomorphism of $\infty$-groups

$$Stab_\rho(x) \longrightarrow G \,.$$

However, in contrast to the classical situation, this morphism is not in general a monomorphism anymore, hence the stabilizer $Stab_\rho(x)$ is not a sub-group of $G$ in general.

Higher Heiseberg-Kostant-Souriau extensions

We consider now homtopy stabilizer groups of higher WZW terms under precomposition action, example , of automorphisms of their domain. Above we considered these terms with coefficients in $\mathbf{B}^{p+1}(\mathbb{R}/\Gamma)_{conn} \in SuperSmooth\infty Grpd$. If we wite $\mathbb{G} \coloneqq \mathbf{B}^{p}(\mathbb{R}/\Gamma)$ then this reads $\mathbf{B}\mathbb{G}_{conn}$. We consier the situation now in this generality (where $\mathbb{G}$ could be any braided ∞-group equipped with a Hodge filtration).

There is one technicality to be aware of:

Definition

For $X \in \mathbf{H}$ write

$$conc \colon [X,\mathbf{B}\mathbb{G}_{conn}] \longrightarrow \mathbb{G}\mathbf{Conn}(X)$$

for the differential concretification of the internal hom.

This is the proper moduli stack of $\mathbb{G}$-principal ∞-connections on $X$ in that a family $U \longrightarrow \mathbb{G}\mathbf{Conn}(X)$ is a vertical $\mathbb{G}$-principal $\infty$-connection on $U \times X\to U$.

Example

For $\mathbf{H} =$Smooth∞Grpd or =FormalSmooth∞Grpd, for $\mathbb{G} = \mathbf{B}^p U(1)$ the circle (p+1)-group with its standard Hodge filtration, then for $X$ any smooth manifold or formal smooth manifold, $(\mathbf{B}^p U(1))\mathbf{Conn}(X)$ is presented via the Dold-Kan correspondence by the sheaf $U \mapsto Ch_\bullet$ of vertical Deligne complexes on $U \times X$ over $U$.

Proposition

For $\mathbb{G} \simeq \mathbf{B}\mathbb{G}'$ then the loop space object of the moduli stack of $\mathbb{G}$-principal $\infty$-connections on $X$ is the moduli stack of flat ∞-connections with gauge group $\Omega \mathbb{G}$

$$\Omega_0 (\mathbb{G}\mathbf{Conn}(X)) \simeq (\Omega\mathbb{G})\mathbf{FlatConn}(X) \,.$$

Proposition

The canonical precomposition ∞-action, example of the automorphism ∞-group $\mathbf{Aut}(X)$ on $[X,\mathbf{B}\mathbb{G}_{conn}]$ passes along $conc$ to an ∞-action on $\mathbb{G}\mathbf{Conn}(X)$.

Definition

Given a $\mathbb{G}$-principal ∞-connection $\nabla \colon X \longrightarrow \mathbf{B}\mathbb{G}_{conn}$ there are the following concepts in higher geometric prequantum theory.

1. The quantomorphism ∞-group is the stabilizer ∞-group of $\nabla \in \mathbb{G}\mathbf{Conn}(X)$, def. , under the $\mathbf{Aut}(X)$-action of ;

   $$\mathbf{QuantMorph}(X,\nabla) \coloneqq \mathbf{Stab}_{\mathbf{Aut}(X)}(conc(\nabla)) \,.$$

2. The Hamiltonian symplectomorphism ∞-group

   $$\mathbf{HamSymp}(X,\nabla) \longrightarrow \mathbf{Aut}(X)$$

   is the 1-image of the canonical morphism $\mathbf{QuantMorph}(X,\nabla) \longrightarrow \mathbf{Aut}(X)$ from remark .

3. A Hamiltonian action of an ∞-group $G$ on $(X,\nabla)$ is an ∞-group homomorphism of the form

   $$\rho \colon G \longrightarrow \mathbf{HamSymp}(X,\nabla) \;$$

4. An ∞-moment map is an $\infty$-group homomorphism

   $$G \longrightarrow \mathbf{QuantMorph}(X,\nabla)$$

5. The Heisenberg ∞-group for a given Hamiltonian $G$-action $\rho$ is the homotopy pullback

   $$\mathbf{Heis}_G(X,\nabla) \coloneqq \rho^\ast \mathbf{QuantMorph}(X,\nabla) \,.$$

Example

For $\mathbf{H} =$ Smooth∞Grpd, for $X \in SmoothMfd \hookrightarrow \mathbf{H}$ a smooth manifold and for $\nabla$ a prequantum line bundle on $X$, then $\mathbf{QuantMorph}(X,\nabla)$ is Souriau’s quantomorphism group covering the Hamiltonian diffeomorphism group. In the case that $(X, F_\nabla)$ is a symplectic vector space $X = V$ regarded as a linear symplectic manifold with Hamiltonian action on itself by translation, then $\mathbf{Heis}_{V}(X,\nabla)$ is the traditional Heisenberg group.

Remark

Since $\mathbf{HamSymp}(X,\nabla)\hookrightarrow \mathbf{Aut}(X)$ is by construction a 1-monomorphism, given any $G$-action $\rho \colon G \longrightarrow \mathbf{Aut}(X)$ on $X$, not necessarily Hamiltonian, then the homotopy pullback $\rho^\ast \mathbf{QuantMorph}(X,\nabla)$ is the Heisenberg ∞-group of the maximal sub-$\infty$-group of $G$ which does act via Hamiltonian symplectomorphisms. Therefore we will also write $\mathbf{Heis}_G(X,\nabla)$ in this case.

The following is the refinement of the Kostant-Souriau extension to higher differential geometry

Proposition

Given a $\mathbb{G}$-principal ∞-connection $\nabla \colon X \longrightarrow \mathbf{B}\mathbb{G}_{conn}$, there is a homotopy fiber sequence of the form

1. if $\mathbb{G}$ is 0-truncated then

   $$\array{ \mathbb{G}\mathbf{ConstFunct}(X) &\longrightarrow& \mathbf{QuantMorph}(X,\nabla) \\ && \downarrow \\ && \mathbf{HamSymp}(X,\nabla) &\stackrel{\mathbf{KS}}{\longrightarrow}& \mathbf{B} (\mathbb{G}\mathbf{ConstFunct}(X)) }$$

2. if $\mathbb{G} \simeq \mathbf{B}\mathbb{G}'$ then

   $$\array{ (\Omega \mathbb{G})\mathbf{FlatConn}(X) &\longrightarrow& \mathbf{QuantMorph}(X,\nabla) \\ && \downarrow \\ && \mathbf{HamSymp}(X,\nabla) &\stackrel{\mathbf{KS}}{\longrightarrow}& \mathbf{B} ((\Omega \mathbb{G})\mathbf{FlatConn}(X)) }$$

exhibiting the quantomorphism ∞-group as an ∞-group extension of the Hamiltonian symplectomorphism ∞-group by the moduli stack of $\Omega \mathbb{G}-$flat ∞-connections, classified by a cocycle $\mathbf{KS}$.

(FRS13a)

Example

In $\mathbf{H} =$ Smooth∞Grpd, let $\mathbb{G} = \mathbf{B}^p U(1)$ be the circle (p+1)-group and let $X \in SmoothMfd \hookrightarrow Smooth \infty Grpd$ be p-connected, then $(\Omega\mathbf{B}^p U(1))\mathbf{FlatConn}(X)\simeq \mathbf{B}^{p}U(1)$. Hence here prop. gives

$$\array{ \mathbf{B}^{p}U(1) &\longrightarrow& \mathbf{QuantMorph}(X,\nabla) \\ && \downarrow \\ && \mathbf{HamSymp}(X,\nabla) &\stackrel{\mathbf{KS}}{\longrightarrow}& \mathbf{B}^{p+1}U(1) }$$

Corollary

Given a $\mathbb{G}$-principal ∞-connection $\nabla \colon X \longrightarrow \mathbf{B}\mathbb{G}_{conn}$, and for $\rho \colon G \longrightarrow \mathbf{HamSymp}(X,\nabla)$ a $G$-Hamiltonian action, then there is a homotopy fiber sequence

1. if $\mathbb{G}$ is 0-truncated then

   $$\array{ \mathbb{G}\mathbf{ConstFunct}(X) &\longrightarrow& \mathbf{Heis}_G(X,\nabla) \\ && \downarrow \\ && G &\stackrel{\mathbf{KS}(\rho)}{\longrightarrow}& \mathbf{B} (\mathbb{G}\mathbf{ConstFunct}(X)) }$$

2. if $\mathbb{G} \simeq \mathbf{B}\mathbb{G}'$ then

   $$\array{ (\Omega \mathbb{G})\mathbf{FlatConn}(X) &\longrightarrow& \mathbf{Heis}_G(X,\nabla) \\ && \downarrow \\ && G &\stackrel{\mathbf{KS}(\rho)}{\longrightarrow}& \mathbf{B} ((\Omega \mathbb{G})\mathbf{FlatConn}(X)) }$$

exhibiting the Heisenberg ∞-group as an ∞-group extension of the $G$ by the moduli stack of $\Omega \mathbb{G}-$flat ∞-connections, classified by a cocycle $\mathbf{KS}(\rho)$.

The class of the cocycle $\mathbf{KS}(\rho)$ is the obstruction to prequantizing $\rho$ to a moment map (the classical anomaly of $\rho$); and the the Heisenberg ∞-group extension of $G$ is the universal cancellation of this anomaly.

Higher Cartan geometry

We consider now the globalization of higher WZW terms on higher group stacks $\tilde G$ to higher manifolds/schemes that are locally modeled on $G$.

For this application we now make use of the fact that the $\infty$-toposes we are interested in are differentially cohesive (dcct) and in particular are equipped with an operation $X \mapsto \Im X$ that sends every stack to its de Rham stack obtained by identifiying infinitesimal neighbour points.

Higher manifolds

Definition

Given $X,Y\in \mathbf{H}$ then a morphism $f \;\colon\; X\longrightarrow Y$ is a local diffeomorphism if its naturality square of the infinitesimal shape modality

$$\array{ X &\longrightarrow& \Im X \\ \downarrow^{\mathrlap{f}} && \downarrow^{\mathrlap{\Im f}} \\ Y &\longrightarrow& \Im Y }$$

is a homotopy pullback square.

Let now $V \in \mathbf{H}$ be given, equipped with the structure of a group (∞-group).

Definition

A $V$-manifold is an $X \in \mathbf{H}$ such that there exists a $V$-atlas, namely a correspondence of the form

$$\array{ && U \\ & \swarrow && \searrow \\ V && && X }$$

with both morphisms being local diffeomorphisms, def. , and the right one in addition being an epimorphism, hence an atlas.

Definition

For $X \in \mathbf{H}$ an object and $x \colon \ast \to X$ a point, then we say that the infinitesimal neighbourhood of, or the infinitesimal disk at $x$ in $X$ is the homotopy fiber $\mathbb{D}^X_x$ of the unit of the infinitesimal shape modality at $x$:

$$\array{ \mathbb{D}^X_x &\longrightarrow& X \\ \downarrow && \downarrow \\ \ast &\stackrel{x}{\longrightarrow}& \im X } \,.$$

Definition

For $X$ any object in differential cohesion, its infinitesimal disk bundle $T_{inf} X \to X$ is the homotopy pullback

$$\array{ T_{inf} X &\stackrel{ev}{\longrightarrow}& X \\ \downarrow^{\mathrlap{p}} && \downarrow \\ X &\longrightarrow& \Im X }$$

of the unit of its infinitesimal shape modality along itself.

Remark

By the pasting law, the homotopy fiber of the infinitesimal disk bundle, def. , over any point $x \in X$ is the infinitesimal disk $\mathbb{D}^X_x$ in $X$ at that point, def.. Nevertheless, for general $X$ the infinitesimal disk bundle need not be an fiber ∞-bundle with typical fiber (the infinitesimal disks at different points need not be equivalent, and even if they are, the bundle need not be locally trivial). Below in prop. we see that for $X$ a $V$-manifold modeled on a group object $V$, then its infinitesimal disk bundle is indeed an fiber ∞-bundle, and hence is the associated ∞-bundle to some principal ∞-bundle. That principal bundle is the frame bundle of $X$.

Lemma

If $\iota \colon U \to X$ is a local diffeomorphism, def. , then

$$\iota^\ast T_{inf} X \simeq T_{inf}U \,.$$

Proof

By the definition of local diffeos and using the pasting law we have an equivalence of pasting diagrams of homotopy pullbacks of the following form:

$$\array{ \iota^\ast T_{inf} X &\longrightarrow& T_{inf} &\longrightarrow& X \\ \downarrow && \downarrow && \downarrow \\ U &\longrightarrow& X &\longrightarrow& \Im X } \;\;\;\; \simeq \;\;\;\; \array{ T_{inf} U &\longrightarrow& U &\longrightarrow& X \\ \downarrow && \downarrow && \downarrow \\ U &\longrightarrow& \Im U &\longrightarrow& \Im X }$$

Definition

For $V$ an object, a framing on $V$ is a trivialization of its infinitesimal disk bundle, def. , i.e. an object $\mathbb{D}^V$ – the typical infinitesimal disk or formal disk, def. , – and a (chosen) equivalence

$$\array{ T_{inf} V && \stackrel{\simeq}{\longrightarrow} && V \times \mathbb{D}^n \\ & \searrow && \swarrow_{\mathrlap{p_1}} \\ && V } \,.$$

Definition

For $V$ a framed object, def. , we write

$$GL(V) \coloneqq \mathbf{Aut}(\mathbb{D}^V)$$

for the automorphism ∞-group of its typical infinitesimal disk/formal disk.

This class of examples of framings is important:

Proposition

Every differentially cohesive ∞-group $G$ is canonically framed (def. ) such that the horizontal map in def. is given by the left action of $G$ on its infinitesimal disk at the neutral element:

$$ev \;\colon\; T_{inf}G \simeq G \times \mathbb{D}^G_e \stackrel{\cdot}{\longrightarrow} G \,.$$

Proof

By the discussion at Mayer-Vietoris sequence in the section Over an ∞-group and using that the infinitesimal shape modality preserves group structure, the defining homotopy pullback of $T_{inf} G$, def. , is equivalent to the pasting of pullback diagrams

$$\array{ T_{inf} G &\stackrel{}{\longrightarrow}& \mathbb{D}^G_e &\stackrel{}{\longrightarrow}& \ast \\ \downarrow && \downarrow && \downarrow \\ G \times G &\stackrel{(-)\cdot (-)^{-1}}{\longrightarrow}& G &\stackrel{}{\longrightarrow}& \Im G }$$

where the right square is the defining pullback for the infinitesimal disk $\mathbb{D}^G$. Finally for the left square we find by this proposition that $T_{inf} G \simeq G\times \mathbb{D}^G$ and that the top horizontal morphism is as claimed.

By lemma it follows that:

Proposition

For $V$ a framed object, def. , let $X$ be a $V$-manifold, def. . Then the infinitesimal disk bundle, def. , of $X$ canonically trivializes over any $V$-cover $V \leftarrow U \rightarrow X$ , i.e. there is a homotopy pullback of the form

$$\array{ U \times \mathbb{D}^V &\longrightarrow& T_{inf} X \\ \downarrow && \downarrow \\ U &\longrightarrow& X } \,.$$

This exhibits $T_{inf} X\to X$ as a $\mathbb{D}^V$-fiber ∞-bundle.

Remark

By this discussion this fiber fiber ∞-bundle is the associated ∞-bundle of an essentially uniquely determined $\mathbf{Aut}(\mathbb{D}^V)$-principal ∞-bundle $Fr(X)$, i.e. there exists a homotopy pullback diagram of the form

$$\array{ T_{inf} X \simeq & Fr(X) \underset{\mathbf{Aut}(\mathbb{D}^V)}{\times} \mathbb{D}^V &\longrightarrow& V//\mathbf{Aut}(\mathbb{D}^V) \\ & \downarrow && \downarrow \\ & X &\stackrel{}{\longrightarrow}& \mathbf{B}\mathbf{Aut}(\mathbb{D}^V) } \,.$$

Definition

Given a $V$-manifold $X$, def. , for framed $V$, def. , then its frame bundle

$$\array{ Fr(X) \\ \downarrow \\ X }$$

is the $GL(V)$-principal ∞-bundle given by prop. via remark .

Remark

By prop. the construction of frame bundles in def. is functorial in formally étale maps between $V$-manifolds.

$G$-Structure

Let $V$ be framed, def. , let $G$ be an ∞-group and $G \to GL(V)$ a homomorphism to the general linear group of $V$, def. , hence

$$G\mathbf{Struc}\colon \mathbf{B}G \longrightarrow \mathbf{B}GL(V)$$

a morphism between the deloopings.

Definition

For $X$ a $V$-manifold, def. , a G-structure on $X$ is a lift of the structure group of its frame bundle, def. , to $G$, hence a diagram

$$\array{ X && \longrightarrow&& \mathbf{B}G \\ & {}_{\mathllap{\tau_X}}\searrow && \swarrow_{\mathrlap{G\mathbf{Struc}}} \\ && \mathbf{B}GL(V) }$$

hence a morphism

$$\mathbf{c} \colon \tau_X \longrightarrow G\mathbf{Struc}$$

in the slice (∞,1)-topos.

In fact $G\mathbf{Struc}\in \mathbf{H}_{/\mathbf{B}GL(n)}$ is the moduli ∞-stack of such $G$-structures.

The double slice $(\mathbf{H}_{/\mathbf{B}GL(n)})_{/G\mathbf{Struc}}$ is the (∞,1)-category of such $G$-structures.

Example

If $V$ is framed, def. , then it carries the trivial $G$-structure, which we denote by

$$\mathbf{c}_0 \colon \tau_{V} \longrightarrow G\mathbf{Struc} \,.$$

Definition

For $V$ framed, def. , and $X$ a $V$-manifold, def. , then a $G$-structure $\mathbf{c}$ on $X$ is integrable (or locally flat) if there exists a $V$-cover

$$\array{ && U \\ & \swarrow && \searrow \\ V && && X }$$

such that the correspondence of frame bundles induced via remark

$$\array{ && \tau_U \\ & \swarrow && \searrow \\ \tau_V && && \tau_X }$$

(a diagram in $\mathbf{H}_{/\mathbf{B}GL(V)}$) extends to a sliced correspondence between $\mathbf{c}$ and the trivial $G$-structure $\mathbf{c}_0$ on $V$, example , hence to a diagram in $\mathbf{H}_{/\mathbf{B}GL(V)}$ of the form

$$\array{ && \tau_U \\ & \swarrow && \searrow \\ \tau_V && \swArrow_{\mathrlap{\simeq}} && \tau_X \\ & {}_{\mathllap{\mathbf{c}_0}}\searrow && \swarrow_{\mathrlap{\mathbf{c}}} \\ && G\mathbf{Struct} }$$

On the other hand, $\mathbf{c}$ is called infinitesimally integrable (or torsion-free) if such an extension exists (only) after restriction to all infinitesimal disks in $X$ and $U$, hence after composition

$$\flat^{rel} U \longrightarrow U$$

with the collection of all infinitesimal disks (the “relative flat modality”), this is also formally étale and hence induces map of frame bundles):

$$\array{ && \tau_{\flat^{rel} U} \\ & \swarrow && \searrow \\ \tau_V && \swArrow_{\mathrlap{\simeq}} && \tau_X \\ & {}_{\mathllap{\mathbf{c}_0}}\searrow && \swarrow_{\mathrlap{\mathbf{c}}} \\ && G\mathbf{Struct} } \,.$$

Definite globalization of WZW terms

The concept of extending a closed differential form defined on a Cartesian space $\mathbb{R}^n$ to a definite form on an $n$-dimensional manifold is familiar from special holonomy manifolds. For instance a definite globalization of the associative 3-form on $\mathbb{R}^7$ to a 7-manifold induces and is induced by a G2-structure. But by the discussion at geometry of physics – prequantum geometry, whenever we see a closed differential form we have to ask whether it is the curvature of a cocycle in differential cohomology, hence we have to ask for a higher prequantization. Here we consider the concept of definite forms prequantized to such definite globalizations of WZW terms.

Proposition

Given a $V$-fiber ∞-bundle $E$ over $X$, and given any coefficient $A$, there is a natural equivalence beween

• morphisms $E \longrightarrow A$;

• sections of the canonically associated ∞-bundle $P \times_{\mathbf{Aut}(V)} [V,A]$ over $X$.

Definition

Given a $V$-fiber ∞-bundle $E$ over $X$, and a global element $x\colon \ast \to V$ then a section $\sigma$ of $E$ is definite on $x$ if there exists a 1-epimorphism $U \to X$ and a diagram

$$\array{ U &\longrightarrow& \ast \\ \downarrow & \swArrow & \downarrow^{\mathrlap{x}} \\ X & \stackrel{\sigma}{\longrightarrow} & V/\mathbf{Aut}(V) \\ & \searrow & \downarrow \\ && \mathbf{B}\mathbf{Aut}(V) } \,.$$

Proposition

Choices of sections definite on $x$ are equivalent to reductions of the structure group along the stabilizer group map $Stab_\mathbf{Aut(V)}(x)\longrightarrow \mathbf{Aut}(V)$.

Definition

Given $\mathbf{c} \colon V \longrightarrow A$, and given a $V$-fiber ∞-bundle $E$ over $X$, then a definite parameterization of $\mathbf{c}$ over $E$ is a $\mathbf{c}^E \colon E \longrightarrow A$ such that the section $\sigma_{\mathbf{c}^X}$ coresponding to it via prop. is definite on $\mathbf{c}$ in the sense of def. .

Definition

For $V$ an ∞-group, $\mathbf{L}\colon V \longrightarrow \mathbf{B}\mathbb{G}_{conn}$ a WZW term, and for $X$ a V-manifold, then a definite globalization of $\mathbf{L}$ over $X$ is

1. A reduction of the structure group, def. , of the frame bundle of $X$ along

   $$\mathbf{Aut}_{Grp}(\mathbb{D}^V) = \mathbf{Aut}^{\ast/}(\mathbf{B}\mathbb{D}^V) \longrightarrow \mathbf{Aut}(\mathbb{D}^V) = GL(V) \,,$$

   for $\mathbb{D}^V$ the infinitesimal disk in $V$;

2. an $\mathbf{L}^X \colon X \longrightarrow \mathbf{B}\mathbb{G}_{conn}$ such that its pullback $T_{inf} X \to X \stackrel{\mathbf{L}^X}{\longrightarrow} \mathbf{B} \mathbb{G}_{conn}$ to the infinitesimal disk bundle of $X$ is definite, def. , on $\mathbf{L}|_{\mathbb{D}^V} \in \mathbb{G}\mathbf{Conn}(\mathbb{D}^V)$, def. .

Since, according to prop. , the second item in def. implies a lift/reduction of the structure group to $\mathbf{QuantMorph}(\mathbf{L}|_{\mathbb{D}^V})$, in total this requires a reduction/lift to the Heisenberg ∞-group

$$G = \mathbf{Heis}_{\mathbf{Aut}_{grp}(\mathbb{D}^V)}(\mathbf{L}|_{\mathbb{D}^V}) \coloneqq \mathbf{QuantMorp}(\mathbf{L}|_{\mathbb{D}^V}) \underset{\mathbf{Aut}(\mathbb{D}^V)}{\times} \mathbf{Aut}_{Grp}(\mathbb{D}^V) \,.$$

This G-structure we require to be first order integrable (with respect to the canonical left-invariant framing of $V$.)

Example

Let $\mathbf{H} =$ Smooth∞Grpd.

1. For $\mathbf{L}\colon T^\ast \mathbb{R}^n \to \mathbf{B}U(1)_{conn}$ the Liouville-Poincaré 1-form $\theta = \sum_{i = 1}^n p_i d q^i$ (regarded as a principal connection on the trivial circle bundle), then a definite globalization of $\mathbf{L}$ is a symplectic manifold equipped with a prequantum line bundle.

2. for $\mathbf{L}\colon \mathbb{R}^7 \longrightarrow \mathbf{B}^3 U(1)_{conn}$ a potential for the associative 3-form, then a definite globalization is a manifold with G2-structure $(X,\omega_3)$ equipped with a bundle gerbe with connection whose 3-form curvature is $\omega_3$.

Example

In $\mathbf{H} =$ SuperFormalSmooth∞Grpd and for $V$ being super Minkowski spacetime of bosonic dimension $d = 3,4,10,11$ regarded as the supersymmetry super-translation group in that dimension, and for $\mathbf{L} = \mathbf{L}$ the WZW term induced by differential Lie integration (here) from the super Lie algebra cocycles of the brane scan in these dimensions, then the Heisenberg ∞-group in def. is a $\mathbf{B}(\mathbb{R}/\Gamma)$-∞-group extension of the Lorentz group in these dimensions.

This means that a choice of definite globalization of $\mathbf{L}_{string}$ over a supermanifold $X$ is in particular a choice of super-orthogonal structure, hence a choice of graviton and of a gravitino field.

The condition that this G-structure be first-order integrable with respect to the canonical left-invariant framing of super Minkowski spacetime then means that the supertorsion of this orthogonal structure vanishes.

For $d = 1$ this is the torsion constraint of supergravity. By (Candiello-Lechner 93, Howe 97) this implies that the above graviton and gravitino field satisfy the Einstein equations for bosonic backgrounds of 11-dimensional supergravity.

This in turn implies in particular that the curvature of the WZW term $\mathbf{L}$ is the fermionic component of the supergravity C-field field strength. This finally means that $\mathbf{L}$ itself is a consistent choice of prequantization of this hence a genuinely globally defined WZW term for the Green-Schwarz sigma model for the M2-brane with target space $X$.

BPS charges

Once a $V$-manifold $X$ is equipped with a definite globalization $\mathbf{L}^X$ of a WZW term $\mathbf{L}$, according to , and hence also with a G-structure $\mathbf{g}$ for $G$ the suitable homotopy stabilizer group of $\mathbf{L}$ on infinitesimal disks, then the automorphism ∞-group $\mathbf{Aut}(X)$ is naturally “broken” to the homotopy stabilizer group of this extra data. The stabilizer of the $G$-structure itself yields the isometry group $\mathbf{Iso}(X,\mathbf{g})$, but since the higher WZW term has in general higher gauge symmetries, the total homotopy stabilizer of the triple $(X,\mathbf{g},\mathbf{L}^{X})$ is a Heisenberg ∞-group extension of that. Since for the case of applications to supergravity (examples , below) the 0-truncation of this ∞-group extension turns out to be the extension by BPS charges, we here speak, for lack of any other established term, generally of BPS charge groups for homotopy stabilizers of definitely globalized higher WZW terms. See (Sati-Schreiber 15) for more.

Definition

Given a definite globalization $\mathbf{L}^X \colon X \longrightarrow \mathbf{B}\mathbb{G}_{conn}$ of a WZW term, def. , hence in particular a G-structure $\mathbf{g}$ on $X$ for $G = \mathbf{Heis}_{\mathbf{Aut}_{grp}(\mathbb{D}^V)}(\mathbf{L}|_{\mathbb{D}^V})$, then the corresponding BPS charge group is the Heisenberg n-group, def. , of $\mathbf{L}^X$ over the isometry group of this $G$-structure:

$$BPS(X,\mathbf{g}, \mathbf{L}) \coloneqq \mathbf{Heis}_{\mathbf{Iso}(X,\mathbf{g})}(X,\mathbf{L}^X) \,.$$

Remark

For $V$ super Minkowski spacetime, then the super L-∞ algebra of $BPS(X,\mathbf{g}, \mathbf{L})$, def. is the Poisson bracket L-∞ algebra $\mathfrak{Pois}(X,\omega)$ of $\omega = F_{\mathbf{L}}$ regarded as a pre-(p+1)-plectic form on $X$. See the discussion in (FRS 13b, section 4).

Consider now two consecutive WZW terms

$$\array{ \widetilde{\hat V} &\stackrel{\mathbf{L}_2}{\longrightarrow}& \mathbf{B}(\mathbb{G}_2)_{conn} \\ \downarrow \\ V &\stackrel{\mathbf{L}_1}{\longrightarrow}& \mathbf{B}(\mathbb{G}_1)_{conn} }$$

with $\mathbf{L}_2$ defined on the differential refinement of the ∞-group extension

$$\array{ \mathbb{G} &\longrightarrow& \hat V \\ && \downarrow \\ && V &\stackrel{}{\longrightarrow}& \mathbf{B}\mathbb{G} }$$

which is the underlying $\mathbb{G}$-principal ∞-bundle underlying $\mathbf{L}_1$.

$$\array{ \widetilde{\hat V} &\stackrel{}{\longrightarrow}& \Omega^1(-,\mathbb{G}) \\ \downarrow &(pb)& \downarrow \\ V &\stackrel{\mathbf{L}_1}{\longrightarrow}& \mathbf{B}(\mathbb{G}_1)_{conn} }$$

Proposition

Given two consecutive WZW terms, $(\mathbf{L}_1,\mathbf{L}_2)$ and given a define globalization, def. , of $\mathbf{L}_1$ over a $V$-manifold $X$ then

1. the isometry action canonically lifts from $X$ to to the extended spacetime $\widetilde {\hat X}$

$$\array{ \widetilde {\hat X} &\longrightarrow& \Omega^1(-\mathbb{G}) \\ \downarrow &(pb)& \downarrow \\ X &\stackrel{\mathbf{L}_1}{\longrightarrow}& \mathbf{B}\mathbb{G}_{conn} } \,;$$

1. the infinitesimal disks in $\widetilde {\hat X}$ are equivalent to those of $\widetilde {\hat V}$.

Definition

By this proposition it is consistent to ask for a consecutive definitite globalization of two consecutive WZW term

$$\array{ \widetilde{\hat X} &\stackrel{\mathbf{L}_2^X}{\longrightarrow}& \mathbf{B}(\mathbb{G}_2)_{conn} \\ \downarrow \\ X &\stackrel{\mathbf{L}_1^X}{\longrightarrow}& \mathbf{B}(\mathbb{G}_1)_{conn} } \,.$$

The BPS charge $\infty$-group of this setup is

$$\mathbf{BPS}(X,\mathbf{g}, \mathbf{L}_1^X, \mathbf{L}_2^X) \coloneqq \mathbf{Heis}_{\mathbf{Iso}(X,\mathbf{g})}(\widetilde {\hat X},\mathbf{L}_2^X) \,.$$

By cor. this is an ∞-group extension of $\mathbf{Iso}(X,\mathbf{g})$ by

$\mathbb{G}_2\mathbf{FlatConn}(\widetilde{\hat X})$. Forgetting the differential part of the twist, this extension group receives a map from $\mathbb{G}_2\mathbf{FlatConn}({\hat X})$.

11d Supergravity with M-brane BPS charges

We now concentrate on the consecutive WZW terms, def. , given, according to The brane bouquet above, by the cocycles $\mu_4$ for the M2-brane, and $\mu_7$ for the M5-brane:

$$\array{ \mathfrak{m}5\mathfrak{brane} \\ \downarrow \\ \mathfrak{m}2\mathfrak{brane} &\stackrel{\mu_7 + h_3\wedge \mu_4}{\longrightarrow}& b^6 \mathbb{R} \\ \downarrow \\ \mathbb{R}^{10,1\vert \mathbf{32}} &\stackrel{\mu_4 \coloneqq \overline{\psi}\Gamma^{a_1 a_2}\wedge \psi \wedge e_{a_1}\wedge e_{a_2}}{\longrightarrow}& b^2 \mathbb{R} }$$

Here $\mathfrak{m}2\mathfrak{brane}$ denotes the “supergravity Lie 3-algebra” regarded as an extended super Minkowski spacetime and $\mathfrak{m}5\mathfrak{brane}$ denotes the “supergravity Lie 6-algebra”. Both hooks $\array{\downarrow \\ & \rightarrow}$ in the diagram are homotopy fiber sequences in the homotopy theory of super L-∞ algebras.

By the discussion in session II, applying differentially refined Lie integration to this yields two consecutive higher WZW terms of the form

$$\array{ \mathbf{B}^{2}(\mathbb{R}/\Gamma_1)_{conn} &\longrightarrow& \widetilde {\hat{\mathbb{R}}}^{10,1\vert \mathbf{32}} &\stackrel{\mathbf{L}_{M5}}{\longrightarrow}& \mathbf{B}^{5} (\mathbb{R}/\Gamma_2)_{conn} \\ && \downarrow \\ && \mathbb{R}^{10,1\vert \mathbf{32}} &\stackrel{\mathbf{L}_{M2}}{\longrightarrow}& \mathbf{B}^2 (\mathbb{R}/\Gamma_1)_{conn} } \,.$$

(Here, by the van Est isomorphism, we do not notationally distinguish super Minkowski spacetime regarded as a super Lie algebra or a super Lie group.)

By example a choice of definite globalization of $\mathbf{L}_{M2}$ is equivalent to bosonic solution $(X,\mathbf{g})$ to the Einstein equations of 11-dimensional supergravity equipped with a compatible globally defined (i.e. classical anomaly free) WZW term $\mathbf{L}_{M2}^X$ for the M2-brane Green-Schwarz sigma model with target space $X$.

By prop. this defines an extended superspacetime $\widetilde{\hat X}$ which is a higher Cartan geometry of locally modeled on the supergravity Lie 3-algebra on which the local M5-brane Green-Schwarz sigma model is defined, and hence may ask for a choice of definite globalization of that

$$\array{ \widetilde {\hat{X}} &\stackrel{\mathbf{L}^X_{M5}}{\longrightarrow}& \mathbf{B}^{5} (\mathbb{R}/\Gamma_2)_{conn} \\ \downarrow \\ X &\stackrel{\mathbf{L}^X_{M2}}{\longrightarrow}& \mathbf{B}^2 (\mathbb{R}/\Gamma_1)_{conn} } \,.$$

This is now a globally well defined background for the M5-brane sigma model and def. determines its BPS-charge super-6-group. By corollary this is a super 6-group extension of the superisometry group of $(X,\mathbf{g})$ by $(\mathbf{B}^5 (\mathbb{R}/\Gamma_2))\mathbf{FlatConn}(\widetilde{\hat X})$.

By the discussion at geometry of physics – WZW terms – Consecutive WZW terms the extended spacetime $\widetilde {\hat X}$ here is such that smooth maps into it

$$\Sigma \longrightarrow \widetilde{\hat X}$$

(which are the fields of the M5-brane sigma model with WZW term $\mathbf{L}^X_{M5}$) are equivalently pairs, consisting of

1. a smooth function $\phi \colon \Sigma \longrightarrow X$ into the actual spacetime $X$;

2. a cocycle $\nabla$ in $\phi$-twisted degree-3 Deligne cohomology on $\Sigma$, hence a 2-form gauge field on $\Sigma$, subject to certain compatibility conditions with the function $\phi$.

The first item here is the evident sigma model field, the second 2-form field is part of the “tensor multiplet” on the M5-brane, exhibiting the Green-Schwarz sigma-model for the M5-brane as a higher gauged WZW model.

Now to consider the BPS charge group of $\mathbf{L}^X_{M5}$, def. . By corollary this is an ∞-group extension of the super-isometry group of the 11-dimensional super spacetime by the moduli stack $(\mathbf{B}^5 U(1))\mathbf{FlatConn}(\widetilde{\hat X})$ of flat 5-form connection on the extended spacetime.

This receives a map $(\mathbf{B}^5 U(1))\mathbf{FlatConn}(\hat X) \longrightarrow (\mathbf{B}^5 U(1))\mathbf{FlatConn}(\widetilde{\hat X})$ from the moduli of 5-form connections of the extended spacetime $\hat X$ (which is $\widetilde{\hat X}$. This consists of the cohomological data without the differential cohomologica data in $\mathbf{L}_{M2}^X$): it is the $\mathbf{B}^2 (\mathbb{R}/\Gamma_1)$-principal ∞-bundle which sits in the homotopy fiber sequence of the form

$$\array{ \mathbf{B}^2 (\mathbb{R}/\Gamma_1) &\longrightarrow& \hat X \\ && \downarrow \\ && X &\stackrel{\mathbf{DD}(\mathbf{L}_{M2}^X)}{\longrightarrow}& \mathbf{B}^3 (\mathbb{R}/\Gamma_1) } \,.$$

Under Lie differentiation and via prop. , $(\mathbf{B}^5 U(1))\mathbf{FlatConn}(\widetilde{\hat X})$ turns into $(\mathbf{B}^5 \mathbb{R})\mathbf{FlatConn}(\widetilde{\hat X})$ hence into $\mathbf{H}(\hat X, \flat \mathbf{B}^5 \mathbb{R})$. Under the adjunction between shape modality $\int$ and flat modality $\flat$, this is the degree-5 real cohomology of the geometric realization of $\hat X$. This in turns is a K(Z,3)-fibration $\int \hat X \to \int X$ over the underlying bare homotopy type of spacetime $X$ which is classified by the integral degree-4 class which is the higher Dixmier-Douady class $DD(\mathbf{L}_{M5}^X)$ of $\mathbf{L}_{M2}^{X}$.

The degree-5 real cohomology of such a fibration is computed by a Serre spectral sequence. By the discussion at Eilenberg-MacLane space – cohomology of EM spaces only very few entries in this spectral sequence contribute, and the result is the middle cohomology of this sequence

$$H^1(X) \stackrel{(0,d_4)}{\longrightarrow} H^2(X) \oplus H^5(X) \stackrel{(d_4,0)}{\longrightarrow} H^6(X)$$

where $d_4 \propto (-)\cup DD(\mathbf{L}_{M2}^X)$ is given by taking the cup product with the class of the M2-WZW term.

This is the group of M2-brane and M5-brane charges with corrections by global effects, in the corrected M-theory super Lie algebra for the superspacetime $(X,g)$.

Compactification on $G_2$-manifolds and M2-instanton contributions

We saw above in example an intimate analogy between G2-manifold structure and solutions to 11-dimensional supergravity, both come from globalizing a local form to a definite form in a torsion-free way:

1. A torsion-free definite globalization of the associative 3-form $\alpha$ on $\mathbb{R}^7$ is a G2-manifold;

2. a torsion-free definite globalization of the M2-brane cocycle $curv(\mathbf{L}_{M2}) = \overline{\psi} \Gamma^{a b} \wedge \psi \wedge e_a \wedge e_b$ on $\mathbb{R}^{10,1\vert \mathbf{32}}$ is a solution to the Einstein equations of motion of 11-dimensional supergravity.

It is possible and natural to combine these two phenomena: if we consider coefficients not just in $\mathbb{R}/\Gamma$ but in the complexification $\mathbb{C}/\Gamma$, then there is the complex linear combination of both terms to a complex 2-gerbe:

$$\mathbf{L}_{M2} + i \alpha \;\colon\; \mathbb{R}^{10,1\vert\mathbf{32}} \longrightarrow \mathbf{B}^{3} (\mathbb{C}/\mathbb{Z})_{conn} \,,$$

where we regard $\alpha$ as a 3-form on $\mathbb{R}^{10,1} \simeq \mathbb{R}^{3,1}\oplus \mathbf{R}^7$ coming from the second summand, and then regard it as a closed connection 3-form for a 2-gerbe.

Now a definite globalization $\mathbf{L}^X_{M2} + i \alpha^X$ of $\mathbf{L}_{M2} + i \alpha$ enforces both the above constraints, hence is given by 11-dimensional super spacetimes $(X,g)$ that solve the Einstein equations of motion and which are fibered by G2-manifolds.

This is precisely the setup of the situation of interest in string phenomenology, see at M-theory on G2-manifolds. In fact since we are globalizing in higher differential geometry, the globalizations may carry orbifold singularities, just as needed for the conjectured phenomenon of gauge enhancement.

More is true: since the globalization of $\alpha$ over a G2-manifold is a calibration, and since supersymmetric 3-cycles in $G_2$-manifolds come from associative submanifolds, which are the calibrated submanifolds, it follows that the volume holonomy of $\mathbf{L}_{M2} + i \alpha$ on M2-branes that are wrapped on such cycles $c_3$ is precisely the membrane instanton contribution

$$hol_{c_3}(\mathbf{L}^X_{M2} + i \alpha^X) = hol_c_{3}(C_3) + i vol_{c_3}(g) \,.$$

References

We give detailed pointers to the literature in the above text. Here we just list the original articles that the above lecture notes are based on.

$\,$

• John Baez, Alissa Crans, Urs Schreiber, Danny Stevenson, From loop groups to 2-groups, Homology Homotopy Appl. Volume 9, Number 2 (2007), 101-135. (arXiv:math/0504123)

• Hisham Sati, Urs Schreiber, Jim Stasheff, L-infinity algebra connections and applications to String- and Chern-Simons n-transport, in Quantum Field Theory, Birkhäuser (2009) 303-424 (arXiv:0801.3480)

• Hisham Sati, Geometric and topological structures related to M-branes, part I, Proc. Symp. Pure Math. 81 (2010), 181-236 (arXiv:1001.5020)

• Domenico Fiorenza, Urs Schreiber, Jim Stasheff, Cech Cocycles for Differential characteristic Classes, Adv. in Theor. and Mathem. Physics, Volume 16 Issue 1 (2012), pages 149-250 (arXiv:1011.4735)

• Hisham Sati, Urs Schreiber, Jim Stasheff, Twisted Differential String and Fivebrane Structures, Communications in Mathematical Physics, Volume 315, Issue 1 (2012) (arXiv:0910.4001)

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, The moduli 3-stack of the C-field, Communications in Mathematical Physics, Volume 333, Issue 1 (2015), Page 117-151 (arXiv:1202.2455)

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, Multiple M5-branes, String 2-connections, and 7d nonabelian Chern-Simons theory, Advances in Theoretical and Mathematical Physics, Volume 18, Number 2 (2014) (arXiv:1201.5277)

• Thomas Nikolaus, Urs Schreiber, Danny Stevenson, Principal ∞-bundles – General theory, Journal of Homotopy and Related Structures, Volume 10, Issue 4 (2015) (arXiv:1207.0248)

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, Super Lie $n$-algebra extensions, higher WZW models and super $p$-branes with tensor multiplet fields, International Journal of Geometric Methods in Modern Physics, Volume 12, Issue 02 (2015) 1550018 (arXiv:1308.5264)

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, The WZW term of the M5-brane, J. Math. Phys. 56, 102301 (2015) (arXiv:1506.07557)

• Domenico Fiorenza, Chris Rogers, Urs Schreiber, Higher geometric prequantum theory (arXiv:1304.0236)

• Domenico Fiorenza, Chris Rogers, Urs Schreiber, $L_\infty$-algebras of local observables from higher prequantum bundles, Homology, Homotopy and Applications, Volume 16 (2014) Number 2, p. 107 ? 142 (arXiv:1304.6292)

• Hisham Sati, Framed M-branes, corners, and topological invariants, (arXiv:1310.1060)

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, The WZW term of the M5-brane and differential cohomotopy, J. Math. Phys. 56, 102301 (2015) (arXiv:1506.07557)

• Hisham Sati, Urs Schreiber, Lie n-algebras of BPS charges (arXiv:1507.08692)

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, Rational sphere valued supercocycles in M-theory, to appear in Journal of Geometry and Physics (arXiv:1606.03206)

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, T-Duality from super Lie n-algebra cocycles for super p-branes (arXiv:1611.06536)

• John Huerta, Urs Schreiber, M-Theory from the Superpoint

• Urs Schreiber, differential cohomology in a cohesive topos

• Urs Schreiber, Igor Khavkine, Lie n-algebras of higher Noether currents