nLab first stable homotopy group of spheres

Idea

The first stable homotopy group of spheres (the first stable stem) is the cyclic group of order 2:

(1)$$\array{ \pi_1^s &\simeq& \mathbb{Z}_{/2} \\ [h_{\mathbb{C}}] &\leftrightarrow& [1] }$$

where the generator $[1] \in \mathbb{Z}/2$ is represented by the complex Hopf fibration $S^3 \overset{h_{\mathbb{C}}}{\longrightarrow} S^2$ (cf. Prop. below).

from SS21

Properties

Generator

Proposition

A generator of $\pi_1^s$, is represented by the suspension of the complex Hopf fibration.

Proof

Assuming we know the relevant homotopy groups of spheres, and that $h_{\mathbb{C}}$ generates $\pi_3(S^2)$, then (the boundary case of) the Freudenthal suspension theorem implies that

$$\mathbb{Z} \simeq \pi_3(S^2) \overset{\Sigma}{\longrightarrow} \pi_4(S^3) \simeq \mathbb{Z}_{/2}$$

is surjective, hence that the generator $h_{\mathbb{C}}$ is sent to a generator $\Sigma h_{\mathbb{C}}$.

As the first framed bordism group

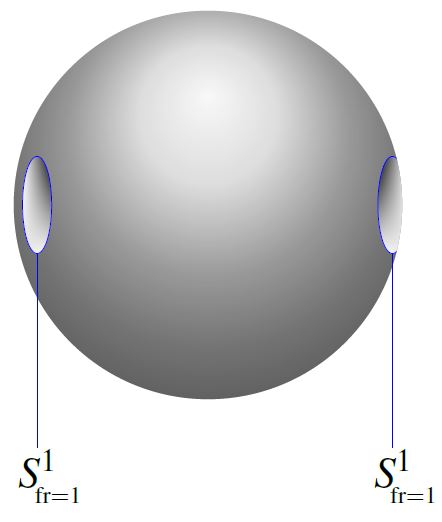
Under the Pontrjagin-Thom isomorphism, identifying the stable homotopy groups of spheres with the bordism ring $\Omega^{fr}_\bullet$ of stably framed manifolds (see at MFr), the generator (1) is represented by the 1-sphere (with its left-invariant framing induced from the identification with the Lie group U(1))

$$\array{ \pi_1^s & \simeq & \Omega_1^{fr} \\ [h_{\mathbb{C}}] & \leftrightarrow & [S^1_{fr=1}] \,. }$$

Moreover, the relation $2 \cdot [S^1_{Lie}] \,\simeq\, 0$ is represented by the bordism which is the complement of 2 open balls inside the 2-sphere.

Related concepts

• complex Hopf fibration

• second stable homotopy group of spheres

• third stable homotopy group of spheres

• seventh stable homotopy group of spheres

• homotopy groups of spheres in HoTT

References

The original computation via Pontryagin's theorem in cobordism theory:

• Lev Pontrjagin, Classification of continuous maps of a complex into a sphere, Communication I, Doklady Akademii Nauk SSSR 19(3) (1938), 147-149

with a more comprehensive account in:

• Lev Pontrjagin, Section 14 of: Smooth manifolds and their applications in homotopy theory, Trudy Mat. Inst. im Steklov, No 45, Izdat. Akad. Nauk. USSR, Moscow, 1955 (AMS Translation Series 2, Vol. 11, 1959) (doi:10.1142/9789812772107_0001)

Early comprehensive discussion:

• Hirosi Toda; p. 186 of: Composition Methods in Homotopy Groups of Spheres, Annals of Mathematics Studies 49, Princeton University Press (1962) [doi:10.1515/9781400882625, jstor:j.ctt1bgzb5t]

See also:

• Mehmet Kirdar, On the First, the Second and the Third Stems of the Stable Homotopy Groups of Spheres [arXiv:2107.06103]

Review:

• Daniel Freed, Karen Uhlenbeck, Appendix B of: Instantons and Four-Manifolds, Mathematical Sciences Research Institute Publications, Springer 1991 (doi:10.1007/978-1-4613-9703-8)

• Guozhen Wang, Zhouli Xu, Section 2.3 of: A survey of computations of homotopy groups of Spheres and Cobordisms, 2010 (pdf)

• Andrew Putman, Section 5 of: Homotopy groups of spheres and low-dimensional topology (pdf, pdf)

Discussion in homotopy type theory:

• Guillaume Brunerie: On the homotopy groups of spheres in homotopy type theory [arxiv:1606.05916]

and on the implementation of the computation in cubical Agda:

• Axel Ljungström, The Brunerie Number Is -2 (June 2022) [blog entry]

• Anders Mörtberg: Computational Proofs in Synthetic Homotopy Theory, talk at Running HoTT 2024, CQTS@NYUAD (April 2024) [video:kt]

• András Kovács: Efficient Evaluation for Cubical Type Theories, talk at Running HoTT 2024, CQTS@NYUAD (April 2024) [video:kt, slides:pdf]