nLab Reissner-Nordström spacetime
Context
Gravity
Formalism
Definition
Spacetime configurations
Properties
Spacetimes
| black hole spacetimes | vanishing angular momentum | positive angular momentum |
|---|---|---|
| vanishing charge | Schwarzschild spacetime | Kerr spacetime |
| positive charge | Reissner-Nordstrom spacetime | Kerr-Newman spacetime |
Quantum theory
Physics
physics, mathematical physics, philosophy of physics
Surveys, textbooks and lecture notes
theory (physics), model (physics)
experiment, measurement, computable physics
-
-
-
Axiomatizations
-
Tools
-
Structural phenomena
-
Types of quantum field thories
-
Contents
Idea
The Reissner-Nordström solution to the equations of motion of Einstein-Maxwell theory describes the spacetime outside of a electrically charged (and/or magnetically charged) point mass, hence describes a charged black hole.
Details
Metric
For mass , electric charge and magnetic charge the pseudo-Riemannian metric for the Reissner-Nordström spacetime is, in polar coordinates on , given by
where (in natural units)
The corresponding Faraday tensor/electromagnetic field strength curvature 2-form is
(check sign)
Horizons
The function above vanishes at
The larger of the two solutions is an event horizon, the other is a Cauchy horizon. In the case that they coincide, for , one speaks of an extremal black hole (at least when also ).
Properties
Penrose diagrams
The Penrose diagram for maximally extended RN black holes (from HE 73, Section 5.5):
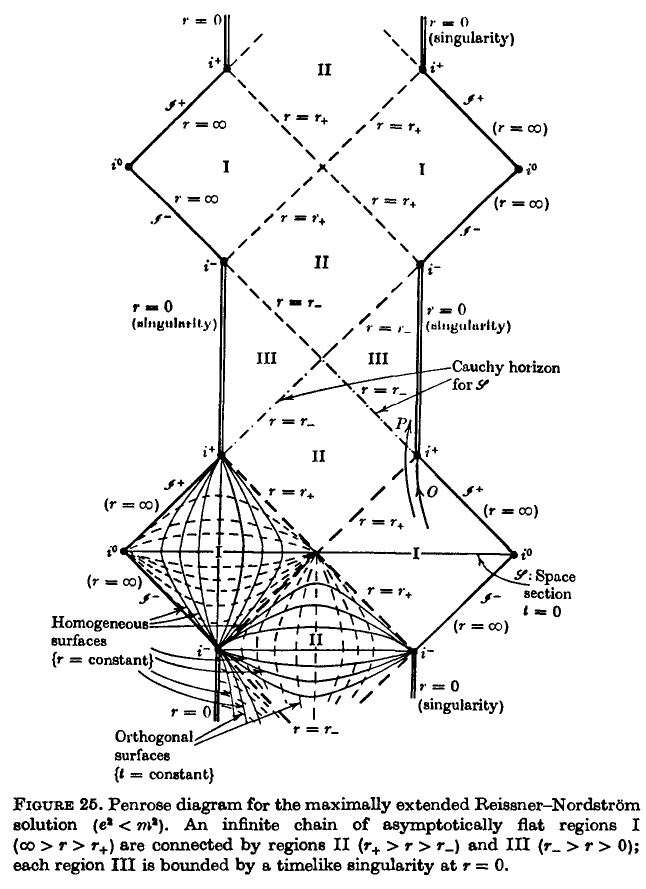
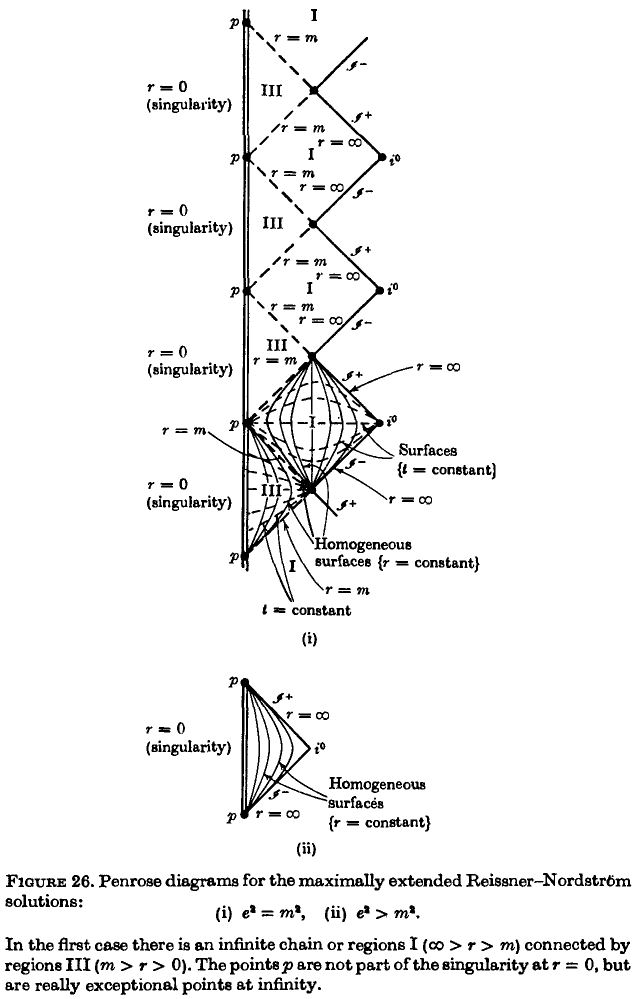
Interior solutions
Instead of having a mass and charge of singular support at the singular locus of the RN-spacetime, one may consider a finite mass and charge distribution, i.e. a “charged star”. Outside of this mass/charge distribution then the metric is the RN-spacetime as above, but in the interior it becomes smoothed out to a non-singular interior solution.
Several attempts have been made to round out the Reissner metric with an interior. Tiwari-Rao-Kanakamedala 85 found an interior with the condition , which obviously holds for the exterior Reissner, but does not match the interior Schwarzschild solution for e = 0. Kyle-Martin 67 found a rather complicated solution. They discussed the self-energy of the fields of charged matter. Wilson 69 modified this solution assuming a different value for the total charge. Cohen-Cohen 69 applied this solution to the special case of a charged thin shell and showed that the energy density of the electromagnetic field contributes to the mass. Boulware 73 studied the time development of thin shells. Graves-Brill 60 considered a possible oscillatory character of the Reissner-Nordström metric by examining the metric by Kruskal-like coordinates Bekenstein 71 studied another ansatz for the stress-energy-tensor of charged matter. Krori-Jayantimala 75 made use of the same ansatz, and he found a solution free of singularities. Gautreau-Hoffman 73 studied the sources of Weyl-type electrovac fields. They obtained the parameters for the source with the junction condition for the exterior solution. Efinger 64 deduced the stability of a charged particle from the self-energy of the gravitation field. In Burghardt 09 is constructed another interior solution with the help of embedding the geometry in a 5-dimensional flat space.
(Literature summary taken from Burghardt 09)
See also (Mehra 82, WX 87, Gupta-Kumar-Pratibha 12).
Related concepts
| black hole spacetimes | vanishing angular momentum | positive angular momentum |
|---|---|---|
| vanishing charge | Schwarzschild spacetime | Kerr spacetime |
| positive charge | Reissner-Nordstrom spacetime | Kerr-Newman spacetime |
References
Original articles:
- Hans Reissner, Über die Eigengravitation des elektrischen Feldes nach der Einstein’schen Theorie, Annalen der Physik 50 pp. 106–120, 1916 (doi:10.1002/andp.19163550905, pdf, atticus)
Review:
-
Jonatan Nordebo, The Reissner-Nordström metric, 2016 (pdf, diva2:912393)
-
Wikipedia, Reissner-Nordström metric
-
Reissner-Nordström geometry [astronuclphysics.info/Gravitace3-5.htm]
That the near horizon geometry of the extremal Reissner-Nordström black hole in 4d ins 2d anti de Sitter spacetime times the 2-sphere, , was observed in
- Gary Gibbons, in F. del Aguila, J. de Azcarraga, Luis Ibanez (eds.) Supersymmetry, Supergravity and Related Topics
Discussion of interior solutions:
-
Graves J. C., Brill D. R., Oscillatory character of Reissner-Nordström metric for an ideal charged wormehole. Phys. Rev. 120, 1507, 1960
-
Efinger H. J., Der kugelsymmetrische Fall einer statischen Ladungsverteilung bei stark komprimierter Materie in der allgemeinen Relativitätstheorie. Acta Phys. Austr. 17, 347, 1964.
Über die Selbstenergie und Ladung eines durch Gravitationswirkung stabilisierten Teilchens in einem gekrümmten Raum, Acta Phys. Austr. 188, 31, 1965
-
Kyle C. F., Martin A. W., Self-energy considerations in general relativity and the exact fields of charge and mass distribution, Nuov. Cim 50, 883, 1967
-
Cohen J. M., Cohen M. D., Exact fields of charge and mass distributions in general relativity. Nuov. Cim. 60, 241, 1969
-
Wilson, S. J., Exact solution of a static charged sphere in general relativity. Can. Journ. Phys. 47, 2401, 1969
-
Jacob Bekenstein, Hydrostatic equilibrium and gravitational collapse of relativistic charged fluid balls, Phys. Rev. D 4, 2185, 1971
-
S. W. Hawking, G. F. R. Ellis, Section 5.5 of: The Large Scale Structure of Space-Time, Cambridge University Press (1973) (doi:10.1017/CBO9780511524646)
-
Boulware, D. G., Naked singularities, thin shells, and the Reissner-Nordström metric, Phys. Rev. D 8, 2363, 1973
-
Gautreau R., Hoffman R. B., The structure of Weyl-type electrovac fields in general relativity. Nouv. Cim. 16 B, 162, 1973
-
Krori K. D., Jayantimala B., A singularity-free solution for a charged fluid in general relativity, J. Phys. A 8, 508, 1975
-
A.L. Mehra, An interior solution for a charged sphere in general relativity, Physics Letters A Volume 88, Issue 4, 8 March 1982, Pages 159-161 (publisher)
-
Tiwari R. N., Rao J. R., Kanakamedala R. R., Electromagnetic mass models in general relativity, Phys. Rev. D 30, 489, 1984
-
Wang Xingxiang, Exact Solution of a Static Charged Sphere in General Relativity, General Relativity and Gravitation, Vol. 19, No. 7, 1987
-
Rainer Burghardt, Reissner exterior and interior arXiv:0902.0918
-
Gupta, Y. K.; Kumar, Jitendra; Pratibha, A Class of Well Behaved Charged Analogues of Schwarzchild’s Interior Solution, International Journal of Theoretical Physics October 2012, Volume 51, Issue 10, pp 3290–3302 (publisher)
Discussion of magnetic black holes (similar to magnetic monopoles):
- Juan Maldacena, Comments on magnetic black holes, J. High Energ. Phys. 2021 79 (2021) [arXiv:2004.06084, doi:10.1007/JHEP04(2021)079]
On approximating Schwarzschild black holes as bound states of Reissner-Nordström black holes:
- Raphaël Dulac, Pierre Heidmann: Building the Blocks of Schwarzschild [arXiv:2404.18994]
Last revised on August 1, 2024 at 05:22:08. See the history of this page for a list of all contributions to it.