nLab annular braid group

Idea

The annular braid group or circlular braid group $CBr_n$ (cf. Bellingeri & Bodin 2014 p 1) on $n \in \mathbb{N}$ strands is the surface braid group of the annulus, hence the fundamental group of the configuration space of $n$-points inside the annulus.

Properties

Definition

The affine type A braid group $Br_n^{aff}$ has generators and relations given by the same formulas as for the Artin presentation of the ordinary braid group $Br_n$, except that the indices in these formulas are identified modulo $n$.

Proposition

The annular braid group is isomorphic to a semidirect product

(1)$$CBr_n \,\simeq\, Br_n^{aff} \rtimes \underset { \mathbb{Z} } { \underbrace{ \langle c \rangle } }$$

of the affine braid group (Def. ) generated by Artin Generators $b_i$ with the group of integers, the latter generated by the braid $c$ which exhibits a 1-step cyclic permutation around the inner boundary of the annulus.

(Kent & Pfeifer 2002 Thm 1, cf. Gadbled, Thiel & Wagner 2015 Rem. 1.1).

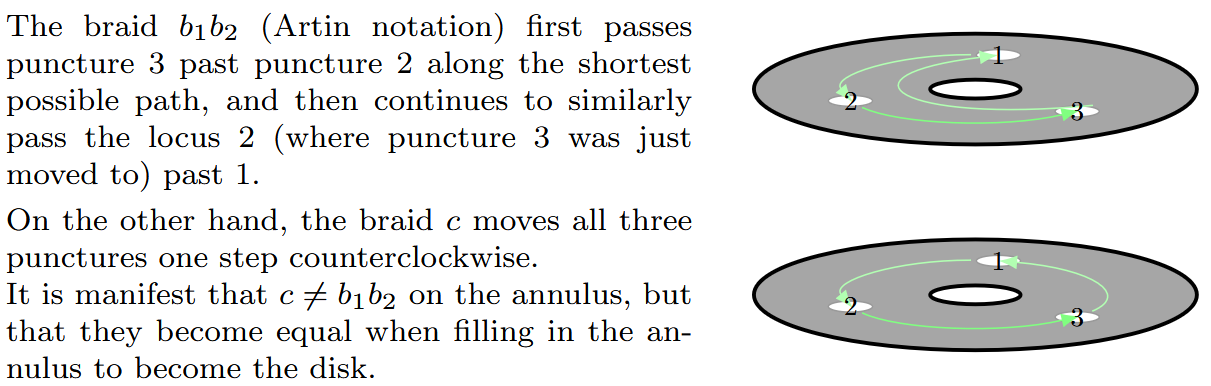
Remark

The mapping class group of the $n$-punctured annulus the further semidirect product of (1) with another copy of $\mathbb{Z}$:

$$MCG(\mathbb{A}, n) \,\simeq\, CBr_n \rtimes \mathbb{Z} \,\simeq\, Br_n^{aff} \rtimes \mathbb{Z}^2 \,.$$

(Gadbled, Thiel & Wagner 2015 Rem. 1.2)

In fact, it should even be a direct product

$$MCG(\mathbb{A}, n) \,\simeq\, CBr_n \times \underset { \mathbb{Z} } { \underbrace{ \langle d\rangle } }$$

because (by arguments as in Bellingeri & Gervais 2012, cf. MO:q/488784) the extra generator $d$ (the annulus Dehn twist) may be taken to leave all the punctures fixed:

References

• Richard P. Kent, David Pfeifer: A Geometric and algebraic description of annular braid groups, International Journal of Algebra and Computation 12 01n02 (2002) 85-97 [doi:10.1142/S0218196702000997]

• Paolo Bellingeri, Arnaud Bodin: The braid group of a necklace, Mathematische Zeitschrift 283 3 (2014) [arXiv:1404.2511, doi:10.1007/s00209-016-1630-0]

• Paolo Bellingeri, pp 4 of: Surface braids and mapping class group II Braid groups on surfaces of genus 0: group presentations, definitions and torsion elements [pdf]

• Agnes Gadbled, Anne-Laure Thiel, Emmanuel Wagner: Categorical action of the extended braid group of affine type A, Communications in Contemporary Mathematics 19 03 (2017) 1650024 [arXiv:1504.07596, doi;10.1142/S0219199716500243]