nLab anti de Sitter spacetime

Skip the Navigation Links | Home Page | All Pages | Latest Revisions | Discuss this page |
Redirected from "anti de Sitter spacetimes".
Contents

Context

Riemannian geometry

Gravity

gravity, supergravity

Formalism

Definition

Spacetime configurations

Properties

Spacetimes

Quantum theory

Contents

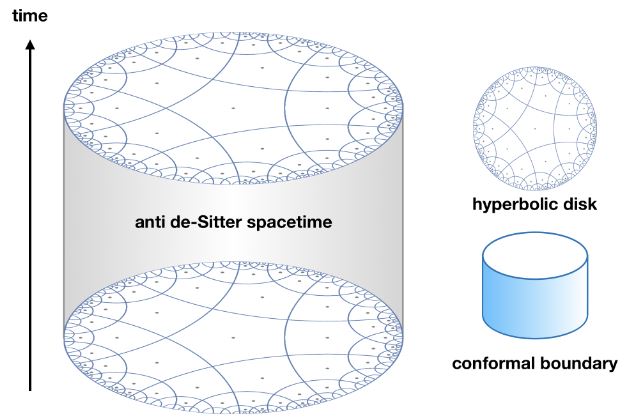
Definition

Up to isometry, the anti de Sitter spacetime of dimension dd, AdS dAdS_d, is the pseudo-Riemannian manifold whose underlying manifold is the submanifold of the Minkowski spacetime ℝ d−1,2\mathbb{R}^{d-1,2} that solves the equation

∑ i=1 d−1(x i) 2−(x d) 2−(x 0) 2=−R 2, \textstyle{\sum_{i = 1}^{d-1}} (x_i)^2 - (x_d)^ 2 - (x_0)^2 \;=\; - R^2 \,,

for some R≠0R \neq 0 (the “radius” of the spacetime) and equipped with the metric tensor induced from the ambient metric, where {x 0,x 1,x 2,⋯,x d}\{x^0, x^1, x^2, \cdots, x^d\} denote the canonical coordinates. AdS dAdS_d is homeomorphic to ℝ d−1×S 1\mathbb{R}^{d-1} \times S^1, and its isometry group is O(d−1,2)O(d-1, 2).

More generally, one may define the anti de Sitter space of signature (p,q)(p,q) as isometrically embedded in the space ℝ p,q+1\mathbb{R}^{p,q+1} with coordinates (x 1,...,x p,t 1,…,t q+1)(x_1, ..., x_p, t_1, \ldots, t_{q+1}) as the sphere ∑ i=1 px i 2−∑ j=1 q+1t j 2=−R 2\sum_{i=1}^p x_i^2 - \sum_{j=1}^{q+1} t_j^2 = -R^2.

graphics grabbed from Yan 19

Properties

Coordinate charts

A comprehesive account of the AdS metric tensor in various coordinate charts is given in Blau §39.3.


Poincaré and horospheric coordinates (e.g. Blau §39.3.7). Consider the Cartesian space ℝ 1+p\mathbb{R}^{1+p} with its canonical coordinate functions

X a:ℝ 1+p→−ℝ,a∈{0,1,⋯,p} X^a \;\colon\; \mathbb{R}^{1+p} \xrightarrow{\phantom{-}} \mathbb{R} \,, \;\;\; a \in \{0,1,\cdots, p\}

and denote its standard Minkowski metric tensor by

ds ℝ 1,p 2≔∑ a=0 pdX a⊗dX a. d s^2_{\mathbb{R}^{1,p}} \;\coloneqq\; \textstyle{\sum_{a = 0}^p} \mathrm{d}X^a \otimes \mathrm{d}X^a \,.

Moreover consider ℝ 1+p×ℝ >0\mathbb{R}^{1+p} \times \mathbb{R}_{\gt 0} equipped with the pullback of the above coordinate function as well as with

r:ℝ 1+p×ℝ >0↠ℝ >0↪ℝ. r \;\colon\; \mathbb{R}^{1+p} \times \mathbb{R}_{\gt 0} \twoheadrightarrow \mathbb{R}_{\gt 0} \hookrightarrow \mathbb{R} \,.

Then there is a chart of AdS p+2AdS_{p+2} of the form

ι:ℝ 1+p×ℝ >0↪−−AdS p+2 \iota \;\colon\; \mathbb{R}^{1+p} \times \mathbb{R}_{\gt 0} \xhookrightarrow{\phantom{--}} AdS_{p+2}

such that the pullback of the AdS metric tensor is

(1)ι *ds AdS 2=r 2R 2ds ℝ 1,d 2+R 2r 2dr 2. \iota^\ast \mathrm{d}s^2_{AdS} \;=\; \tfrac{r^2}{R^2} \mathrm{d}s^2_{\mathbb{R}^{1,d}} \,+\, \tfrac{R^2}{r^2} \mathrm{d}r^2 \,.

This is the form of the AdS-metric which arises naturally as the near horizon geometry of black p-branes in supergravity (e.g. AFFHS98 (5)). The black brane singularity itself would be at r=0r = 0.

In slight variation, in terms of

z≔1/r,hencer=z −1,dr=−1z 2dz z \,\coloneqq\, 1/r \,, \;\;\; \text{hence} \;\;\; r = z^{-1} \,, \;\; \mathrm{d}r \;=\; -\tfrac{1}{z^2} \mathrm{dz} \;\;

the metric (1) becomes

(2)ι *ds AdS 2=R 2z 2(1R 4ds ℝ 1,d 2+dz 2). \iota^\ast \mathrm{d}s^2_{AdS} \;=\; \frac{R^2}{z^2} \big( \tfrac{1}{R^4} \mathrm{d}s^2_{\mathbb{R}^{1,d}} \,+\, \mathrm{d}z^2 \big) \,.

cf. e.g. Bayona & Braga 2007 (11). (These are called horospheric coordinates by Gibbons 2000 (12).)

On the other hand, in terms of

ρ≔lnr,hencer=e ρ,dr=rdρ \rho \;\coloneqq\; ln r \,, \;\; \text{hence} \;\; r = e^\rho \,, \;\; \mathrm{d}r = r \, \mathrm{d}\rho

the metric (1) becomes

(3)ι *ds AdS 2=e 2ρR 2ds ℝ 1,d 2+R 2dρ 2. \iota^\ast \mathrm{d}s^2_{AdS} \;=\; \tfrac{e^{2\rho}}{R^2} \mathrm{d}s^2_{\mathbb{R}^{1,d}} \,+\, R^2 \mathrm{d}\rho^2 \,.

This is called horospheric coordinates in arXiv:1412.2054 (37).


Cartan geometry

We spell out the curvature tensors of anti de Sitter spacetime, using a Cartan connection (i.e. first order formulation).

An evident choice of an orthonormal coframe field for the AdS metric in Poincaré coordinates (1) is

E a ≔ rRdX a a∈{0,1,⋯,d} E p′ ≔ Rrdr \begin{array}{ccll} E^a &\coloneqq& \tfrac{r}{R} \mathrm{d}X^a & a \in \{0,1, \cdots, d\} \\ E^{p'} &\coloneqq& \tfrac{R}{r} \mathrm{d}r \end{array}

in that

ι *ds AdS p+2 2=η abE a⊗E b+E p′⊗E p′. \iota^\ast \mathrm{d}s^2_{AdS_{p+2}} \;=\; \eta_{a b} E^a \otimes E^b + E^{p'} \otimes E^{p'} \,.

(no sum over p′p' – this is meant to be the index value corresponding to the radial direction)

The torsion-free spin connection Ω\Omega for this coframe field, characterized by

(4)dE a = Ω a bE b dE p′ = Ω p′ bE b, \begin{array}{ccl} \mathrm{d}E^a &=& \Omega^a{}_b \, E^b \\ \mathrm{d}E^{p'} &=& \Omega^{p'}{}_b \, E^b \mathrlap{\,,} \end{array}

has non-vanishing components

Ω ap′=−Ω p′a=−rR 2dX a. \Omega^{a p'} \,=\, - \Omega^{p' a} \;=\; - \tfrac{r}{R^2} \mathrm{d}X^a \,.

The corresponding curvature 2-form

R a 1a 2=−Ω a 1 p′Ω p′a 2 R ad′≔dΩ ap′ \begin{array}{l} R^{a_1 a_2} \;=\; - \Omega^{a_1}{}_{p'} \Omega^{p' a_2} \\ R^{a d'} \;\coloneqq\; \mathrm{d}\Omega^{a p'} \end{array}

has non-vanishing components

R a 1a 2=−r 2R 4dX a 1dX a 2=−1R 2E a 1E a 2 R ap′=−R p′a=−1R 2dX a=−1R 2E aE p′. \begin{array}{l} R^{a_1 a_2} \;=\; - \tfrac{r^2}{R^4} \mathrm{d}X^{a_1}\, \mathrm{d}X^{a_2} \;=\; - \tfrac{1}{R^2} E^{a_1} \, E^{a_2} \\ R^{a p'} \,=\, - R^{p' a} \;=\; - \tfrac{1}{R^2} \mathrm{d}X^a \;=\; - \tfrac{1}{R^2} E^a \, E^{p'} \,. \end{array}

Hence the Riemann tensor has non-vanishing components

R a 1a 2 b 1b 2 = +1R 2δ b 1b 2 a 1a 2 R ap′ bp′ = +1R 2δ a b, \begin{array}{ccl} R^{a_1 a_2}{}_{b_1 b_2} &=& + \tfrac{1}{R^2} \delta^{a_1 a_2}_{b_1 b_2} \\ R^{a p'}{}_{b p'} &=& + \tfrac{1}{R^2} \delta^a{}_b \mathrlap{\,,} \end{array}

so that the Ricci tensor is proportional to the metric, as befits an Einstein manifold:

Ric a 1a 2 ≔ R a 1 b a 2b+R a 1 p′ a 2p′=pR 2η a 1a 2+1R 2η a 1a 2 = p+1R 2η a 1a 2 Ric p′p′ ≔ R p′ b p′b = p+1R 2. \begin{array}{ccl} Ric_{a_1 a_2} &\coloneqq& R_{a_1}{}^{b}{}_{a_2 b} \,+\, R_{a_1}{}^{p'}{}_{a_2 p'} \;=\; \tfrac{p}{R^2} \, \eta_{a_1 a_2} + \tfrac{1}{R^2} \, \eta_{a_1 a_2} \\ &=& \tfrac{p+1}{R^2} \, \eta_{a_1 a_2} \\ Ric_{p' p'} &\coloneqq& R_{p'}{}^b{}_{p' b} \\ &=& \tfrac{p+1}{R^2} \,. \end{array}

The above convention dE a=+Ω a bE b\mathrm{d}E^a = + \Omega^a{}_b \, E^b (4) makes this come out positive, following the old convention by Freund & Rubin 1980, see there.


Conformal boundary

(…) conformal boundary (…) [e.g. Frances 2011]

Holography

Asymptotically anti-de Sitter spaces play a central role in the realization of the holographic principle by AdS/CFT correspondence.

In pp-adic geometry

A 2-adic arithmetic geometry-version of AdS spacetime is identified with the Bruhat-Tits tree for the projective general linear group PGL(2,ℚ p)PGL(2,\mathbb{Q}_p):

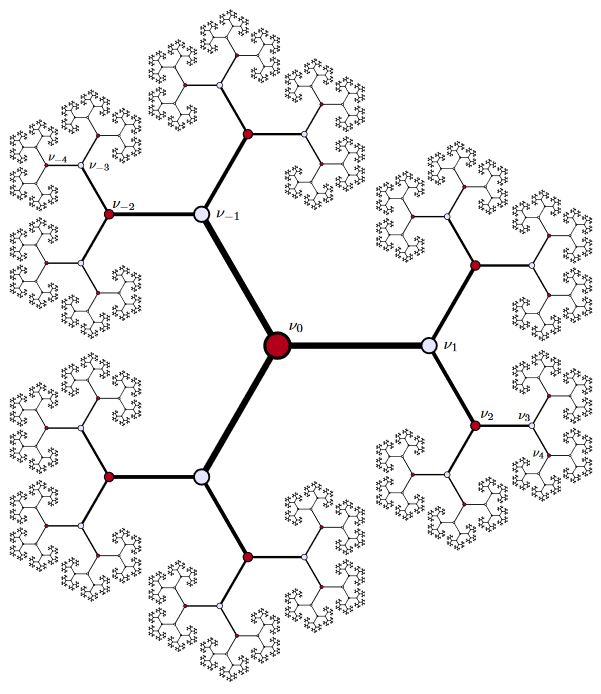
graphics from Casselman 14

In the p-adic AdS/CFT correspondence this may be regarded (at some finite depth truncation) as a tensor network state:

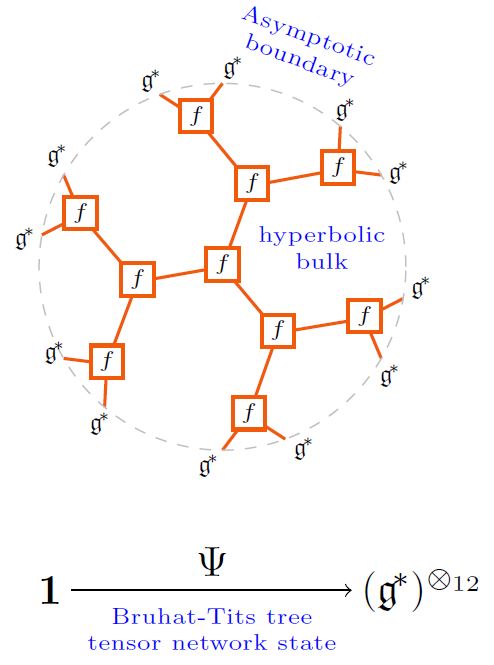
graphics from Sati-Schreiber 19c

and as such validates the Ryu-Takayanagi formula for holographic entanglement entropy.

References

Geometry

Review:

See also:

With attention to the conformal geometry:

Further discussion:

  • Abdelghani Zeghib, On closed anti de Sitter spacetimes, Math. Ann. 310, 695–716 (1998) (pdf)

  • Jiri Podolsky, Ondrej Hruska, Yet another family of diagonal metrics for de Sitter and anti-de Sitter spacetimes, Phys. Rev. D 95, 124052 (2017) (arXiv:1703.01367)

Quantum field theory

Discussion of (scalar) quantum field theory on AdS backgrounds:

Discussion of thermal Wick rotation on global anti-de Sitter spacetime (which is already periodic in real time) to Euclidean field theory with periodic imaginary time is in

Discussion of black holes in anti de Sitter spacetime:

  • Hawking, Stephen W., and Don N. Page. “Thermodynamics of black holes in anti-de Sitter space.” Communications in Mathematical Physics 87.4 (1983): 577-588.

  • M. Socolovsky, Schwarzschild Black Hole in Anti-De Sitter Space (arXiv:1711.02744)

  • Peng Zhao, Black Holes in Anti-de Sitter Spacetime (pdf)

  • Jakob Gath, The role of black holes in the AdS/CFT correspondence (pdf)

Relation to Teichmüller theory:

  • Francesco Bonsante, Andrea Seppi, Anti-de Sitter geometry and Teichmüller theory (arXiv:2004.14414)

Phenomenology

  • Anjan A. Sen, Shahnawaz A. Adil, Somasri Sen, Do cosmological observations allow a negative Λ\Lambda? (arXiv:2112.10641)

As string vacua

On (in-)stability of non-supersymmetric AdS vacua in string theory:

pp-Waves as Penrose limits of AdS p×S qAdS_p \times S^q spacetimes

Dedicated discussion of pp-wave spacetimes as Penrose limits (Inönü-Wigner contractions) of AdSp x S^q spacetimes and of the corresponding limit of AdS-CFT duality:

Review:

See also:

  • Michael Gutperle, Nicholas Klein, A Penrose limit for type IIB AdS 6AdS_6 solutions (arXiv:2105.10824)

Last revised on August 15, 2024 at 17:02:30. See the history of this page for a list of all contributions to it.

EditDiscussPrevious revisionChanges from previous revisionHistory (44 revisions) Cite Print Source