nLab computational trilogy
Context
Type theory
natural deduction metalanguage, practical foundations
type theory (dependent, intensional, observational type theory, homotopy type theory)
computational trinitarianism =
propositions as types +programs as proofs +relation type theory/category theory
Category theory
Concepts
Universal constructions
Theorems
Extensions
Applications
Constructivism, Realizability, Computability
constructive mathematics, realizability, computability
propositions as types, proofs as programs, computational trinitarianism
Constructive mathematics
Realizability
Computability
Contents
Idea
A profound cross-disciplinary insight has emerged – starting in the late 1970s, with core refinements in recent years – observing that three superficially different-looking fields of mathematics,
are but three different perspectives on a single underlying phenomenon at the foundations of mathematics:
Classical
Plain
Under the identifications
the following notions are equivalent:
| In intuitionistic logic and type theory: | In programming languages and computation: | In category theory and topos theory: |
|---|---|---|
| A proof of a proposition, or a term of some type. | A program/λ-term with output of some data type. | A generalized element of an object. |
whence these three subjects are but three perspectives on a single underlying phenomenon.
This insight dates from the late 1970s; an early record is Lambek & Scott 86; it is explicitly highlighted as a trilogy (Wikipedia: “three works of art that are connected and can be seen either as a single work or as three individual works”) in Melliès 06, Sec. 1:
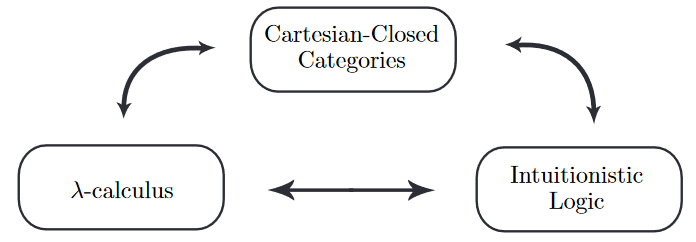
(Notice that Melliès 06 on p.2 does mean to regard λ-calculus as programming language.)
In Harper 11 the profoundness of the trilogy inspires the following emphatic prose, alluding to the doctrinal position of ‘trinitarianism’:
The central dogma of computational trinitarianism holds that Logic, Languages, and Categories are but three manifestations of one divine notion of computation. There is no preferred route to enlightenment: each aspect provides insights that comprise the experience of computation in our lives.
Computational trinitarianism entails that any concept arising in one aspect should have meaning from the perspective of the other two. If you arrive at an insight that has importance for logic, languages, and categories, then you may feel sure that you have elucidated an essential concept of computation–you have made an enduring scientific discovery.
For more detailed review see Eades 12, Sec. 3.
Parametrized
More is true: Since
-
computation happens in contexts and is proof relevant;
-
categories give rise to their systems of slice categories and are in general (∞,1)-categories;
-
types may depend on other types and are in general homotopy types
the traditional computational trilogy above enhances to read as follows:
| In dependent homotopy type theory: | In programming languages and computation: | In locally cartesian closed (∞,1)-categories/(∞,1)-toposes: |
|---|---|---|
| A term of some type in context. | A program outputting some data type in context. | A generalized element of an object in a slice. |
See also Shulman 18.
In this deeper form yet another equivalence – to algebraic topology (Sati Schreiber 20, p. 5) – opens up, as generalized elements in an (∞,1)-topos may equivalently be regarded as cocycles in (non-abelian) cohomology, and in twisted cohomology if in a slice (∞,1)-category (Sati Schreiber 20 p. 6, FSS 20), whence we have a computational tetralogy:
| In dependent homotopy type theory: | In programming languages and computation: | In locally cartesian closed ∞-categories/∞-toposes: | In non-abelian cohomology param. homotopy theory: |
|---|---|---|---|
| A term of some type in context. | A program of some data type in context. | An element of an object in a slice. | A cocycle in twisted cohomology. |
(graphics from SS22)
Quantum
Plain
An analogous trilogy is seen under passage:
-
from logic/type theory to linear logic/linear type theory;
-
from computation to quantum computation;
-
from cartesian closed categories to closed monoidal categories
This is the main point of Melliès 06, Sec. 1, only that where Melliès shows “proof nets” (p. 4) we refer to them as “quantum computation” for better emphasis, following Abramsky-Coecke 04, Abramsky & Duncan 05, Duncan 06; going back to Pratt 92:
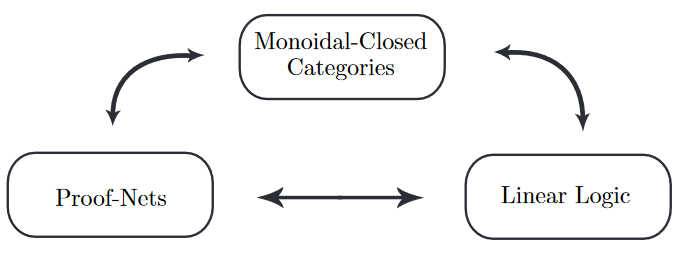
See also Baez & Stay 09.
Parametrized
Combining the classical parametrized trilogy with the plain quantum trilogy, as one passes
-
from classical computation to classically controlled quantum computation on linear spaces of quantum states parametrized over classical data types;
-
from dependent intuitionistic homotopy type theory to dependent linear type theory of dependent stable homotopy types;
-
from locally cartesian closed categories/(∞,1)-categories to indexed monoidal categories/(∞,1)-categories of parametrized spectra; which in the language of algebraic topology is the context of twisted generalized cohomology theory.
there appears the “classically controlled quantum computational tetralogy”:
(graphics from SS22)
| In dependent linear homotopy type theory: | In classically controlled quantum programming languages: | In indexed monoidal ∞-cats of par. spectra: | In Whitehead-generalized twisted cohomology theory: |
|---|---|---|---|
| A term of some type in context. | A quantum circuit controlled by classical data. | An element of an object in a slice. | A cocycle in twisted cohomology. |
(along the lines of Schreiber 14, Nuiten 13,
-
with parametrized stable homotopy theory understood as twisted cohomology theory as in Ando, Blumberg & Gepner 10, Ando, Blumberg, Gepner & Hopkins 14, Fiorenza, Sati, Schreiber 20;
-
with dependent linear homotopy type theory understood as, e.g., in Riley, Finster & Licata 21 following Schreiber 13 Prop. 4.1.9;
-
with classically controlled quantum computation seen as dependent linear type theory, as stated fully explicitly in Fu, Kishida & Selinger 20, Fu, Kishida, Ross & Selinger 20 and more tentatively before in Vakar 14, Vakar 15, Vakar 17, following Schreiber 14)
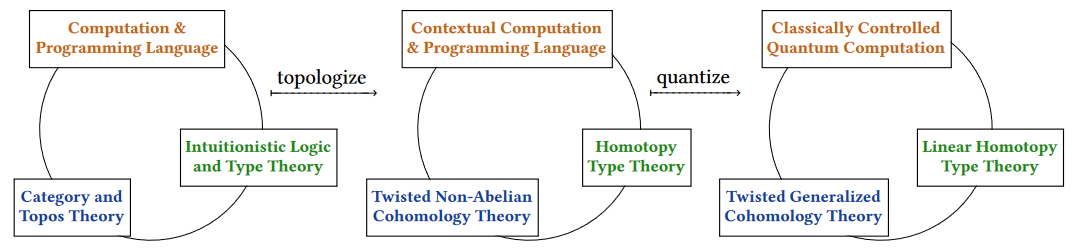
(from SS22)
Rosetta stone
The following shows a rosetta stone dictionary with more details:
(NB. This table shows the computational aspect mostly under “type theory”…)
computational trinitarianism =
propositions as types +programs as proofs +relation type theory/category theory
Related concepts
References
In the introduction of
- Paul-André Melliès, Functorial boxes in string diagrams, Procceding of Computer Science Logic 2006 in Szeged, Hungary. 2006 (hal:00154243, pdf, pdf)
the insight is recalled to have surfaced in the 1970s, with an early appearance in print being the monograph
- Joachim Lambek, Phil Scott, Introduction to Higher Order Categorical Logic, Cambridge Studies in Advanced Mathematics Vol. 7. Cambridge University Press, 1986 (ISBN:978-0-521-24665-1)
See also at History of categorical semantics of linear type theory for more on this.
A exposition of the relation between the three concepts is in
-
Robert Harper, The Holy Trinity (2011) (web, wayback machine snapshot)
-
Harley Eades, Section 3 of: Type Theory and Applications, 2012 (pdf, pdf)
-
Dan Frumin, Computational trinitarianism, Feb 2014 (prezi slides)
An exposition with emphasis on linear logic/quantum logic and the relation to physics is in
- John Baez, Mike Stay: Physics, Topology, Logic and Computation: A Rosetta Stone, in New Structures for Physics, Lecture Notes in Physics 813 Springer (2011) 95-174 [arXiv:0903.0340, doi:10.1007/978-3-642-12821-9_2]
Discussion in the context of homotopy type theory:
- Mike Shulman, Homotopical trinitarianism: A perspective on homotopy type theory, 2018 (pdf slides, pdf)
For further references see at programs as proofs, propositions as types, and relation between category theory and type theory.
Textbooks on the foundations of mathematics and foundations of programming language which connect via the common theme of type theory/categorical logic include the following:
-
William Lawvere, Robert Rosebrugh, Sets for Mathematics, Cambridge UP 2003 (book homepage, GoogleBooks, pdf)
-
Robert Harper, Practical Foundations for Programming Languages, Cambridge University Press (2016) (ISBN:9781107150300)
See also
- Joseph A. Goguen, A Categorical Manifesto. In Mathematical Structures in Computer Science 1 1 (1991) 49-67 (doi:10.1017/S0960129500000050, CiteSeerX.
Last revised on February 26, 2025 at 09:30:36. See the history of this page for a list of all contributions to it.