nLab equivariant Hopf degree theorem
Context
Homotopy theory
homotopy theory, (∞,1)-category theory, homotopy type theory
flavors: stable, equivariant, rational, p-adic, proper, geometric, cohesive, directed…
models: topological, simplicial, localic, …
see also algebraic topology
Introductions
Definitions
Paths and cylinders
Homotopy groups
Basic facts
Theorems
Representation theory
geometric representation theory
Ingredients
Definitions
representation, 2-representation, ∞-representation
Geometric representation theory
-
Grothendieck group, lambda-ring, symmetric function, formal group
-
principal bundle, torsor, vector bundle, Atiyah Lie algebroid
-
Eilenberg-Moore category, algebra over an operad, actegory, crossed module
Theorems
Contents
Idea
The equivariant Hopf degree theorem – Theorem below – generalizes the plain Hopf degree theorem from plain homotopy theory to equivariant homotopy theory, due to tomDieck 79, 8.4.
Preliminaries: Matching -Spaces
We need the following list of ingredients and assumptions:
Let be a finite group. For a subgroup, write
for its Weyl group.
For a G-space, we write
for the subset of the subgroup lattice on the isotropy groups of , hence those subgroups which appear as stabilizer subgroups of some point . This means that if and is a strict inclusion, then the fixed loci differ, .
Definition
(matching pair of -spaces)
For a finite group, we say that a pair of topological G-spaces, where is a G-CW-complex, is a matching pair if the following conditions are satisfied for all isotropy groups (2) of the -action on .
-
The fixed point space is a -complex of finite dimension ;
-
(integral cohomology of the fixed point space),
this implies that the action of on cohomology induces a group homomorphism
(3)to be called the orientation behaviour of the action of on ;
and
-
is -connected
(hence connected if , simply connected if , etc.);
-
(homotopy groups of fixed point space),
with the previous point this implies (by the Hurewicz theorem) that and hence orientation behaviour (3)
-
, the orientation behaviour (3) of and agrees at all isotropy groups.
For simplicity we also demand that
- .
Given a matching pair of -spaces, we say that a choice of generators in the cohomology groups of all the fixed strata
is a choice of singularity-wise orientations. Given such a choice and an equivariant continuous function , we have for each isotropy group that the continuous function has a well-defined integer degree
(tom Dieck 79, p. 212 and p. 213)
Example
(representation spheres match representation spheres)
Let be a finite group and a finite-dimensional orthogonal linear representation of . Then the pair
consisting of two copies of the representation sphere of is a matching pair of -spaces, according to Def. .
Proof
First notice that an -fixed locus of any -representation sphere is itself a -representation sphere, since . That these are all WH-CW-complexes follows because generally G-representation spheres are G-CW-complexes. Moreover, since the topological spaces underlying all these fixed loci are n-spheres, and since we have the same spheres for and , the connectivity and orientability conditions in Def. are evidently satisfied.
Example
(representation tori match representation spheres)
Let be a finite group which arises as the point group of a crystallographic group of some Euclidean space . Then the pair
consisting of
-
the torus which is the quotient space of by the given crystallographic sub-lattice and equipped with the -action descending from that on (this Prop.);
-
the representation sphere of the linear action of the point group on
Proof
The torus carries the structure of a smooth manifold for which the -action is smooth. Since is finite, also all its fixed loci are smooth manifolds (this Prop.). By the equivariant triangulation theorem, all these are WH-CW-complexes.
Moreover, the orientability and connectivity assumptions in Def. are evidently satisfied, using the fact that both as well as are modeled on the same linear -representation space .
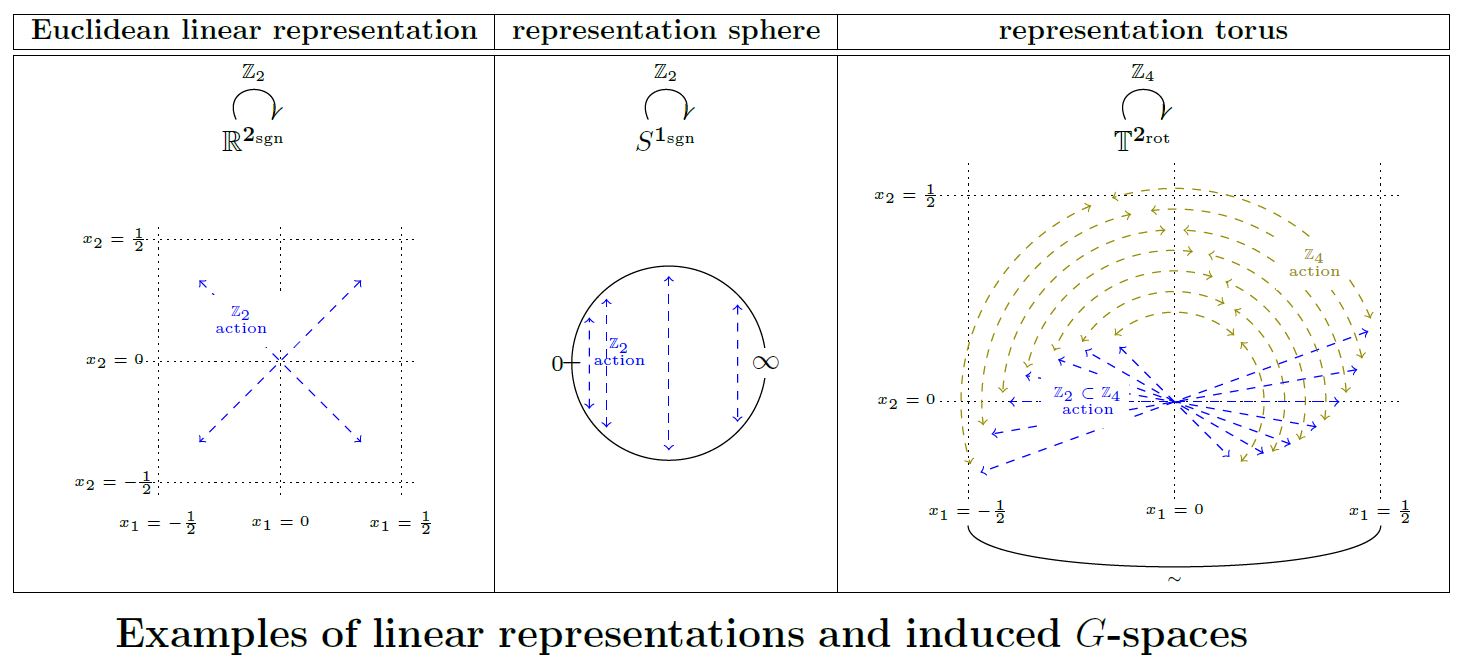
graphics grabbed from SS 19
Equivariant Hopf degree theorem
We first state the equivariant Hopf degree theorem for full (i.e. unstable/non-abelian) equivariant Cohomotopy, and then its stabilization to stable equivariant Cohomotopy.
In unstable equivariant Cohomotopy
Theorem
(equivariant Hopf degree theorem)
Given a matching pair of -spaces (Def. ) the function (from -equivariant homotopy classes to tuples of degrees labeled by isotropy groups) which sends any equivariant homotopy class of an equivariant continuous function to its -degrees (5)
is an injection.
Moreover, for each and for each
-
the -degree (5) modulo the order of the Weyl group
(6)is fixed by the degrees for all ;
-
there exists with specified degrees for and realizing any of the degrees allowed by the constraint (6).
In stable equivariant Cohomotopy
stabilization to stable equivariant Cohomotopy
(…)
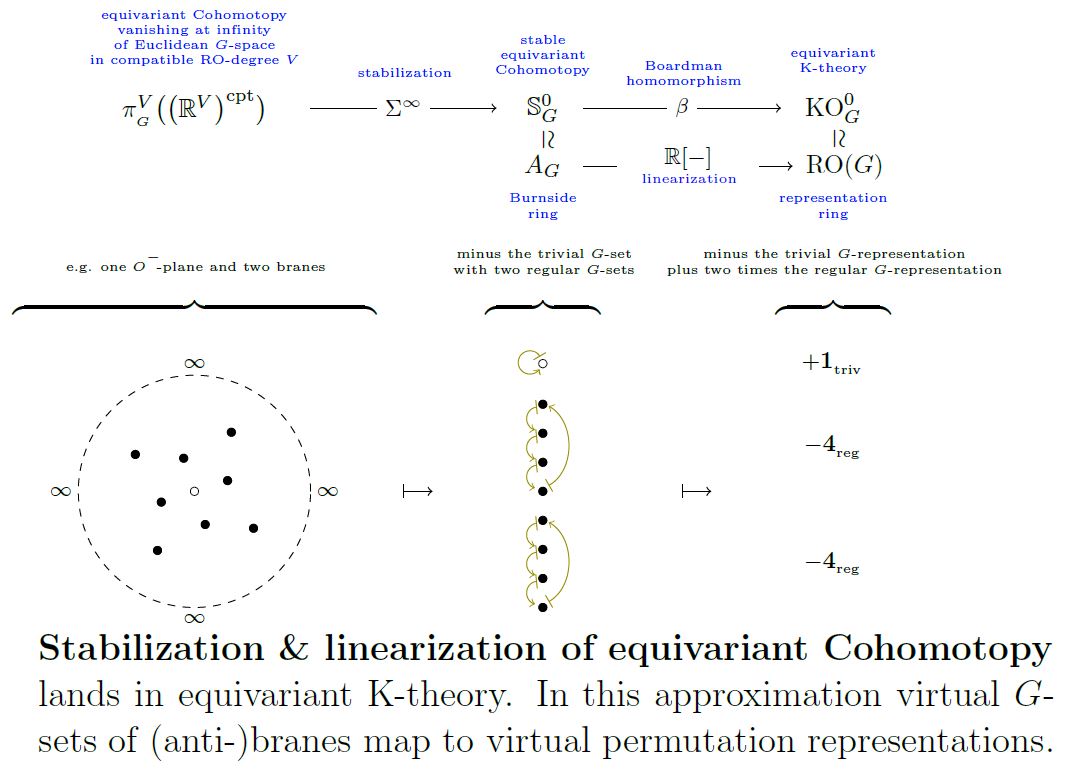
graphics grabbed from SS19
Examples
Equivariant Cohomotopy of representation spheres
As a special case of the equivariant Hopf degree theorem (Theorem ), we obtain the following:
Proposition
(equivariant cohomotopy of representation sphere in RO(G)-degree )
Let and . Then the pointed equivariant cohomotopy of the representation sphere in RO(G)-degree is the Cartesian product of one copy of the integers for each proper isotropy subgroup (2) in , and a copy of or depending on whether or not:
where on the right
is the winding number of the underlying continuous function of (co)restricted to -fixed points, and part of the claim is that in the cases with this is an integer multiple of the order of the Weyl group (1) up to an offset
which depends in a definite way on the degrees of for all isotropy groups .
Proof
This follows as a special case of the equivariant Hopf degree theorem (Theorem ).
Here is a matching pair of -spaces according to Example .
This equivariant Hopf degree theorem is stated above under the simplifying assumption that the dimension of all fixed loci is positive. But the proof from tomDieck 79, 8.4 immediately applies to our situation where the dimension of the fixed locus at the full subgroup may be 0, with . This gives a choice in in the first step of the inductive argument in tomDieck 79, 8.4, and from there on the proof applies verbatim.
Alternatively, if we may consider maps which restrict on to degree zero or one.
Example
(equivariant cohomotopy of in RO(G)-degree the sign representation )
Let the cyclic group of order 2 and its 1-dimensional sign representation.
Under equivariant stereographic projection (here) the corresponding representation sphere is equivalently the unit circle
equipped with the -action whose involution element reflects one of the two coordinates of the ambient Cartesian space
Equivalently, if we identify
then the involution action is
This means that the fixed point space is the 0-sphere
being two antipodal points on the circle, which in the presentation (7) are labeled .
Notice that the map
of constant parameter speed and winding number is equivariant for this -action on both sides:
Now the restriction of the map from (8) to the fixed points
sends (0 to 0 and) to either or to , depending on whether the winding number is odd or even:
Hence if the restriction to the fixed locus is taken to be the identity (bipointed equivariant cohomotopy) then, in accord with Prop. there remains the integers worth of equivariant homotopy classes, where each integer corresponds to the odd winding integer
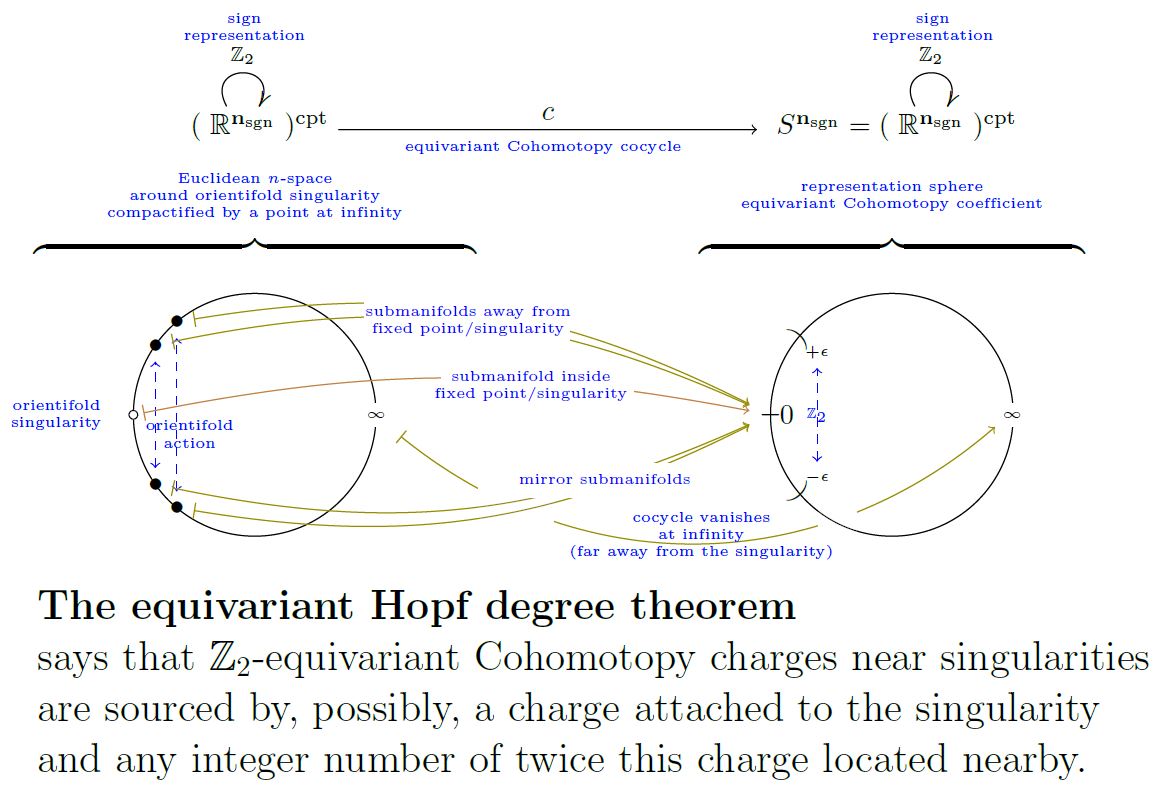
graphics grabbed form Sati-Schreiber 19
Remark
This result
becomes, after stabilization to equivariant stable homotopy theory, the stable homotopy groups of the equivariant sphere spectrum in RO(G)-grading given by
see there.
Example
(equivariant cohomotopy of in RO(G)-degree the quaternions )
Let be a non-trivial finite subgroup of SU(2) and let be the real vector space of quaternions regarded as a linear representation of by left multiplication with unit quaternions.
Then the bi-pointed equivariant cohomotopy of the representation sphere in RO(G)-degree is
Proof
The only isotropy subgroups of the left action of on are the two extreme cases . Hence the only multiplicity that appears in Prop. is
and all degrees must differ from that of the class of the identity function by a multiple of this multiplicity. Finally, the offset of the identity function is clearly .
Equivariant Cohomotopy of representation tori
For the case of representation tori
(…)
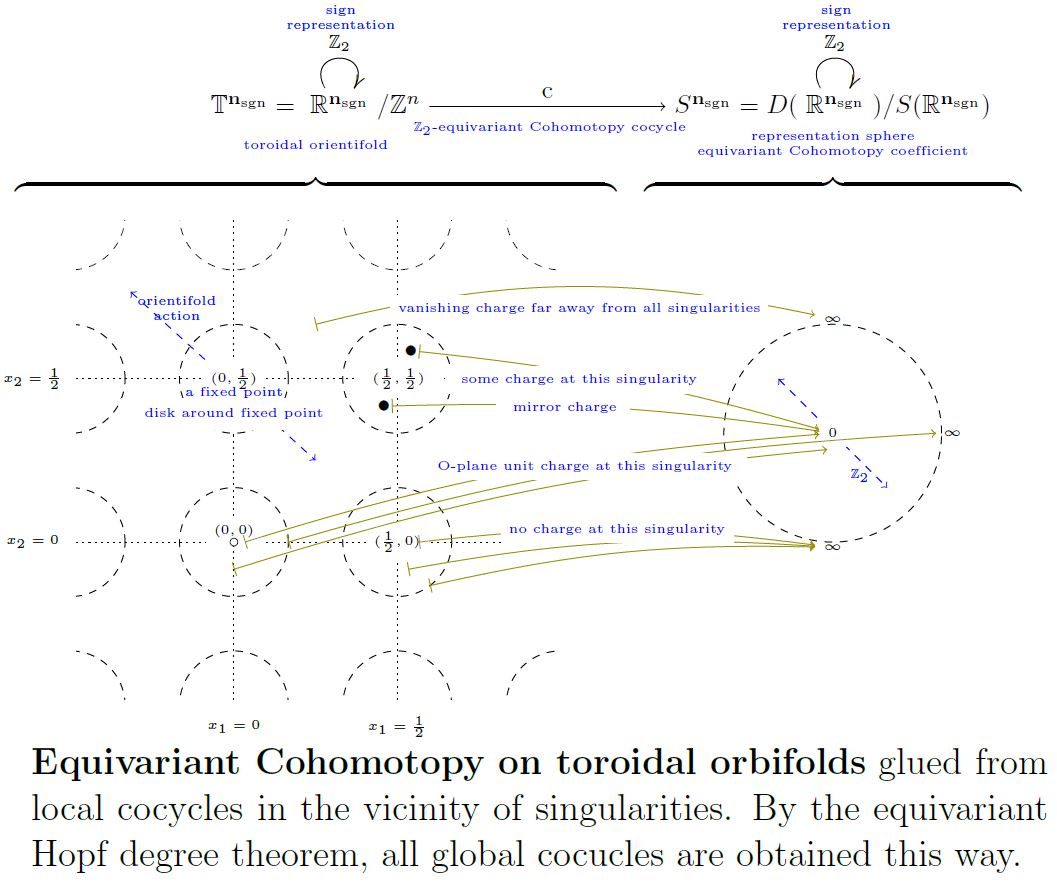
graphics grabbed form Sati-Schreiber 19
Related concepts
References
Discussion of equivariant maps between suitable matching pairs of -spaces is in
-
Tammo tom Dieck, Section 8.4 of: Transformation Groups and Representation Theory, Lecture Notes in Mathematics 766 Springer 1979
-
Tammo tom Dieck, Section II.4 of: Transformation Groups, de Gruyter 1987 (doi:10.1515/9783110858372)
Discussion specifically for the codomain a representation sphere (i.e. for equivariant cohomotopy):
-
Zalman Balanov, Equivariant Hopf theorem, Nonlinear Analysis: Theory, Methods & Applications Volume 30, Issue 6, December 1997, Pages 3463-3474 (doi:10.1016/S0362-546X(97)00020-5)
-
Davide L. Ferrario, On the equivariant Hopf theorem, Topology Volume 42, Issue 2, March 2003, Pages 447-465 (doi:10.1016/S0040-9383(02)00015-0)
-
Markus Szymik, A stable approach to the equivariant Hopf theorem (pdf, pdf)
The above discussion follows
- Hisham Sati, Urs Schreiber, Equivariant Cohomotopy implies orientifold tadpole cancellation (arXiv:1909.12277)
which applies equivariant Cohomotopy to RR-field tadpole cancellation.
Last revised on July 16, 2025 at 17:40:54. See the history of this page for a list of all contributions to it.