nLab RR-field tadpole cancellation
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
- Idea
- In plane and toroidal orientifolds
- In terms of equivariant K-theory / the representation ring
- Examples for toroidal orientifolds
- Examples of non-compact singularities
- At a -orientifold singularity
- At a -orientifold singularity
- At a -orientifold singularity
- At a -orientifold singularity
- At a -orientifold singularity
- At a -orientifold singularity
- At a -orientifold singularity
- At a -orientifold singularity
- At a -orientifold singularity
- At a -orientifold singularity
- At a -orientifold singularity
- At a -orientifold singularity
- Related concepts
- References
Idea
In the presence of D-branes, plain type II string theory in fact has a quantum anomaly reflected on the worldsheet by tadpole Feynman diagrams in the string perturbation series for RR-fields
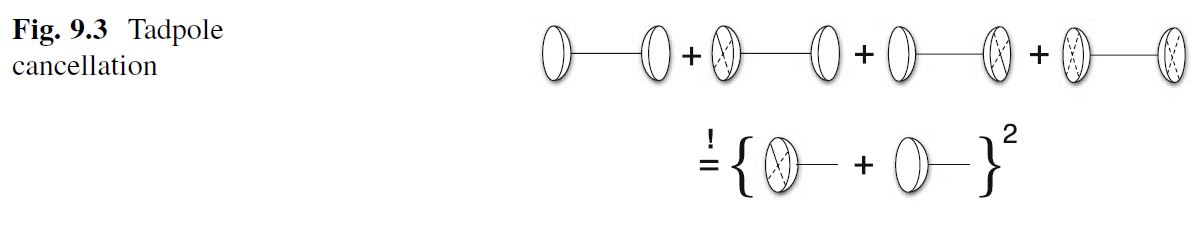
graphics grabbed from Blumenhagen-Lüst-Theisen 13
and reflected in target spacetime by non-trivial total RR-field flux on compact spaces

graphics grabbed from Ibanez-Uranga 12
This anomaly cancels if the D-branes are accompanied by a suitable collection of O-planes, hence if one considers orientifold backgrounds (Sagnotti 88, pp. 5, Gimon-Polchinski 96, section 3). (For space-filling O-planes this means to consider type I string theory instead.)
Accordingly, tadpole cancellation via orientifolding is a key consistency condition in the construction of intersecting D-brane models for string phenomenology.
Traditionally RR-tadpole cancellation is discussed in ordinary cohomology, the common arguments notwithstanding that D-brane charge should be in K-theory.
Discussion of tadpole cancellation with D-brane charge regarded in K-theory was initated in Uranga 00, Section 5, see also Garcia-Uranga 05, Marchesano 03, Section 4, Marchesano-Shiu 04, CKMNW 05, Section 2.2, Maiden-Shiu-Stefanski 06, Section 5, DFM 09, p. 6-7.
But the situation remains somewhat inconclusive (see also Moore 14, p. 21-22).
In plane and toroidal orientifolds
More details are understood in the special case of plane orbifolds and toroidal orientifolds where fractional D-branes may be stuck at orbifold/orientifold singularities, whose D-brane charge is supposed to be in the equivariant K-theory of the point, hence the representation ring of the given isotropy group.
In terms of equivariant K-theory / the representation ring
In this case tadpole cancellation conditions are given by representation theoretic equations, constraining the characters of the linear representations corresponding to the fractional D-branes.
Let be a finite group. Let
be a linear extension of its partially ordered lattice of conjugacy classes of subgroups, with sub- linear order of cyclic subgroups
This way every virtual representation (the D-brane charge of a bound state of fractional D-branes/anti-branes) has a character which is a list of complex numbers of the form
Here is the mass, hence the net number of fractional D-branes/anti-branes in the bound state, while is (up to a global rational number-factor ) supposed to be its charge as seen by the RR-fields in the -twisted sector.
In fact, since we are dealing with fractional D-branes, both the charge and mass in the above table are in factional units of the order of the isotropy group (by this formula), so that normalized mass and charge is
Local/twisted tadpole cancellation
The twisted (local) tadpole cancellation condition for fractional D-branes at orbifold singularities is that the RR-charges in all non-trivially twisted sectors vanish:
Example
(regular representation solves tadpole cancellation for fractional D-branes)
For every finite group , the homogeous tadpole cancellation condition (2) is satisfied by all multiples of the regular representation (since no non-trivial element has fixed points when acting on , and using this Prop.). Hence the mass and charge (1) of the fractional D-brane corresponding to the regular representation is
These multiples of the regular representation are regarded as trivial solutions to (2).
Proposition
In fact, the multiples of the regular representation (Example ) are the only solutions to the local/twisted tadpole cancellation condition (2) for fractional D-branes.
Proof
Consider the truncated character morphism
We have to show that the kernel of this map is the free abelian group generated by the regular representation:
Now over a ground field of characteristic zero (such as the real numbers or complex numbers, in the case at hand) we have (from this Example) that
-
for a non-trivial irreducible representation we have
-
for the trivial irreducible representation we have
Since every is a -linear combination of these irreps, it follows generally that the fractional part of the mass of a fractional D-brane is recovered from its charges:
But this means that all in the kernel of must have
This is indeed the case for the multiples of the regular representation (Example ). Conversely, the injectivity of the full character morphism (this Prop.) says that every with and must be the th multiple of the regular representation.
Global/untwisted tadpole cancellation
On the other hand, at an orientifold singularity, the O-plane itself carries such charge – O-plane charge (see there):
(These are -plane charges. There may also be -plane charges. Alternatively, these are -branes with a fractional D-brane stuck on them.)
Now the untwisted (global) tadpole cancellation condition is that (all representations are real and) this O-plane charge is cancelled against the D-brane charge:
By Prop. the only possible solution of this is the th multiple of the regular representation, if is times the dimension of the regular representation:
In basic examples the O-plane-charge
is for coincident O-planes is the corresponding multiple by the O-plane charge (here) of the trivial irrep, whence a solution to the tadpole cancellation exists if and is then given by
Sometimes the condition (5) is found with an offset by a trivial representation
This corresponds to single fractional D-branes sitting on top of the O-planes, turning -planes into -planes.
Examples for toroidal orientifolds
RR-field tadpole cancellation conditions for D-branes wrapped on toroidal orientifolds
in terms of their D-brane charge in equivariant K-theory = representation ring
(here denotes the regular representation of dimension ord(G))
| single D-brane species on toroidal orientifold | local/twisted tadpole cancellation condition | global/untwisted tadpole cancellation condition | comment |
|---|---|---|---|
| D5-branes transv. to | (Buchel-Shiu-Tye 99 (19)) | (Buchel-Shiu-Tye 99 (18)) | following Gimon-Polchinski 96, Gimon-Johnson 96 |
| D5-branes transv. to | (Buchel-Shiu-Tye 99 (19)) | (Buchel-Shiu-Tye 99 (18)) | following Gimon-Polchinski 96, Gimon-Johnson 96 |
| D4-branes transv. to | (AFIRU 00a, 4.2.1) | ||
| D4-branes transv. to | (AFIRU 00b, (7.2)) | (Kataoka-Shimojo 01, (14)-(17) | |
| D8-branes on | | (Honecker 01, 4, Honecker 02a, (25) ∧ (28) ⇔ (29), Honecker 02b, (3.19)-(3.27)) | equivalent to D4 case by T-duality: Honecker 01, p. 2, Honecker 02a, 6, Honecker 02b, p. 15 review in: Marchesano 03, Sec. 4 |
| D6-branes on | (Ishihara-Kataoka-Sato 99, (4.16)) | ||
| D3-branes on | (Feng-He-Karch-Uranga 01, (25)) | ||
| D7-branes on | (Feng-He-Karch-Uranga 01, (5), (6)) |
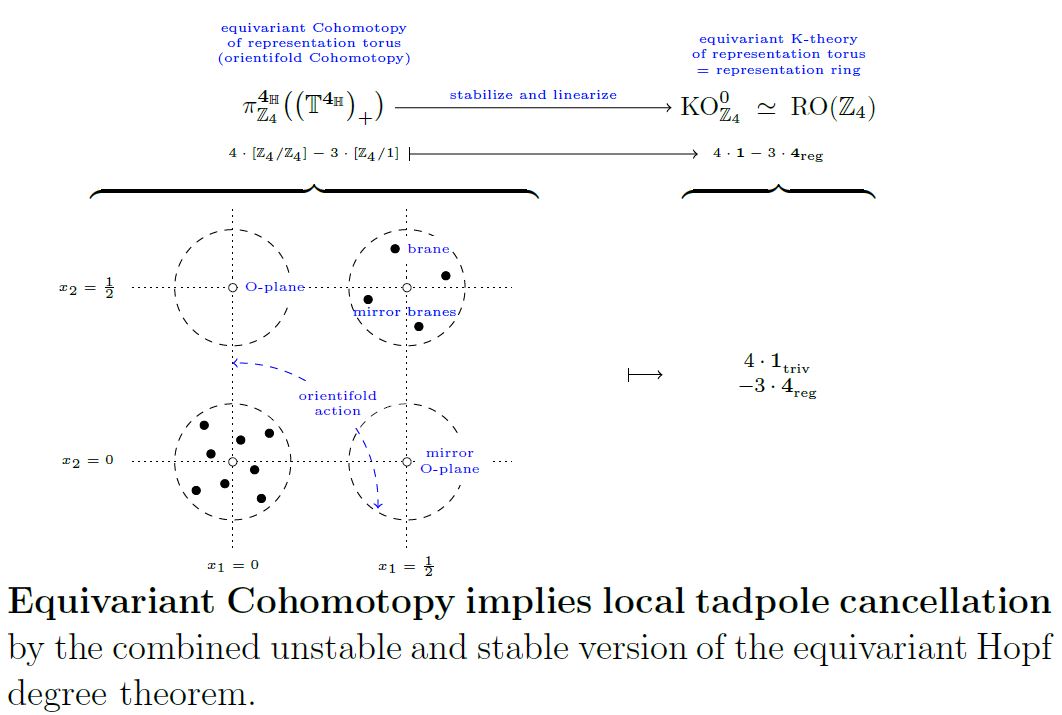
graphics grabbed from Sati-Schreiber 19
See also at equivariant Hopf degree theorem.

graphics grabbed from Sati-Schreiber 19
Examples of non-compact singularities
We discuss more explicitly the solutions to the local/twisted tadpole cancellation condition (2) for fractional D-branes at orbifold singularities for isotropy group one of the non-abelian finite subgroups of SU(2),
hence those in the D- and E-series, hence the binary dihedral groups and the three exceptional cases: 2T, 2O and 2I.
For these groups, by BSS 18, Theorem 4.1 the virtual permutation representations span precisely the sub charge lattice of integral (non-irrational) characters/RR-charges in the orientifold charge lattice of the corresponding ADE-singularity, namely of the equivariant KO-theory=real representation ring
Since the tadpole cancellation condition (2) in particular requires the characters/charges to be integral (specifically: zero) the general solution to the tadpole cancellation condition is indeed in this sub-lattice, and so that is where we may and do solve it, below.
In accord with the general Prop. we find that in each case there is precisely a 1-dimensional (i.e. ) sublattice of the charge lattice (the representation ring) which solves the twisted tadpole cancellation condition (2), hence a sublattice given by the integer-multiples of one single fractional D-brane bound state . There are then necessarily two of these generators . We check below that in all cases the normalized mass of these is unity, as it must be for the regular representation, by Prop. .
At a -orientifold singularity
For the cyclic group of order , the characters/D-brane charges of the elementary virtual permutation representations/fractional D-branes are (e.g. here)
One sees immediately that the general solution to the local/twisted tadpole cancellation condition (2) for is
whose minimal positive mass (net brane number) is
At a -orientifold singularity
For the cyclic group of order 4, the characters/D-brane charges of the complex irreducible representations/fractional D-branes are (e.g. here)
One sees immediately that the general solution to the local/twisted tadpole cancellation condition (2) for is
whose minimal positive mass (net brane number) is
At a -orientifold singularity
For the binary dihedral group of order (equivalently: the quaternion group), the characters/D-brane charges of the elementary virtual permutation representations/fractional D-branes are (BSS 18, 4.1):
One sees (here) that the general solution to the local/twisted tadpole cancellation condition (2) for is
whose minimal positive mass (net brane number) is
At a -orientifold singularity
For the binary dihedral group of order , the characters/D-brane charges of the elementary virtual permutation representations/fractional D-branes are (BSS 18, 4.2):
One finds (here) that the general solution to the local/twisted tadpole cancellation condition (2) for is
whose minimal positive mass (net brane number) is
At a -orientifold singularity
For the binary dihedral group of order , the characters/D-brane charges of the elementary virtual permutation representations/fractional D-branes are (BSS 18, 4.3):
One finds (here), that the general solution to the local/twisted tadpole cancellation condition (2) for is
whose minimal positive mass (net brane number) is
At a -orientifold singularity
For the binary dihedral group of order , the characters/D-brane charges of the elementary virtual permutation representations/fractional D-branes are (BSS 18, 4.4):
One finds (here) that the general solution to the local/twisted tadpole cancellation condition (2) for is
whose minimal positive mass (net brane number) is
At a -orientifold singularity
For the binary dihedral group of order , the characters/D-brane charges of the elementary virtual permutation representations/fractional D-branes are (BSS 18, 4.5):
One sees (here) that the general solution to the local/twisted tadpole cancellation condition (2) for is
whose minimal positive mass (net brane number) is
At a -orientifold singularity
For the binary dihedral group of order , the characters/D-brane charges of the elementary virtual permutation representations/fractional D-branes are (BSS 18, 4.6):
One sees by immediate inspection, that the general solution to the local/twisted tadpole cancellation condition (2) for is
whose minimal positive mass (net brane number) is
At a -orientifold singularity
For the binary dihedral group of order , the characters/D-brane charges of the elementary virtual permutation representations/fractional D-branes are (BSS 18, 4.7):
One sees by immediate inspection, that the general solution to the local/twisted tadpole cancellation condition (2) for is
whose minimal positive mass (net brane number) is
At a -orientifold singularity
For the binary tetrahedral group (whose order is ), the characters/D-brane charges of the elementary virtual permutation representations/fractional D-branes are (BSS 18, 4.8):
One finds (here) that the general solution to the local/twisted tadpole cancellation condition (2) for is
whose minimal positive mass (net brane number) is
At a -orientifold singularity
For the binary octahedral group (whose order is ), the characters/D-brane charges of the elementary virtual permutation representations/fractional D-branes are (BSS 18, 4.9):
One finds (here) that the general solution to the local/twisted tadpole cancellation condition (2) for is
whose minimal positive mass (net brane number) is
At a -orientifold singularity
For the binary icosahedral group (whose order is ), the characters/D-brane charges of the elementary virtual permutation representations/fractional D-branes are (BSS 18, 4.10):
One finds (here) that the general solution to the local/twisted tadpole cancellation condition (2) for is
whose minimal positive mass (net brane number) is
Related concepts
References
General
The issue was first highlighted in
- Augusto Sagnotti, Open strings and their symmetry groups in G. Mack et. al. (eds.) Cargese ’87, “Non-perturbative Quantum Field Theory,” (Pergamon Press, 1988) p. 521 (arXiv:hep-th/0208020)
The argument is recalled in
- Eric Gimon, Joseph Polchinski, section 3 of Consistency Conditions for Orientifolds and D-Manifolds, Phys.Rev.D54:1667-1676, 1996 (arXiv:hep-th/9601038)
Details are in
- Edward Witten, section 9.3 of Superstring Perturbation Theory Revisited (arXiv:1209.5461)
Textbook accounts include
-
Luis Ibáñez, Angel Uranga, section 4.4 of String Theory and Particle Physics – An Introduction to String Phenomenology, Cambridge 2012
-
Ralph Blumenhagen, Dieter Lüst, Stefan Theisen, section 9.4 of Basic Concepts of String Theory Part of the series Theoretical and Mathematical Physics, Springer 2013
Quick illustrations include:
Critical outlook in
- Gregory Moore p. 21-22 of Physical Mathematics and the Future, talk at Strings 2014 (talk slides, companion text pdf, pdf)
The above discussion follows and character tables for virtual permutation representations above are taken from
-
Simon Burton, Hisham Sati, Urs Schreiber, Lift of fractional D-brane charge to equivariant Cohomotopy theory, Journal of Geometry and Physics 161 (2021) 104034 [arXiv:1812.09679, Python code, doi:10.1016/j.geomphys.2020.104034]
-
Hisham Sati, Urs Schreiber, Equivariant Cohomotopy implies orientifold tadpole cancellation, Journal of Geometry and Physics 156 (2020) 103775 [arXiv:1909.12277, doi:10.1016/j.geomphys.2020.103775]
See also
-
G. Aldazabal, D. Badagnani, Luis Ibáñez, Angel Uranga, Tadpole versus anomaly cancellation in compact IIB orientifolds, JHEP 9906:031, 1999 (arXiv:hep-th/9904071)
-
Angel Uranga, D-brane probes, RR tadpole cancellation and K-theory charge, Nucl.Phys.B598:225-246, 2001 (arXiv:hep-th/0011048)
-
Maria E. Angulo, David Bailin, Huan-Xiong Yang, Tadpole and Anomaly Cancellation Conditions in D-brane Orbifold Models, Int.J.Mod.Phys.A18:3637-3694, 2003 (arXiv:hep-th/0210150)
-
Fernando Marchesano, section 4 of Intersecting D-brane Models (arXiv:hep-th/0307252)
-
Fernando Marchesano, Gary Shiu, Building MSSM Flux Vacua, JHEP0411:041, 2004 (arXiv:hep-th/0409132)
-
C.-M. Chen, G. V. Kraniotis, V. E. Mayes, D. V. Nanopoulos, J. W. Walker, A K-theory Anomaly Free Supersymmetric Flipped SU(5) Model from Intersecting Branes, Phys.Lett. B625 (2005) 96-105 (arXiv:hep-th/0507232)
-
Inaki Garcia-Etxebarria, Angel Uranga, From F/M-theory to K-theory and back, JHEP 0602:008, 2006 (arXiv:hep-th/0510073)
-
John Maiden, Gary Shiu, Bogdan Stefanski, D-brane Spectrum and K-theory Constraints of D=4, N=1 Orientifolds, JHEP0604:052,2006 (arXiv:hep-th/0602038)
-
Tetsuji Kimura, Mitsuhisa Ohta, Kei-Jiro Takahashi, Type IIA orientifolds and orbifolds on non-factorizable tori, Nucl. Phys. B 798 (2008) 89-123 [arXiv:0712.2281, doi:10.1016/j.nuclphysb.2008.01.030]
-
Jacques Distler, Dan Freed, Greg Moore, Orientifold Précis in: Hisham Sati, Urs Schreiber (eds.) Mathematical Foundations of Quantum Field and Perturbative String Theory, Proceedings of Symposia in Pure Mathematics, AMS (2011) (arXiv:0906.0795, slides)
In view of consistency of flux compactifications:
- Philip Betzler, Erik Plauschinn, Type IIB flux vacua and tadpole cancellation (arXiv:1905.08823)
For the topological string:
- Johannes Walcher, Evidence for Tadpole Cancellation in the Topological String, Communications in Number Theory and Physics 3 1 (2009) [arXiv:0712.2775]
Examples and Models
Specifically K3 orientifolds () in type IIB string theory, hence for D9-branes and D5-branes:
-
Eric Gimon, Joseph Polchinski, Section 3.2 of: Consistency Conditions for Orientifolds and D-Manifolds, Phys. Rev. D54: 1667-1676, 1996 (arXiv:hep-th/9601038)
-
Eric Gimon, Clifford Johnson, K3 Orientifolds, Nucl. Phys. B477: 715-745, 1996 (arXiv:hep-th/9604129)
-
Alex Buchel, Gary Shiu, S.-H. Henry Tye, Anomaly Cancelations in Orientifolds with Quantized B Flux, Nucl.Phys. B569 (2000) 329-361 (arXiv:hep-th/9907203)
-
P. Anastasopoulos, A. B. Hammou, A Classification of Toroidal Orientifold Models, Nucl. Phys. B729:49-78, 2005 (arXiv:hep-th/0503044)
Specifically K3 orientifolds () in type IIA string theory, hence for D8-branes and D4-branes:
-
J. Park, Angel Uranga, A Note on Superconformal N=2 theories and Orientifolds, Nucl. Phys. B542:139-156, 1999 (arXiv:hep-th/9808161)
-
G. Aldazabal, S. Franco, Luis Ibanez, R. Rabadan, Angel Uranga, D=4 Chiral String Compactifications from Intersecting Branes, J. Math. Phys. 42:3103-3126, 2001 (arXiv:hep-th/0011073)
-
G. Aldazabal, S. Franco, Luis Ibanez, R. Rabadan, Angel Uranga, Intersecting Brane Worlds, JHEP 0102:047, 2001 (arXiv:hep-ph/0011132)
-
H. Kataoka, M. Shimojo, Chiral Models from Intersecting D4-/D5-branes, Progress of Theoretical Physics, Volume 107, Issue 6, June 2002, Pages 1291–1296 (arXiv:hep-th/0112247, doi:10.1143/PTP.107.1291)
The action with even contains an order 2 element Then there will be D8-branes in the type IIA D4-brane theory. Since the concept of intersecting D-branesinvolves use of the same dimensional D-branes, we restrict ourselves to the case that the order of is odd. (p. 4)
-
Gabriele Honecker, Non-supersymmetric Orientifolds with D-branes at Angles, Fortsch.Phys. 50 (2002) 896-902 (arXiv:hep-th/0112174)
-
Gabriele Honecker, Intersecting brane world models from D8-branes on type IIA orientifolds, JHEP 0201 (2002) 025 (arXiv:hep-th/0201037)
-
Gabriele Honecker, Non-supersymmetric orientifolds and chiral fermions from intersecting D6- and D8-branes, thesis 2002 (pdf)
The Witten-Sakai-Sugimoto model on D4-D8-brane bound states for QCD with orthogonal gauge groups on O-planes:
-
Toshiya Imoto, Tadakatsu Sakai, Shigeki Sugimoto, and QCD from String Theory, Prog.Theor.Phys.122:1433-1453, 2010 (arXiv:0907.2968)
-
Hee-Cheol Kim, Sung-Soo Kim, Kimyeong Lee, 5-dim Superconformal Index with Enhanced Global Symmetry, JHEP 1210 (2012) 142 (arXiv:1206.6781)
Specifically D5 brane models T-dual to D6/D8 models:
-
Angel Uranga, A New Orientifold of and Six-dimensional RG Fixed Points, Nucl. Phys. B577:73-87, 2000 (arXiv:hep-th/9910155)
-
Bo Feng, Yang-Hui He, Andreas Karch, Angel Uranga, Orientifold dual for stuck NS5 branes, JHEP 0106:065, 2001 (arXiv:hep-th/0103177)
Specifically for D6-branes:
-
S. Ishihara, H. Kataoka, Hikaru Sato, , , Type IIA Orientifolds, Phys. Rev. D60 (1999) 126005 (arXiv:hep-th/9908017)
-
Mirjam Cvetic, Paul Langacker, Tianjun Li, Tao Liu, D6-brane Splitting on Type IIA Orientifolds, Nucl. Phys. B709:241-266, 2005 (arXiv:hep-th/0407178)
Specifically for D3-branes/D7-branes:
Various:
- Dieter Lüst, S. Reffert, E. Scheidegger, S. Stieberger, Resolved Toroidal Orbifolds and their Orientifolds, Adv.Theor.Math.Phys.12:67-183, 2008 (arXiv:hep-th/0609014)
Last revised on January 4, 2024 at 08:57:09. See the history of this page for a list of all contributions to it.